一个解非光滑方程组的Levenberg-Marquardt算法*

郑玲爱， 凌 晨

(杭州电子科技大学 运筹与控制研究所，浙江 杭州 310018)

一个解非光滑方程组的Levenberg-Marquardt算法*

郑玲爱， 凌 晨

(杭州电子科技大学 运筹与控制研究所，浙江 杭州 310018)

给出了一个求解非光滑约束方程组的Levenberg-Marquardt算法，每一步迭代中只需求解一个严格凸的二次规划问题.首先，利用松弛变量的绝对值函数将原问题转化成一个无约束方程组；然后，结合光滑化技术设计Levenberg-Marquardt算法.此算法具有全局收敛性，并且在弱于非奇异性的局部误差界条件下，具有局部二次收敛性质.初步的数值试验结果表明，此算法实际计算效果良好.

约束方程组；光滑化技术；Levenberg-Marquardt算法；强半光滑性；收敛性

0 引 言

研究如下非光滑约束方程组的数值求解问题:

式(1)中:X={x∈Rn|h(x)≤0};F:X→Rp和h:Rn→Rm均在某一包含X的开集上局部Lipschitz连续.约束方程组有广泛应用，许多重要问题(例如非线性互补、变分不等式、半无限规划)都可以转化成形如式(1)的问题[1-3].传统的Levenberg-Marquardt算法是求解光滑(即连续可微)无约束方程组的经典、有效方法之一.文献[4-5]已经证明，在局部误差界条件下，Levenberg-Marquardt算法具有局部二次收敛性质.求解约束方程组的一类典型方法是将问题转化为一个约束规划问题，并运用标准的优化算法解之[6-7].特别地，若F(5)非光滑但‖F(5)‖2光滑，且可行域X可表示为盒子约束，则已有一些行之有效的算法[8].然而，因问题(1)中X和相关效益函数都有可能为非凸，函数‖F(5)‖2和h(5)均不光滑，方程个数与未知量个数也未必相等，所以许多算法不能直接被应用.

本文给出一个求解问题(1)的光滑化Levenberg-Marquardt算法.此算法在每一步迭代中只需求解一个严格凸的二次规划问题,不仅具有全局收敛性质，而且在弱于非奇异性的局部误差界条件下具有局部二次收敛性.数值试验结果显示该算法效果良好.

1 光滑化函数

利用松弛变量的绝对值函数将问题(1)转化成一个无约束方程组，即

式(2)中:y=(x,t)∈Rn×Rm;|t|=(|t1|,|t2|,…,|tm|)T.显然，当且仅当方程(1)的解集X*≠Ø时，方程(2)的解集Y*≠Ø.进一步，若y*=(x*,t*)是方程(2)的解，则x*是方程(1)的解.为克服函数F(5),h(5)和|5|的非光滑性给算法设计带来的困难，特引进它们的光滑化逼近函数，并讨论相关的性质.

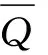
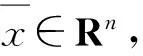
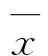
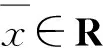
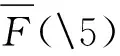
其解集记为Z*.关于问题(2)，给出如下局部误差界条件:

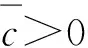
针对函数H，易证以下命题成立:

命题1设条件1成立,则对任意z*∈Z*，存在常数c1>0和邻域N(z*,δ1):={z∈R1+n+m| ‖z-z*‖≤δ1,ε≥0}，使得对任意z∈N(z*,δ1)，有

2 一个光滑化Levenberg-Marquardt算法

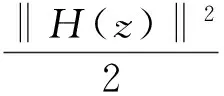
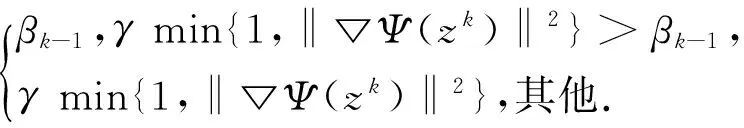
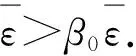
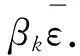
进一步易知，若zk不是Ψ(5)的稳定点，则相应的拉格朗日乘子αk必定唯一.

算法1：

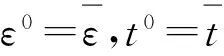
第1步：若zk满足终止条件，则停止.否则，由式(7)和式(8)计算βk.

第2步：解方程(9)，得dk=(dkε,dkx,dkt)T.

第3步：若‖H(zk+dk)‖≤γ‖H(zk)‖，则令zk+1:=zk+dk；否则，记mk为满足

的最小非负整数，令zk+1:=zk+ρmkdk.

第4步：令μk+1=‖H(zk+1)‖τ和k:=k+1，并转至第1步.

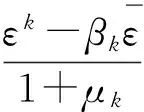
关于算法1，有如下命题:

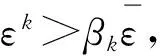
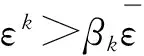
证明 由命题2和3即可证得.证毕.

3 收敛性分析

为确保算法1具有全局收敛性，给出如下条件：

条件2方程组(1)的解集X*非空有界.

注2由h(5)的连续性易知，在条件2下，Z*为非空有界.

条件3由算法1产生的序列{zk=(εk,xk,tk)}满足

∞.

定理2设{zk}是算法1产生的无穷序列.若条件3成立，则{zk}的任意聚点都是Ψ(z)的稳定点.

现在研究由算法1所产生点列{zk}的局部收敛性质.进一步给出如下条件:

条件4对任意实数α>0，Ψ(5)的水平集La:={z∈R1+n+m|Ψ(z)≤a}有界.

易见，若条件4成立，则条件2成立.

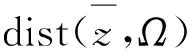
4 数值试验

应用算法1求解如下带“约束”的非线性互补问题.

例1求x*∈X={x∈R4|h(x)≤0}，使得x*≥0，P(x*)≥0,(x*)TP(x*)=0,其中

.

例2求x*∈X={x∈R4|h(x)≤0}，使得x*≥0，P(x*)≥0,(x*)TP(x*)=0,其中

.

例3求x*∈X={x∈R4|h(x)≤0}，使得x*≥0，P(x*)≥0,(x*)TP(x*)=0,其中

.

例4求x*∈X={x∈R5|h(x)≤0}，使得x*≥0，P(x*)≥0,(x*)TP(x*)=0,其中

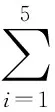
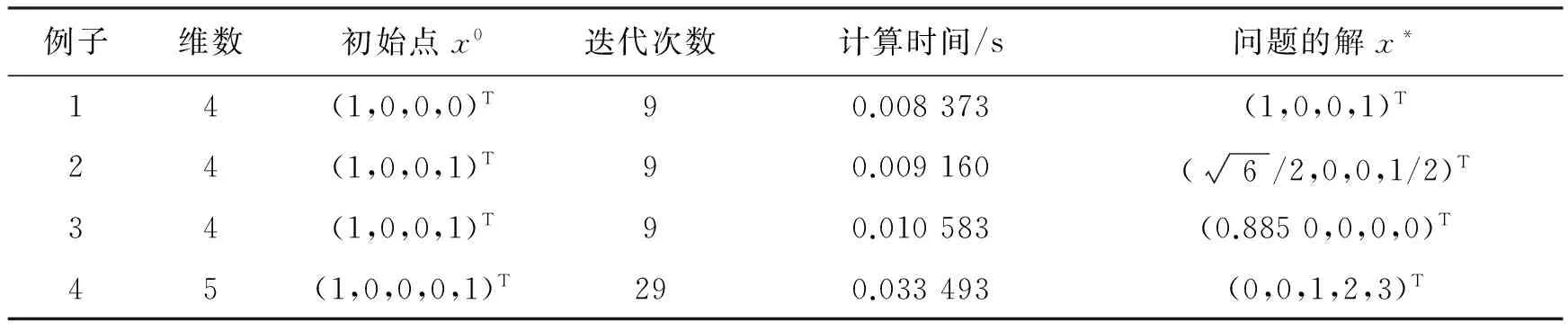
表1 例1～例4的数值试验结果

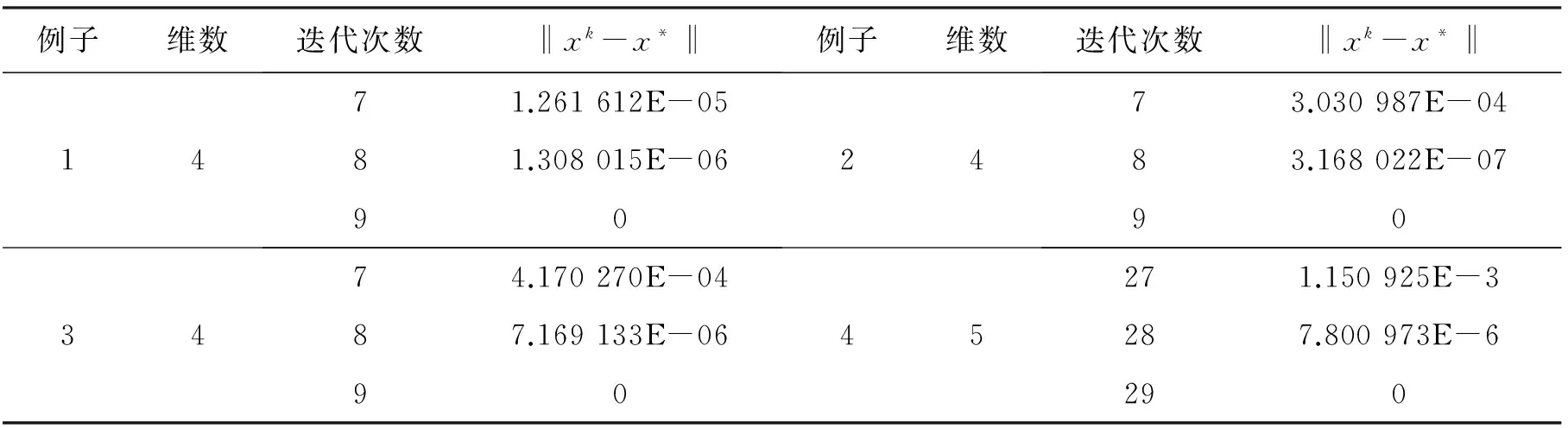
表2 例1～例4最后3步迭代的相关数据

[1]Chen Chunhui,Mangasarian O L.A class of smoothing functions for nonlinear and mixed complementarity problems[J].Computational Optimization and Applications,1996,5(1):97-138.

[2]Facchinei F,Pang J S.Finite-dimensional variational inequalities and complementarity problems I-II[M].New York:Springer-Verlag,2003:1-124.

[3]Ling Chen,Ni Qin,Qi Liqun,et al.A new smoothing Newton-type algorithm for semi-infinite programming[J].Journal of Global Optimization,2010,47(1):133-159.

[4]Yamashita N,Fukushima M.On the rate of convergence of the Levenberg-Marquardt method[J].Computing,2001,15(suppl):239-249.

[5]Dan H,Yamashita N,Fukushima M.Convergence properties of the inexact Levenberg-Marquardt method under local error bound conditions[J].Optimization Methods and Software,2002,17(4):605-626.

[6]Tong X J,Qi L.On the convergence of a trust region method for solving constrained nonlinear equations with degenerate solution[J].Journal of Optimization and Theory Applications,2004,123(1):187-211.

[7]Wang Tao,Monteiro R D C,Pang Jongshi.An interior point potential reduction method for constrained equations[J].Mathematical Programming,1996,74(2):159-195.

[8]Sun Defeng,Womersley R S,Qi Houdou.A feasible semismooth asymptotically Newton method for mixed complementarity problems[J].Mathematical Programming,2002,94(2):167-187.

[9]Clarke F H.Optimization and nonsmooth analysis[M].New York:John Wiley and Sons,1983:69-75.

(责任编辑 陶立方)

ALevenberg-Marquardtalgorithmforsolvingnonsmoothequations

ZHENG Ling′ai， LING Chen

(InstituteofOperationalResearchandCybernetics,HangzhouDianziUniversity,HangzhouZhejiang310018,China)

A new smoothing Levenberg-Marquardt algorithm was presented for solving nonsmooth constrained system of equations, which only needed to solve one strictly convex quadratic programming at each iteration. First, the original problem was converted into an unconstrained system of equations by using the absolute value function of the slack variables, then a Levenberg-Marquardt algorithm was designed by combining the smoothing technique. The presented algorithm converged globally, and converged locally quadratically under an error bound assumption which was much weaker than the standard nonsingularity condition. Some numerical results for the presented method indicated that the algorithm performed quite well in practice.

constrained equations; smoothing technique; Levenberg-Marquardt algorithm; strong semi-smoothness; convergence

O241;O221

A

1001-5051(2013)04-0417-05

2013-06-16

国家自然科学基金资助项目(10871168;11171083)；浙江省自然科学基金资助项目(Y6100366)

郑玲爱(1989-)，女，浙江衢州人，硕士研究生.研究方向：非线性规划.