一维费米原子系统中的拓扑超流和Majorana费米子*

高先龙, 陈 捷， 陈阿海

(浙江师范大学 数理与信息工程学院,浙江 金华 321004)

一维费米原子系统中的拓扑超流和Majorana费米子*

高先龙, 陈 捷， 陈阿海

(浙江师范大学 数理与信息工程学院,浙江 金华 321004)

通过数值求解Bogoliubov de Gennes方程，研究了具有自旋轨道耦合作用的一维费米晶格系统的性质.结果表明:在有限的自旋轨道耦合下和一定的磁场强度时，系统具有零能,此时的准粒子即为Majorana费米子.准无序效应研究表明，Majorana费米子不会被弱准无序所破坏.

拓扑超流；光晶格；Majorana费米子;零能；准无序

0 引 言

自1995年超冷原子的玻色-爱因斯坦凝聚(BEC)实现以来,原子冷却、捕获和操纵的技术得到进一步的发展.目前,实验人员利用光学晶格可以很“干净”地模拟和仿真出凝聚态物理系统中的许多模型,例如强关联体系的Hubbard模型[1]和无序体系中的Anderson模型等[2].如今,在冷原子实验中可以实现单原子分辨技术,可以对几乎全部实验参数进行大范围调节,可以人造规范场,实现有效磁场[3]、自旋-轨道耦合等等[4].这些技术的发展也给理论工作者提出了更多的机遇和更大的挑战,由此引发了更深更广的探索.本文的主要目的就是利用冷原子实验中实现的自旋轨道耦合效应,讨论可能出现的拓扑超流和Majorana费米子,以及其中的无序效应.在论述主要研究内容之前,先介绍一下拓扑超流、Majorana费米子、p-波超导及其研究背景.

随着2005-2006年量子自旋霍尔效应的理论预言[5]及随后的实验观察[6],一类能够实现量子自旋霍尔效应的量子拓扑态——拓扑绝缘体开始受到广泛关注,并在理论与实验两方面都取得了重要突破.拓扑绝缘体从本质上区别于任何已知的物态,是一种新的量子物态,拥有重要的科学意义.它的体元激发由于能隙的存在而没有载流子运动,属于绝缘体,但在系统的边缘处具有受拓扑保护的无能隙边缘激发,导致载流子得以在样品的边界处传导.无能隙边缘激发是具有非阿贝尔统计的任意子(anyons),类似于填充υ=5/2分数量子霍尔效应的Pfaffian态.后者的产生需要外加磁场,破坏了时间反演对称性,而拓扑绝缘体中的表面电子结构源于体材料中非常强的自旋轨道耦合效应,受到时间反演对称性的保护,是一种拓扑序态.因而,它的表面态与表面的具体结构无关,完全是由材料的体电子态的拓扑结构所决定.拓扑态的分类可由拓扑量子数决定[7],其方式不同于Landau对称破缺的范式.

具有非零拓扑数的边界态的存在对有限体系来说是非常重要的[8].当向拓扑序态引入某种对称性破缺时,就有可能激发出新奇量子现象,并导致与之相关的量子器件的问世[9].2008年,Fu等[10]论证了拓扑绝缘体和普通的s-波超导体的结合体,利用邻近效应(proximity effect)产生s-波超导配对电子,其界面电子的性质类似于p-波超导体,因此也可以有Majorana 费米子:一种反粒子就是它本身的粒子(由意大利物理学家Ettore Majorana于1937年提出).在此类体系中产生Majorana 费米子的关键是拓扑绝缘体表面态的强自旋轨道耦合作用,以及表面态处Kramer简并的破坏.也可进一步把拓扑绝缘体和磁性薄膜结合,如最近的实验,在超导材料——NbSe2单晶表面,以分子束外延法生长出拓扑绝缘体薄膜——Bi2Se3,从而形成了Bi2Se3/NbSe2复合材料体系.此体系具有超导态与拓扑序态共存的特点,为探寻Majorana费米子和进一步调控拓扑绝缘体的拓扑电子态找到了重要的突破口[11-12].2000年,Read等[13]指出二维体系中无自旋的费米子通过p-波超导耦合的低能激发(所谓Bogoliubov准粒子)是Majorana费米子.Kitaev[12]进一步论证了一维p-波超导体的两端也会出现Majorana费米子,但是在如今的实验材料中,稳定的p-波超导体很难找到.2010年,Sau的研究团队[14]意识到半导体二维电子气中也有强自旋轨道耦合,所以他们进一步简化Fu等的模型,不用拓扑绝缘体,代之以更常见的半导体材料,并通过磁场破坏时间反演对称性,从而也得到类似于p-波超导体的Majorana费米子模型.结合Kitaev的工作,一个自然的想法就是用半导体量子线加上超导体来实现一维的p-波超导体,而其边界就会出现要寻找的Majorana费米子.很快在实验中[15]把一根半导体量子线放在一块s-波超导体上,通过邻近效应在量子线中诱导出s-波配对,然后加上一个平行于量子线的塞曼磁场来破坏时间反演.实验上能够调节的参数是磁场的强度和半导体线中的费米能.当这2个参数满足一定的条件时,量子线的两端就会出现零能量的Majorana费米子.

目前实现Majorana费米子的方案有:1)一维p-波超导体;2)二维px+ipy体系;3)拓扑绝缘体和超导体组成的异质结;4)自旋轨道耦合的半导体和超导体组成的异质结.那么，还可以在哪些材料或系统中找到Majorana费米子呢?近来，随着人造规范场的诞生,人们开始对冷原子体系中的自旋轨道耦合产生了兴趣[4].在冷原子体系中,利用拉曼光实现人造规范场,随时间变化的人造规范场可以模拟电场,随空间变化的人造规范场可以模拟磁场[3].有学者利用人造规范场在玻色系统中通过非Abelian人造规范场产生了自旋轨道耦合效应[3].文献[16]用40K和文献[17]用6Li在费米体系中也实现了等权的Rashba-Dresselhaus自旋轨道耦合效应.这样人们不仅可以在冷原子体系中量子模拟具有自旋轨道耦合的固态系统,还可以在冷原子实验中实现和操纵更多固态体系中不存在的结构和物理性质[18].

由上所述,不用固体系统中的纳米线结构,也可以用一维具有自旋轨道耦合的费米原子气,加上诱导出的s-波超流和改变不同精细结构粒子数目引入的有效磁场就可以实现对一维拓扑超流和Majorana配对的模拟.早期有用二维冷原子产生Majorana费米子的方案[19]。近期,文献[20]提出利用光捕获的一维费米原子气来产生:通过光子反冲的光学拉曼跃迁耦合原子的2个态,并诱导出有效自旋轨道耦合和有效磁场,再加上三维分子BEC背景诱导的s-波配对,从而得到一个类似于半导体量子线的模型;而Majorana费米子的检测可用空间分辨的射频谱(radio-frequency spectroscopy)测量局域态密度,类似于凝聚态体系中的扫描隧道显微镜技术.最近，理论物理学家设计用二维具有自旋轨道耦合和超流的费米系统实现Majorana费米子[21-22],讨论了准一维体系带来的新的物理[23];利用二维体系中拓扑超流相中的涡旋激发产生Majorana零模[24-28],用一维具有d-波超流的自旋轨道耦合系统操纵Majorana费米子[29],另外也讨论了相互作用对一维费米体系中拓扑相的影响[30].目前，对于拓扑性和无序关系等方面及拓扑表面态的弱局域化和反局域化的研究也已开展[31-32].通过讨论一维p-波超导下准无序强度驱动的拓扑超流和Majorana配对[31],发现了通过调节相移及密度调制的p-波超导线可出现零模的Majorana边界态.研究表明:拓扑超流的边界态由于其非局域的拓扑性不受局域弱无序所干扰,强局域无序可导致拓扑非平凡的绝缘行为,称为拓扑Anderson绝缘体[33],冷原子中产生的speckle无序具有空间关联性,为长程无序,长程无序的体系具有不同的拓扑Anderson绝缘体性质[34〗[35],是个重要的课题.

相比于凝聚态体系,冷原子系统具有一些优势,如:可产生长量子线,从而实现空间上分离的具有长距离量子关联的Majorana费米子对,这样就保证量子计算中的比特数据不受外界的干扰;对三维空间的1个或2个维度进行强束缚可以实现二维或一维系统;相互作用可调;杂质可控:单杂质,准无序,以及speckle无序等在实验上的实现都很成熟.本文通过对具有自旋轨道耦合的一维晶格系统进行数值研究,结果表明:在磁场强度满足一定条件时,系统可以出现Majorana费米子,此Majorana费米子对无序具有较强的免疫力.

1 理论模型

笔者将主要考虑受限的具有自旋轨道耦合作用的费米气,如进一步在y-z平面方向加上强二维光晶格,就会形成很多沿x方向的一维束丛,在其中的一束,原子运动可看成一维的,此方向运动的原子可以用谐振势、量子环或hard-wall来束缚.如在此方向再加光晶格则可形成一维的晶格系统.自旋轨道耦合可由一对耦合2个自旋态且方向相反的拉曼光来产生,拉曼光沿x方向.以连续体系为例,这样的准一维体系可由单通道的模型哈密顿量

来描述.式(1)中:

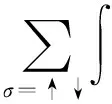
Hint=gdxΨ+↑(x)Ψ+↓(x)Ψ↓(x)Ψ↑(x).

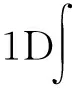
(3)

式(1)和式(2)中：σ=↑,↓表示2个超精细态;Ψσ(x)为x方向质量为m、自旋为σ的费米场消灭算符;ΩR是拉比频率，描述两光子拉曼光的耦合强度;kR=(2π)/λR由2束激光的波长λR确定,因此,2ћkR为散射中的动量转移;μ(x)用于描述相应的化学势,杂质或无序(可为x的函数);Vtrap(x)=(mω2x2)/2描述轴向的谐振束缚势.为了进一步明确两光子拉曼散射带来的自旋轨道耦合,引入局域规范变换以消除拉曼耦合项中的空间依赖性,

这样原哈密顿量则变为

哈密顿量(5)变为

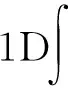
若在x方向加一足够深的光晶格,并用Wannier函数展开,则可得到相应具有自旋轨道耦合的晶格体系的模型哈密顿量,

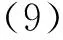
具体每一项为

式(10)中的4项分别描述格点间的动能跃迁同格点的相互作用,自旋轨道耦合和Zeeman场、强度分别为t,U,αR,h.这里的μi可用于描述化学势、杂质、无序或束缚势.

对于光晶格中的杂质问题,在实验中有很多办法可以操控,如用去共振的涡旋激光场或另一种原子或离子来产生单个杂质,利用激光照射到扩散板上产生随机分布的speckle无序或通过另一对激光产生准无序.一维体系由在横向的y-z方向上加很强的二维光晶格来产生,此时可在x方向加额外的谐振束缚原子,或加一光晶格,从而分别实现连续空间和离散空间的准一维Fermi体系.自旋轨道耦合可用前面提到的非Abelian人造规范场技术来产生.所以,在目前的冷原子实验中实现Hcom0,Hdis0这2种体系是可行的.

本文主要研究光晶格体系所描述的具有自旋轨道耦合的低维混合费米冷原子气系统,探讨其中的拓扑超流性,Majorana费米子的形成和操纵,准无序对体系量子相的影响,特别是拓扑相的影响.

2 数值结果及讨论

首先研究方程(10)在配对超流的近似下,

系统的能谱特征,其中Δi描述了格点i处吸引相互作用诱导的s-波配对强度.引入Bogoliubov de Gennes (BdG)变换,可得到BdG方程:

式(12)中,

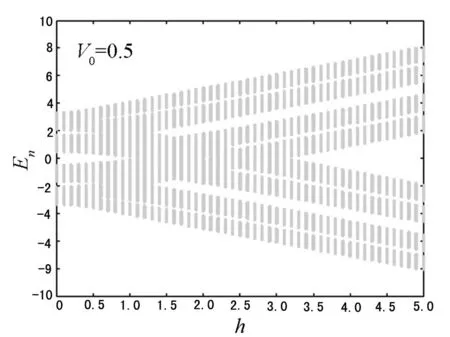
图1是均匀配对强度下系统的能谱随磁场的变化图,系统具有hard-wall,其他的参数为Δ=0.5,μ=-1,αR=1,L=100(在计算中取能量单位t=1,晶格常数a=1).从图1中可以看出,系统的能谱具有粒子-空穴对称性.在有限的s-波配对能隙假设下,能量中正的部分在hc1=1.2处下降到零,并在hc2=3处再次上升,即系统在hc1≤h≤hc2处出现零能,零能的出现意味着系统中的准粒子可能是Majorana费米子,笔者将画出其波函数,并数值证明其即为Majorana费米子.

在这个系统中,可能的Majorana费米子的出现需要2个条件:存在自旋轨道耦合和磁场,自旋轨道耦合消除Kramer简并,而磁场则破坏了时间反演对称性.其中自旋轨道耦合强度的大小对Majorana费米子的出现并没有太大的影响,如图2所示,αR=1,2,3,5对应着相同的临界磁场强度.

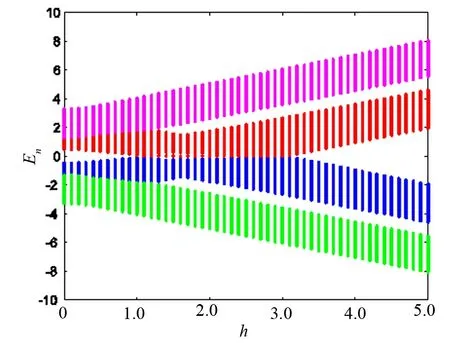
图1 均匀配对强度下系统的能谱随磁场的变化图 图2 能隙和磁场的变化关系

为了验证零能对应着Majorana费米子的出现,笔者引入Majorana算符,

满足γA+iσ=γAiσ,γB+iσ=γBiσ.以此可得到相应Majorana费米子的波函数,其与BdG方程本征态的关系为

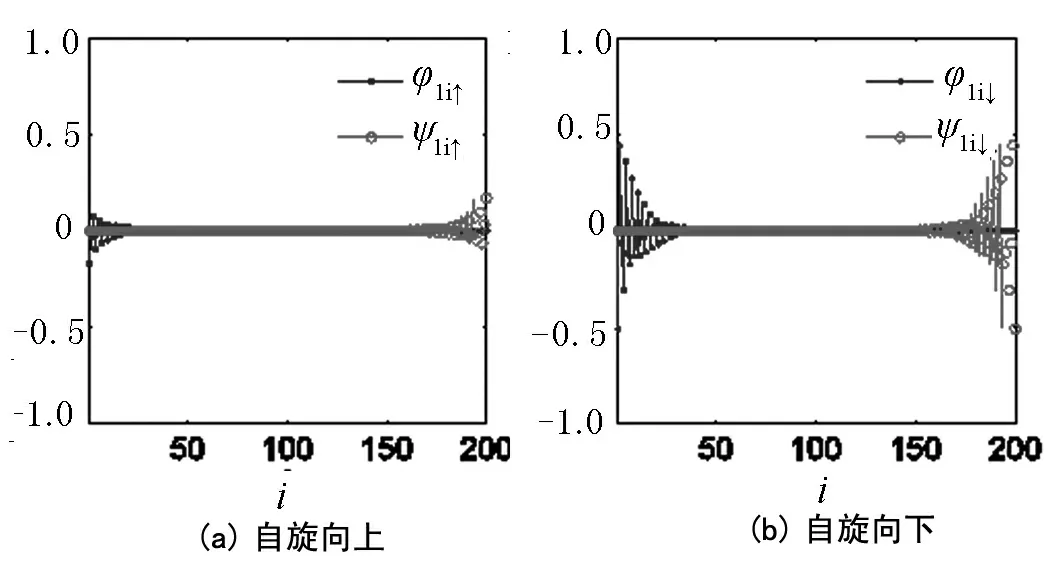
图3给出了最低能态n=1对应的自旋向上(图3(a))和向下(图3(b))的一对Majorana费米子的波函数,可以看出它们分别局域在系统的左边界和右边界处.

Majorana费米子对无序有很强的抵抗力.这里讨论冷原子实验中可以实现的准无序效应,

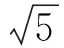
3 结 论

本文系统介绍了量子自旋霍尔效应、Majorana费米子、拓扑绝缘体、p-波超导体和s-波超流的Majorana费米子等概念以及自旋轨道耦合作用对拓扑量子计算的重要意义.

通过对具有自旋轨道耦合的一维s-波超流费米体系的研究,表明体系在2个临界的磁场范围内存在零能区,其对应的准粒子是Majorana费米子,自旋轨道耦合的强度对出现Majorana费米子的参数范围影响较小,Majorana费米子对准无序具有很强的免疫力.所以,具有自旋轨道耦合的冷原子系统可以用来验证Majorana费米子的存在,从而提供一个进行量子计算的可操作体系.

今后的研究将涉及到态密度分布、无序参与度等的计算并以此确定准无序的V0-h相图.其他有意义的研究还包括:不同无序如长程无序和磁杂质或无序对相图的影响;一维体系中的边界迁移率问题;相互作用对Majorana费米子的影响等等.

[1]Lewenstein M,Sanpera A,Ahufinger V,et al.Ultracold atomic gases in optical lattices:mimicking condensed matter physics and beyond[J].Adv Phys,2007,56:243-379.

[2]Billy J,Josse V,Zuo Zhanchun,et al.Direct observation of Anderson localization of matter waves in a controlled disorder[J].Nature,2008,453:891-894.

[3]Lin Y J,Compton R L,Jiménez-García K,et al.Synthetic magnetic fields for ultracold neutral atoms[J].Nature,2009,462:628-632.

[4]Lin Y J,Jimenez-Garcia K,Spielman I B.Spin-orbit-coupled Bose-Einstein condensates[J].Nature,2011,471:83-86.

[5]Kane C L,Mele E J.Z2topological order and the quantum spin hall effect[J].Phys Rev Lett,2005,95:146802.

[6]König M,Wiedmann S,Brüne C,et al.Quantum spin hall insulator state in HgTe quantum wells[J].Science,2007,318:766-770.

[7]Wen X G.Quantum field theory of many-body systems[M].New York:Oxford University,2004.

[8]Halperin B I.Quantized hall conductance,current-carrying edge states,and the existence of extended states in a two-dimensional disordered potential[J].Phys Rev B,1982,25:2185-2190.

[9]Winkler R.Spin-orbit coupling effects in two-dimensional electron and hole systems[M].Berlin:Springer-Verlag,2003.

[10]Fu L,Kane C L.Superconducting proximity effect and majorana fermions at the surface of a topological insulator[J].Phys Rev Lett,2008,100:096407.

[11]Wang Meixiao,Liu Canhua,Xu Jinpeng,et al.The coexistence of superconductivity and topological order in the Bi2Se3Thin films[J].Science,2012,336:52-55.

[12]Kitaev A Y.Unpaired majorana fermions in quantum wires[J].Physics-Uspekhi,2001,44:131-136.

[13]Read N,Green D.Paired states of fermions in two dimensions with breaking of parity and time-reversal symmetries and the fractional quantum Hall effect[J].Phys Rev B,2000,61:10267-10297.

[14]Lutchyn R M,Sau J D,Das Sarma S.Majorana fermions and a topological phase transition in semiconductor-superconductor heterostructures[J].Phys Rev Lett,2010,105:077001.

[15]Mourik V,Zuo K,Frolov S M,et al.Signatures of majorana fermions in hybrid superconductor-semiconductor nanowire devices[J].Science,2012,336:1003-1007.

[16]Wang Pengjun,Yu Zengqiang,Fu Zhengkun,et al.Spin-orbit coupled degenerate fermi gases[J].Phys Rev Lett,2012,109:095301.

[17]Cheuk L W,Sommer A T,Hadzibabic Z,et al.Spin-injection spectroscopy of a spin-orbit coupled Fermi gas[J].Phys Rev Lett,2012,109:095302.

[18]Dalibard J,Gerbier F,Juzseliunas G,et al.Artificial gauge potentials for neutral atoms[J].Rev Mod Phys,2011,83:1523-1543.

[19]Zhang Chuanwei,Tewari S,Lutchyn R M,et al.Px+ipysuperfluid froms-wave interactions of Fermionic cold atoms[J].Phys Rev Lett,2008,101:160401.

[20]Jiang L,Kitagawa T,Alicea J,et al.Majorana Fermions in equilibrium and in driven cold-atom quantum wires[J].Phys Rev Lett,2011,106:220402.

[21]Liu Xiaji,Hu Hui.Topological superfluid in one-dimensional spin-orbit-coupled atomic Fermi gases[J].Phys Rev A,2012,85:033622.

[22]Wei R,Mueller E J.Majorana fermions in one-dimensional spin-orbit-coupled Fermi gases[J].Phys Rev A,2012,86:063604.

[23]Zhang R,Wu F,Tang J R,et al.Significance of dressed molecules in a quasi-two-dimensional polarized Fermi gas[J/OL].[2011-08-11].http://arxiv.org/abs/1209.5935.

[24]Zhou Jing,Zhang Wei,Yi Wei.Topological superfluid in a trapped two-dimensional polarized Fermi gas with spin-orbit coupling[J].Phys Rev A,2011,84:063603.

[25]Han W,Zhang S,Liu W M.Spin-orbit coupled Bose-Einstein condensates in spin-dependent optical lattices[J/OL].[2012-11-09].http://arxiv.org/abs/1211.2097.

[26]Zhang Chunwei,Tewari S,Lutchyn R M,et al.Px+ipysuperfluid froms-wave interactions of Fermionic cold atoms[J].Phys Rev Lett,2008,101:160401.

[27]Zhu Shiliang L,Shao L B,Wang Z D,et al.Probing non-abelian statistics of majorana Fermions in ultracold atomic superfluid[J].Phys Rev Lett,2011,106:100404.

[28]Gong Ming,Chen Gang,Jia Suotang,et al.Searching for majorana Fermions in 2D spin-orbit coupled Fermi superfluids at finite temperature [J].Phys Rev Lett,2012,109:105302.

[29]Yan Zhoubo,Yang Xiaosen,Wan Shaolong.Topological superfluid in one-dimensional ultracold atomic system with spin-orbit coupling[EB/OL].[2011-11-08].http://arxiv.org/abs/1111.1952.

[30]Guo Huai,Shen Shunqing.Topological phase in a one-dimensional interacting fermion system[J].Phys Rev B,2011,84:195107.

[31]Lang Lijun,Chen Shu.Majorana fermions in density-modulatedp-wave superconducting wires[J].Phys Rev B,2012,86:205135.

[32]Lu Haizhou,Shi Junren,Shen Shunqing.Competition between weak localization and antilocalization in topological surface states[J].Phys Rev Lett,2011,107:076801.

[33]Groth C W,Wimmer M,Akhmerov A R,et al.Theory of the topological anderson insulator[J].Phys Rev Lett,2009,103:196805.

[34]Girschik A,Libisch F,Rotter S.Topological insulator in the presence of spatially correlated disorder[J].Phys Rev B,2013,88:012401.

[35]Gangadharaiah S,Braunecker B,Simon P,et al.Majorana edge states in interacting one-dimensional systems[J].Phys Rev Lett,2011,107:036801.

(责任编辑 杜利民)

TopologicalsuperfluidandMajoranafermionsinone-dimensionalfermionicatomicsystems

GAO Xianlong， CHEN Jie, CHEN Ahai

(CollegeofMathematics，PhysicsandInformationEngineering,ZhejiangNormalUniversity,JinhuaZhejiang321004,China)

It was studied the properties of one-dimensional fermionic atomic systems of spin-orbital couplings by means of numerically solving the Bogoliubov de Gennes equations. It was showed that, under the finite spin-orbital coupling strength and strong enough magnetic field, the system would be of zero energy, which behaved as the Majorana fermions. The effects of the quasi-disorder on the Majorana wave functions were also studied, which had little influence on the localization of the Majorana fermions.

topological superfluid; optical lattice; Majorana fermions; zero energy; quasi-disorder

O562.4

A

1001-5051(2013)04-0372-07

2013-06-03

国家自然科学基金资助项目(11174253)

高先龙(1973-),男,安徽肥西人,教授,博士.研究方向:低维强关联体系.