不可微非线性方程的非精确牛顿型法的半局部收敛性*

郭晓梅, 徐秀斌, 詹铜霞

(浙江师范大学 数理与信息工程学院,浙江 金华 321004)

不可微非线性方程的非精确牛顿型法的半局部收敛性*

郭晓梅, 徐秀斌, 詹铜霞

(浙江师范大学 数理与信息工程学院,浙江 金华 321004)

在求解非线性算子方程H(x)=0时,若H(x)的导数不存在,则可用非精确牛顿型法代替牛顿法求解;在 Hölder条件及Hölder中心条件下,给出了收敛性判断的条件,及半局部收敛性的证明;最后,给出了一个具体例子进行应用.

不可微非线性算子方程;非精确牛顿型法;半局部收敛;Hölder条件;Hölder中心条件

0 引 言

令X和Y是Banach空间,D是X的一个开凸子集,考虑如下的非线性方程:

求解非线性方程(1)的近似解是一个重要的问题,因为大量的不同类型的实际问题都可归结为对非线性方程的求解,例如微分方程、边界值问题、积分方程等.目前,在H是Fréchet可导的条件下,常常用非精确迭代程序来求解非线性方程(1),其迭代式为(初始点x0给定)

式(2)中,残余序列{rn}的选择影响着非精确牛顿法的收敛性.例如,文献[1-2]给出了非精确牛顿法(2)的半局部收敛定理,其中残余序列{rn}满足

‖rn‖≤ηn‖H(xn)‖,

此时,0≤ηn<η<1.文献[3]利用Lipschitz条件在开集B(x0,δ)里给出了非精确牛顿法(2)的半局部收敛定理,此时{rn}满足

‖H′(x0)-1rn‖≤ηn‖H′(x0)-1H(xn)‖1+β,β≥0.

文献[4]给出了非精确牛顿法(2)的半局部收敛定理,其残余序列{rn}满足

‖H′(x0)-1(rn-rn-1)‖≤ηn‖xn-xn-1‖.

然而,当H不可导时,非精确牛顿迭代法就不能用来求解非线性方程.诸多文献[5-7]考虑将H分解为可导部分F和不可导部分G,即

H(x)=F(x)+G(x).

其中:F:D⊂X→Y是一个Fréchet可导的算子;G:D→Y是一个连续算子.

在这种情况下,也已有诸多研究.例如,文献[5]考虑修正牛顿法

xn+1=xn-(F′(xn))-1(F(xn)+G(xn)),x0∈D,n≥0.

文献[6]考虑迭代

式(3)中,A(xn)∈L(X,Y)是从X到Y的有界线性算子,近似于F(xn)的Fréchet导数F′(xn).文献[7]将非精确牛顿法与式(3)相结合,得到了一种非精确牛顿型迭代法,其表达式为

本文主要通过利用Hölder条件、Hölder中心条件和控制条件‖F′(x0)-1(rn-rn-1)‖≤ηn‖xn-xn-1‖,研究非精确牛顿型迭代法(4)的半局部收敛性,其中0≤ηn<η<1.

1 半局部收敛性分析

首先给出引理,然后在引理的基础上证明非精确牛顿型迭代法(4)的半局部收敛性.

引理1假设存在常数L≥0,ω1≥0,L0≥0,μ1≥0,η≥0,β≥0,p∈(0,1],q∈(0,1),使得

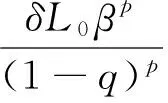
式(5)中:α=(p+1)(ω1+μ1+η);δ=q(p+1).则由t0=0,t1=β,

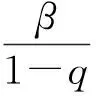
证明 先用归纳法证明式(7)和如下2个式子同时成立:

当n=0时,由t0=0,t1=β有

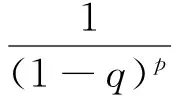
因为Lβp+δL0βp+α<δ(1-ω1)成立,所以

δ(1-ω1)-δL0βp>Lβp+α;

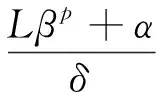
因此,

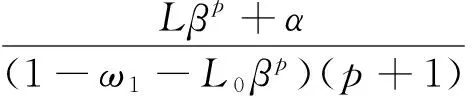
则当n=0时,式(7)～式(9)成立.

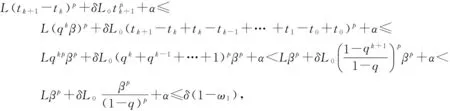
(12)

从而可得对于n=k时式(8)成立.

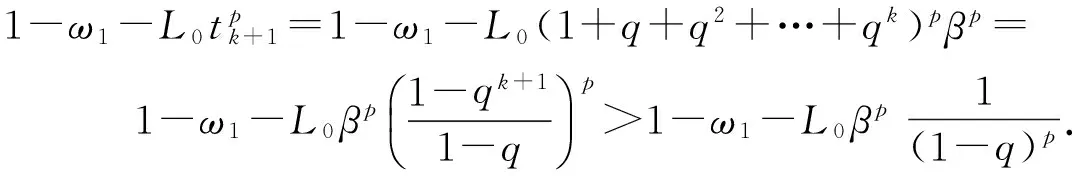
(13)

因为

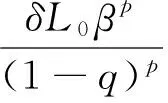
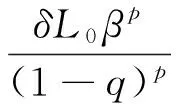
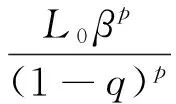
将上面3个式子代入式(13),可得1-ω1-L0tpk+1>0,即式(9)成立.

因为δ=q(p+1),所以

L(tk+1-tk)p+δL0tpk+1+α≤δ(1-ω1);

L(tk+1-tk)p+α≤δ(1-ω1-L0tpk+1);

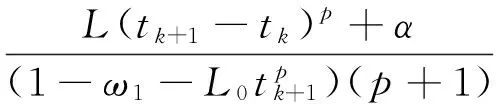
当n=k时,

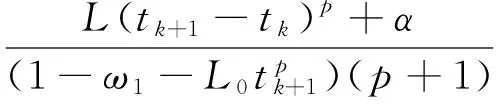
又由式(14)可得tk+2-tk+1≥0,即当n=k时式(7)成立.因此,当n=k时,式(7)～式(9)成立.

最后证tn≤t**.由于

所以,当n=0,1,2时,tn≤t**成立.假设对于所有n≤k-1,tn≤t**均成立,则当n=k时

tk≤tk-1+q(tk-1-tk-2)≤tk-2+q(tk-2-tk-3)+q(tk-1-tk-2)≤…≤

t1+q(t1-t0)+q(t2-t1)+…+q(tk-1-tk-2)≤

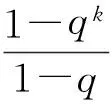
(15)

所以{tn}单调递增有界,收敛于t*≤t**且有

0≤tn+2-tn+1≤q(tn+1-tn)≤…≤qn+1t1=qn+1β.

引理1证毕.

根据引理1,给出非精确牛顿型迭代法(4)的半局部收敛定理.

定理1假设F:D⊂X→Y是一阶连续Fréchet可导的非线性算子,G:D→Y是一连续算子,D是X的开凸子集,A(x)∈L(X,Y)近似于F′(x).若存在初始点x0∈D,使得F′(x0)-1∈L(Y,X)及A(x0)-1∈L(Y,X)存在,且有常数p∈(0,1],β≥0,μ1≥0,L≥0,L0≥0,ω1≥0,0≤ηn<η<1(n=0,1,2,…),对于所有的x,y∈D,有

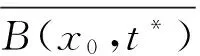
其中,{tn}如引理1所定义.若存在R0≤t*,使得

证明 先证

当k=0时,由式(4)有

‖x1-x0‖=‖A(x0)-1(F(x0)+G(x0)-r0)‖≤β=t1-t0.

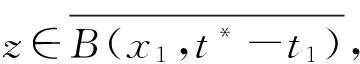
‖z-x0‖≤‖z-x1‖+‖x1-x0‖≤t*-t1+t1-t0=t*-t0,

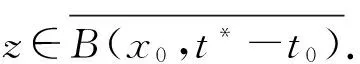
下面假设当k=n-1时结论成立,即有

当k=n时,

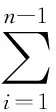
对θ∈(0,1), 有

‖xn-1+θ(xn-xn-1)-x0‖≤‖xn-1-x0‖+θ‖xn-xn-1‖≤tn-1+θ(tn-tn-1)≤t*.

由式(9)、式(19)和式(20)可得

‖F′(x0)-1(A(xn)-F′(x0))‖=‖F′(x0)-1(A(xn)-F′(xn)+F′(xn)-F′(x0))‖≤

‖F′(x0)-1(A(xn)-F′(xn))‖+‖F′(x0)-1(F′(xn)-F′(x0))‖≤ω1+L0tpn<1.

故由Banach引理有

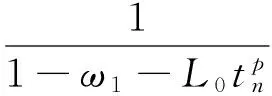
由式(17)、式(18)、式(20)及式(21)可推得

‖F′(x0)-1(F(xn)+G(xn)-rn)‖≤

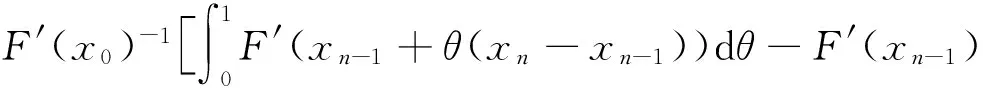
‖F′(x0)-1(F′(xn-1)-A(xn-1))‖5‖xn-xn-1‖+

(28)

所以,由式(27)、式(28)及引理1可得

‖xn+1-xn‖=‖A(xn)-1(F(xn)+G(xn)-rn)‖≤

‖A(xn)-1F′(x0)‖5‖F′(x0)-1(F(xn)+G(xn)-rn)‖≤

(29)

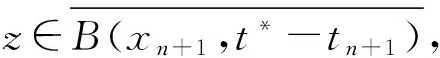
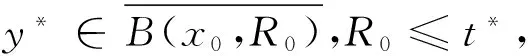
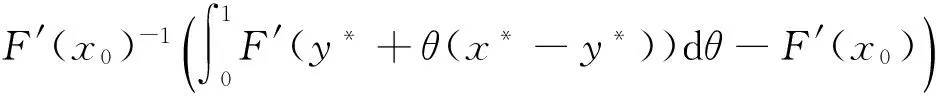
L0∫10[θt*+(1-θ)R0]pdθ<1.

2 应 用

下面考虑一个特殊的非线性算子,即第二类Hammerstein积分方程.

令μ∈R,p∈(0,1],

式(30)中:l(s)是一个连续函数,对∀s∈[a,b],l(s)>0;g是[a,b]×[a,b]上的非负连续函数.若g(s,t)是定义如下的格林函数:

则式(30)等价于如下的边界值问题:

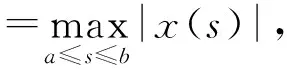
则式(30)相当于[H(x)](s)=0的解.令

则有

令x0∈C[a,b],则

‖I-F′(x0)‖≤M((1+p)‖x0‖p+μ).

则

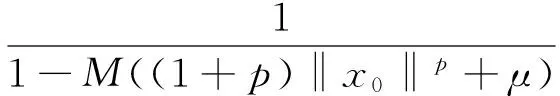
又因为

所以

‖F′(x)-F′(y)‖≤M(1+p)‖x-y‖p,

因此,

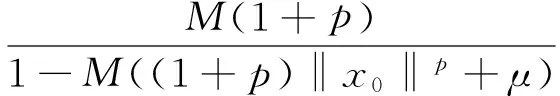
文献[3,7-8]都对此问题有应用研究.本文考虑一个特殊的第二类Hammerstein积分方程,用以说明定理1的优越性.

令a=0,b=1,

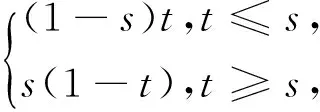
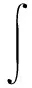
则

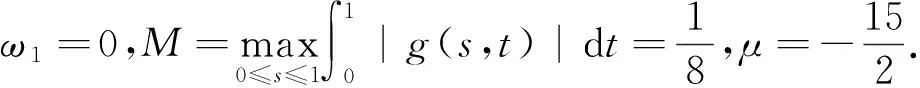
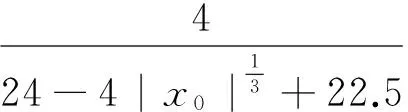
又根据‖F′(x0)-1(G(x)-G(y))‖≤μ1‖x-y‖得

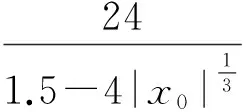
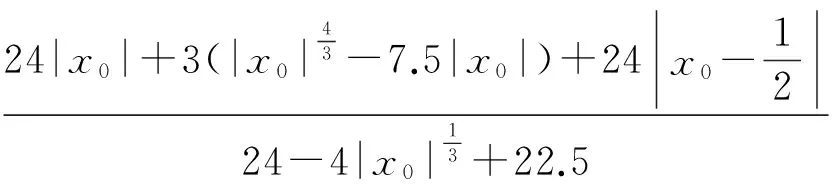
取x0=0,η=maxηn=0.1,q=0.8,则

|M((1+p)‖x0‖p+μ)|=0.937 5<1.

即式(31)成立.将L,L0,β,α,p,δ的值代入引理1,可得式(5)成立,即

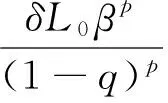
由定理1的证明过程知,可以用非精确牛顿型法(4)解决此问题.

[1]Dembo R S,Eisenstat S C,Steihaug T.Inexact Newton methods[J].Numer Anal,1982,19(2):400-408.

[2]Eisenstat S C,Walker H F.Choosing the forcing terms in an inexact Newton method[J].SIAM J Sci Comput,1996,17(1):16-32.

[3]Argyros I K,Ren H.Kantorovich-type semilocal convergence analysis for inexact Newton methods[J].Comput Appl Math,2011,235(9):2993-3005.

[4]Guo Xueping.On semilocal convergence of inexact Newton methods[J].Comput Math,2007,25(2):231-242.

[5]Argyros I K.The Newton-Kantorovich method under mild differentiablility conditions and the Ptk error estimates[J].Mh Math,1990,109(3):175-193.

[6]Argyros I K.A convergence theorem for Newton-like methods under generalized Chen Yamamoto-type assumptions[J].Appl Math Comput,1994,61(1):25-37.

[7]Argyros I K,Hilout S.Weak convergence conditions for inexact Newton-type methods[J].Appl Math Comput,2011,218(6):1-10.

[8]Shen Weiping,Li Chong.Convergence criterion of inexact methods for operators with Hölder continuous derivatives[J].Taiwanese Journal of Math,2008,12(7):1865-1882.

(责任编辑 陶立方)

SemilocalconvergenceofaninexactNewton-typemethodforsolvingnondifferentiableequations

GUO Xiaomei, XU Xiubin, ZHAN Tongxia

(CollegeofMathematics,PhysicsandInformationEngineering,ZhejiangNormalUniversity,JinhuaZhejiang321004,China)

It was focused on solving a kind of nonlinear operator equationsH(x)=0 without differentiability of the operator. An inexact Newton-type method was constructed, the semilocal convergence under the Hölder condition and the Hölder center condition was obtained. Finally, a numerical example was used as an application.

nondifferentiable nonlinear operator equation; inexact Newton-type method; semilocal convergence; Hölder condition; Hölder center condition

O241

A

1001-5051(2013)04-0401-07

2013-05-10

国家自然科学基金资助项目(61170109)

郭晓梅(1989-),女,浙江金华人,硕士研究生.研究方向:非线性数值逼近.