赋p-Amemiya范数的Musielak-Orlicz函数空间的复凸性*

崔云安，牛金玲，陈丽丽

(哈尔滨理工大学)

0 引言

1967 年，Thorp E 与 Whitley R［1］首次引入复端点的概念，1987年，吴从炘、孙慧颖［2-4］讨论了矢值Musielak-Orlicz函数空间的复端点的刻画问题，并给出该空间中复严格凸性和复一致凸性的充要判据.2008年，崔云安等［5］在Orlicz空间中引入了p-Amemiya范数的定义，证明了它与经典的Orlicz范数和Luxemburg范数是等价的，并给出赋p-Amemiya范数的Orlicz空间中端点的刻画.2009年，崔云安，Hudzik H 等［6］继续研究了赋p-Amemiya范数的Orlicz空间的强端点的充要判据问题.

1 预备知识

(X，‖·‖X)表示定义在复数域C上的复Banach空间，B(X)和S(X)分别表示该空间的闭单位球和单位球面.

定义1.1［7］(T，∑，μ)表示非原子完备的测度空间，μ(T)＜∞.Φ是Musielak-Orlicz函数是指 Φ:T×［0，+∞)→［0，+∞］满足:

(1)对μ-a.e.t∈T，Φ(t，u)是μ-可测函数，对任意的u∈［0，+∞);

(3)Φ(t，u)关于 u是［0，∞)上的凸函数.

令 e(t)=sup{u ≥0:Φ(t，u)=0}，

E(t)=sup{u ≥0;Φ(t，u)＜ ∞}则e(t)和E(t)都是μ-可测函数.

定义1.2［7］(X，‖·‖)表示复Banach空间，记XT表示所有从T到X的μ-可测函数的全体，对任意的x∈XT，定义如下模函数:

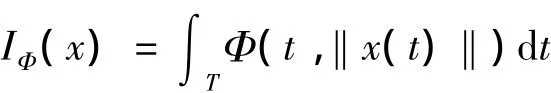
由它生成相应的Musielak-Orlicz函数空间

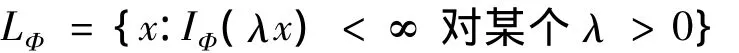
对Musielak-Orlicz函数空间LΦ赋予如下范数p-Amemiya范数

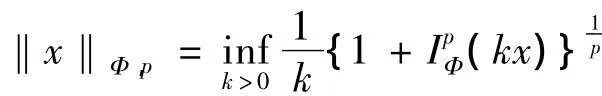
即为一个 Banach 空间，记为 LΦ，p=(LΦ，‖·‖Φ，p).

定义1.3x∈S(X)为B(X)的复端点是指对∀y∈X{0}，有

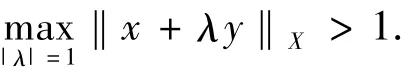
定义1.4［8］设(X，‖·‖X)是复Banach空间，x∈S(X)是B(X)的复强端点是指对任意的 ε ＞ 0，Δc(x，ε)＞ 0，其中

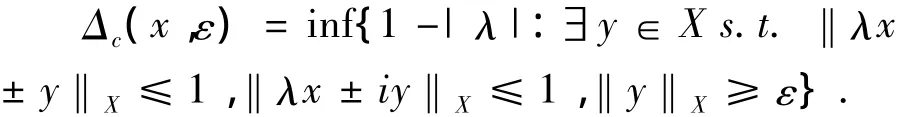
引理1.5［7］对任意的 ε ＞ 0，存在 δ∈使得若 u，v∈ C，且

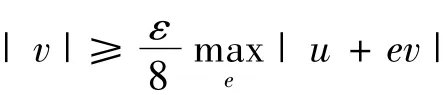
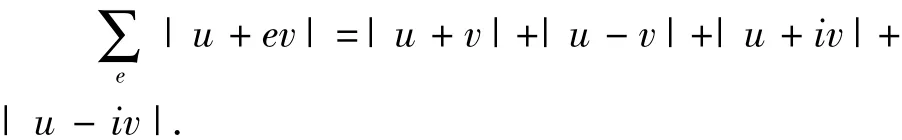
2 主要结果

定理2.1 设1≤ p＜∞，p是奇数，x∈S(LΦ，p)，则如下结论等价:

(i)x是 B(LΦ，p)的复强端点;

(ii)x是 B(LΦ，p)的复端点;

(iii)对∀k∈Kp(x)，有μ{t∈T:k|x(t)|＜e(t)}=0.

证明 (i)⇒(ii)是显然的.

(ii)⇒(iii)设 x∈S(LΦ，p)是 B(LΦ，P)的复端点，且存在∀k0∈Kp(x)使得μ{t∈T:k0|x(t)|＜e(t)}＞0.易知可找到公共的d＞0及T0∈∑满足μ(T0)＞0且使得

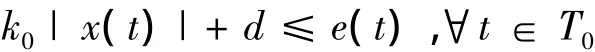
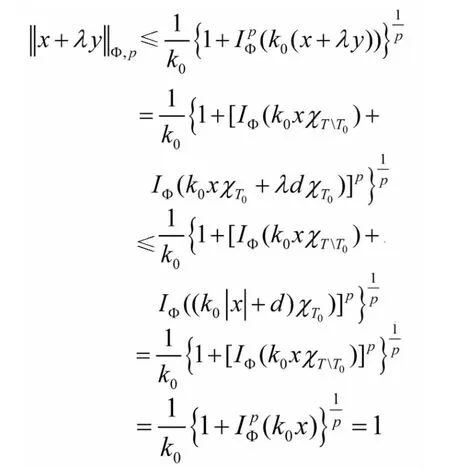
这与假设的x是B(LΦ，p)的复端点矛盾.

(iii)⇒(i)假设 x0不是B(LΦ，p)的复强端点，由定义1.4知存在ε0＞0使得

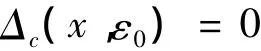
即存在 λn∈ C，| λn|→ 1，yn∈ LΦ，p，满足‖yn‖Φ，p≥ ε0使得

‖λnx0± yn‖Φ，p≤1，‖λnx0± iyn‖Φ，p≤1由此可知

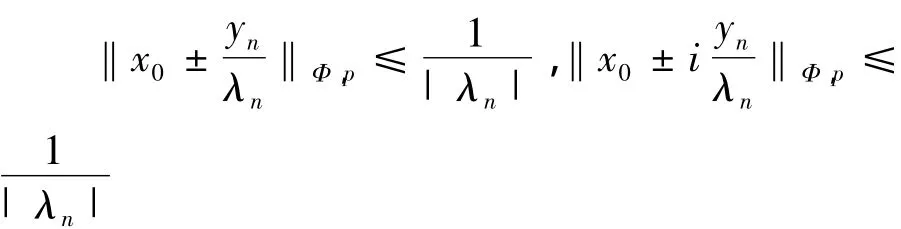
对上述的ε0＞0，由引理1.5知，存在，使得若 u，v∈ C，

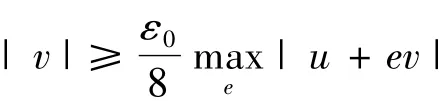
对每个n∈N，令

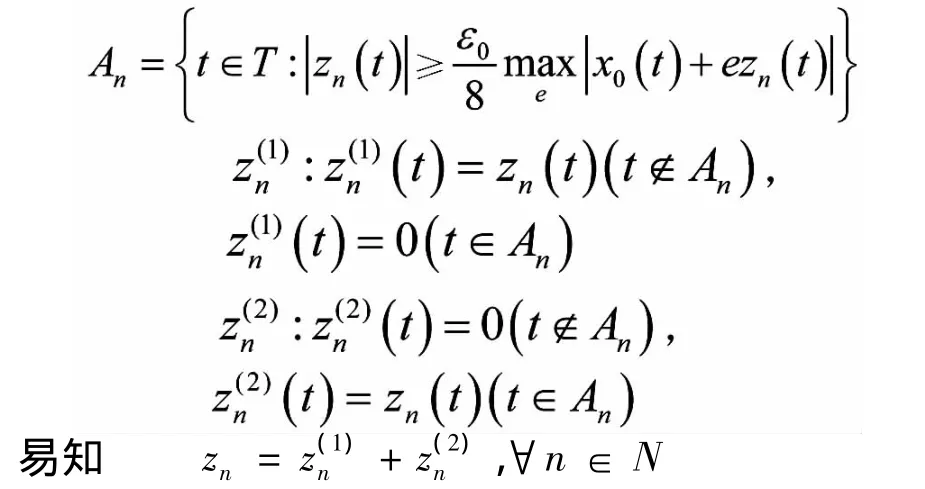
由于|λn|→1(n→∞)，可知对充分大的n有下式成立:

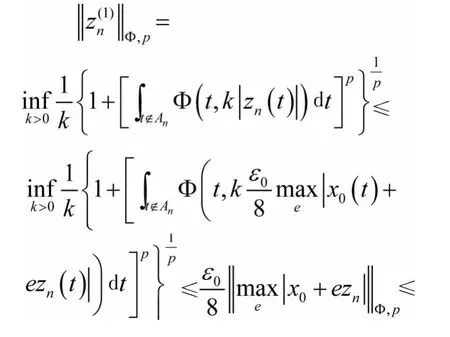
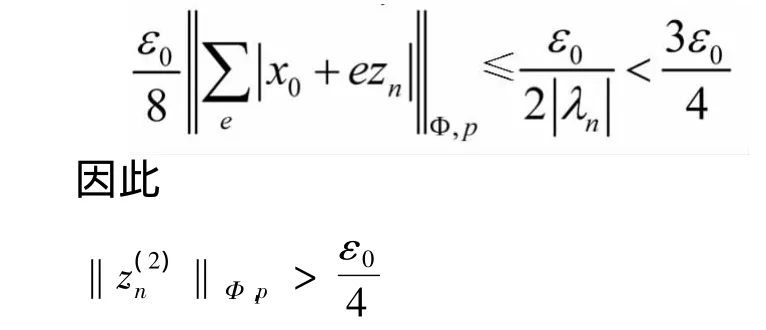
这说明An≠∅.从而，对任意t∈An，有

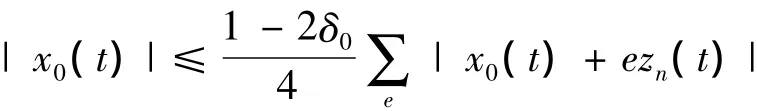
为完成证明，考虑如下两种情形:

(Ⅰ)kn→∞(n→∞)，这里

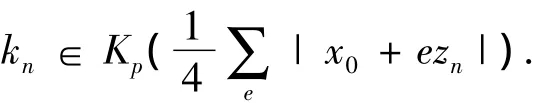
则对每个n∈N，

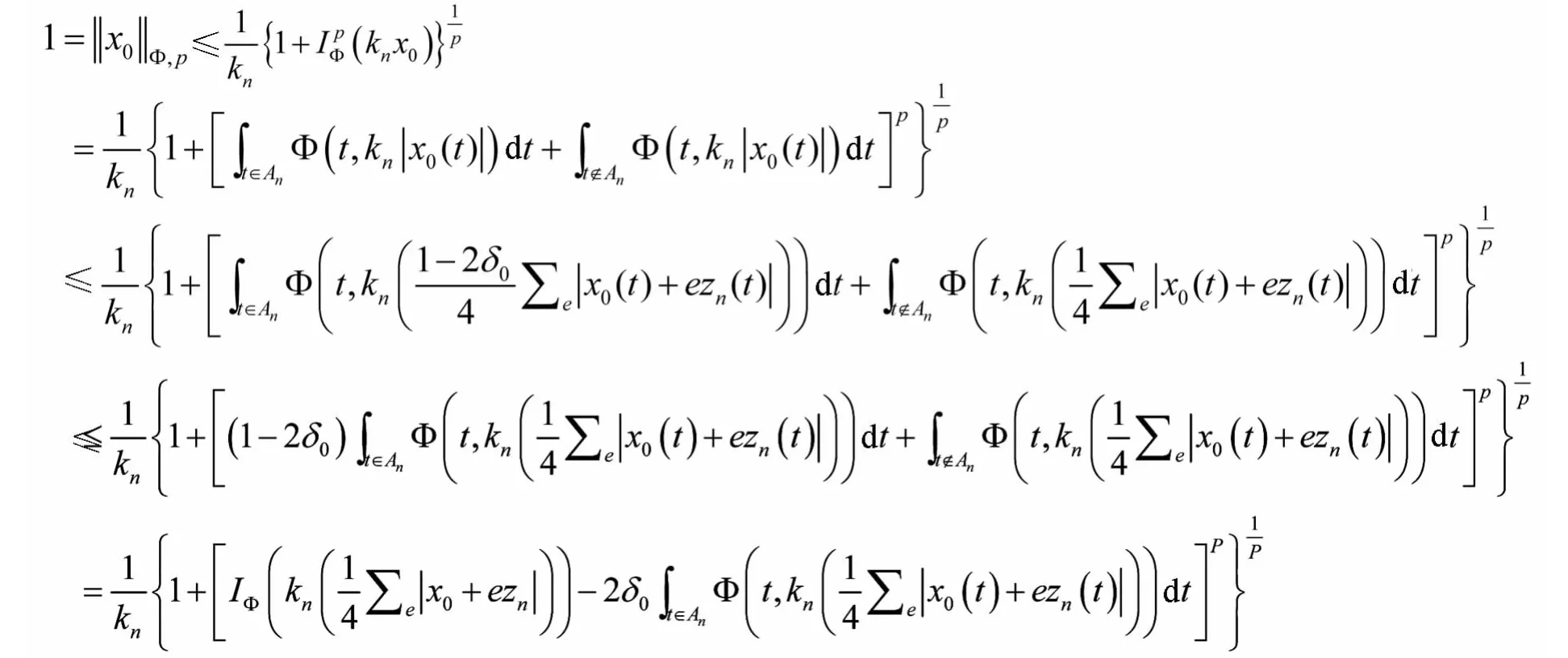
注意到

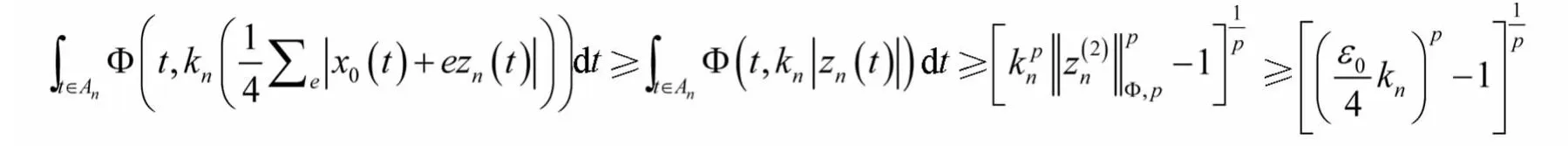
由于kn→∞(n→∞)，可知对充分大的n，有

考虑到p是奇数，可推出如下矛盾:

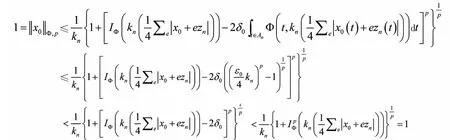
(Ⅱ)kn→k0(n→∞)，这里

则对每个n∈N，有

令n→∞，可知

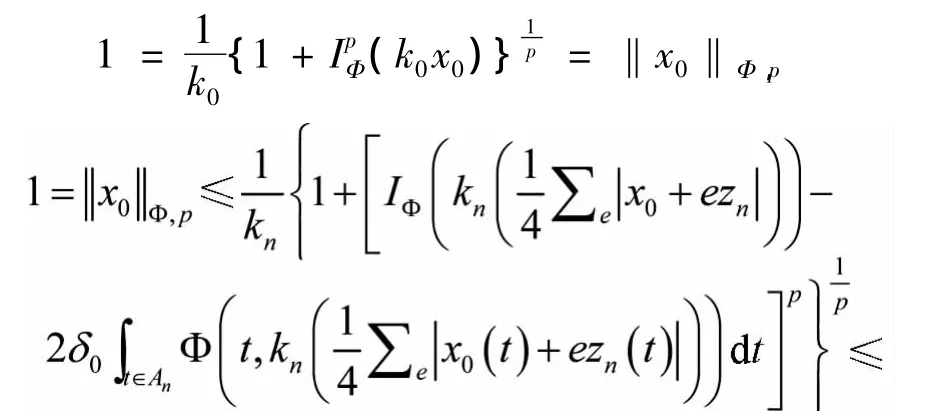
利用(Ⅰ)，知

因为kn→k0(n→∞)，故对充分大的n有如下不等式成立：

则

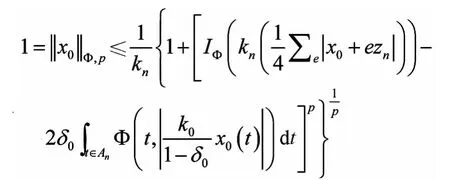
可知

又因p是奇数，得到如下矛盾:

定理证毕.

3 结束语

通过该文的研究，得到了赋p-Amemiya范数的Musielak-Orlicz函数空间中1≤p＜∞且p是奇数时，该空间中单位球的复端点和复强端点的判别准则.但是，当p为偶数的情况下，该空间中单位球的复端点和复强端点的判别准则尚未得出，这部分结果正在研究当中.

［1］ Thorp E，Whitley R.The Strong Maximum Modulus Theorem for Analytic Functions into a Banach Space［J］.Proc Amer Math Soc，1967，18(4):640-646.

［2］ 吴从炘，孙慧颖.关于Musielak-Orlicz空间的复端点与复严格凸［J］.系统科学与数学，1987，7:7-13.

［3］ 吴从炘，孙慧颖.Musielak-Orlicz空间的复一致凸性［J］.东北数学，1988，4:389–396.

［4］ Wu C，Sun H.On the Complex Convexity of Musielak-Orlicz Spaces［J］.Comment.Math，1989，28:397-408.

［5］ Cui Y，Duan L，Hudzik H，et al.Basic Theory of p-Amemiya Norm in Orlicz Spaces(1≤p≤∞):Extreme Points and Rotundity in Orlicz Spaces Equipped with These Norms［J］.Nonlinear Anal，2008，69(5-6):1796-1816.

［6］ Cui Y，Hudzik H，Li J，et al.Strongly Extreme Points in Orlicz Spaces Equipped with the p-Amemiya Norm［J］.Nonlinear Anal，2009，71(12):6343-6364.

［7］ Chen S T.Geometry of Orlicz spaces，Dissertations Math.Warszawa，1996.

［8］ Chen Lili，Cui Yunan，Hudzik Henrik.Criteria for Complex Strongly Extreme Points of Musielak-Orlicz Function Spaces［J］.Nonlinear Anal，2009，70(6):2270-2276.