ORLICZ-LORENTZ SEQUENCE SPACES EQUIPPE WITH THE ORLICZ NORM*

In memory of Henryk Hudzik, a great man, our teacher and colleague

Yunan CUI(崔云安)

Department of Mathematics，Harbin University of Science and Technology，Harbin 150080，China E-mail: cuiga@hrbust.edu.cn

Pawel FORALEWSKTJoanna KONCZAK

Faculty of Mathematics and Computer Science,Adam Mickiewicz University,Poznat,Uniwersgtetu Poznaniskiego 4，61-614 Poznani，Poland E-mail : katon @amu.edu.pl; jkonczak@amu.edu.pl

holds for any u ∈[0,u0] (then we also have aφ=0).

Given any Orlicz function φ, we define its complementary function in the sense of Young by the formula

for all u ∈R. It is easy to show that ψ is also an Orlicz function. The Orlicz function φ and its complementary function ψ satisfy the Young inequality

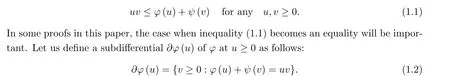
By l and p we denote the left and right derivative of φ respectively. Then we have that

(i) if u ∈[0,bφ); then ∂φ(u)=[l(u),p(u)],

(ii) if u=bφand l(bφ)＜∞, then ∂φ(bφ)=[l(bφ),∞);

(iii) if either (u=bφand l(u)=∞) or u>bφ, then ∂φ(u)=∅.

Let ω : N →R be a nonnegative, nontrivial and non-increasing sequence, called a weight sequence.

In the past research mainly Orlicz-Lorentz spaces equipped with the Luxemburg norm were studied (see [1, 4, 9-14, 20, 21, 25, 30, 36-38]). Recently, Orlicz-Lorentz spaces equipped with the Orlicz norm have been considered in some papers (see [15, 34] and also [6]). However,in those papers only some special cases of Orlicz functions and weight sequences have been investigated. In our paper we admit any Orlicz function and any non-increasing weight sequence.

Remark 1.1 Let φ be any Orlicz function and ω any nonnegative and nontrivial weight sequence. If aφ=bφ, then λφ,ω=l∞and ‖x‖φ,ω= ‖x‖Aφ,ω=‖x‖l∞/bφfor any x ∈λφ,ω. Let now aφ＜bφ. Then the following conditions are equivalent: the sequence ω is non-increasing,the second equality in formula(1.3)holds and the semimodular Iφ,ωis convex(see[11,Theorem 2.2]). The convexity of the semimodular Iφ,ωis in turn essential to prove that the functionals defined by (1.5) and (1.7) are norms. Also, the functional defined by (1.6) is a norm if the sequence ω is non-increasing.

2 Some Basic Results

We start with the following Lemma 2.1 For any x ∈λφ,ω, we have The function f is continuous on the interval (0,λ∞) and left continuous at λ∞if λ∞＜∞.

Let E ⊂l0be a normed Riesz space, that is, a partially ordered normed vector space over the real numbers, such that

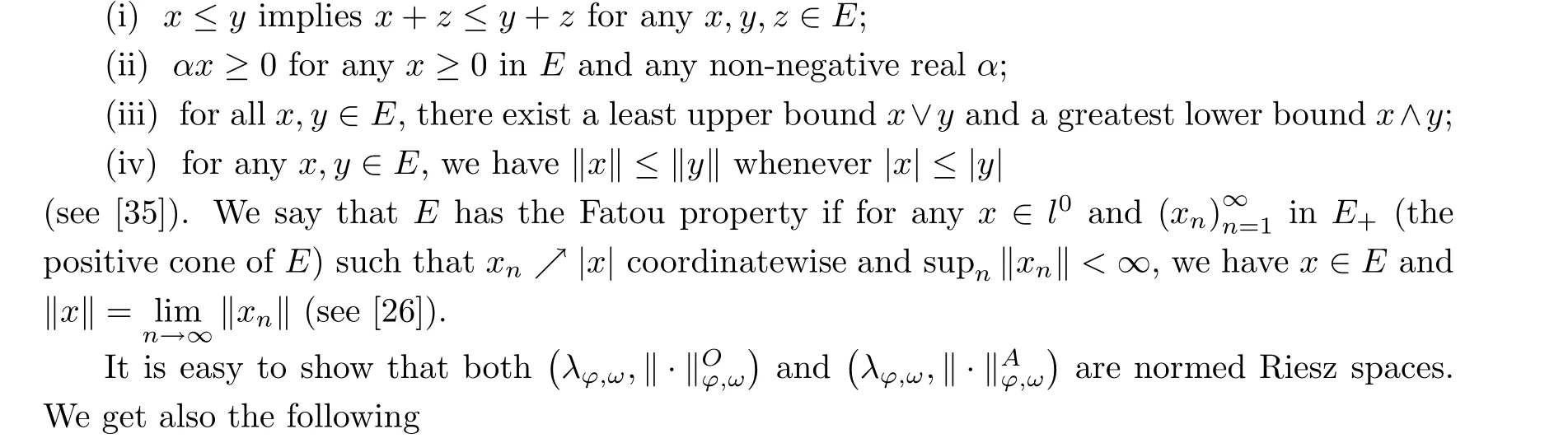
for any n ≥n1, we get a contradiction with (2.7). □

Theorem 2.3 The Orlicz and Amemiya norms are equal; that is, for any x ∈λφ,ω, we have

a contradiction. □

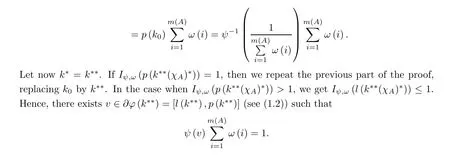
Proceeding analogously as above, we obtain again (2.16).

Case 2 Suppose now that bφ＜∞. Then k∗≤k∗∗≤bφ(see Remark 2.12). If k∗＜bφwe may again repeat the proof of Case 1 to get (2.16). Assume now that k∗= k∗∗= bφ. But then Iψ,ω(l(k∗∗(χA)∗)) ≤1 and we will find w ∈∂φ(k∗∗) = ∂φ(bφ) = [l(bφ),∞) (see (1.2))such that

Let E ⊂l0be a H K¨othe sequence space. An element x ∈E is said to be order continuous if for any sequence(xn)in E+(the positive cone of E)with xn≤|x| and xn→0 coordinatewise,there holds ‖xn‖E→0. The subspace Eaof all order continuous elements in E is an order ideal in E. The space E is called order continuous if Ea=E (see [26]).

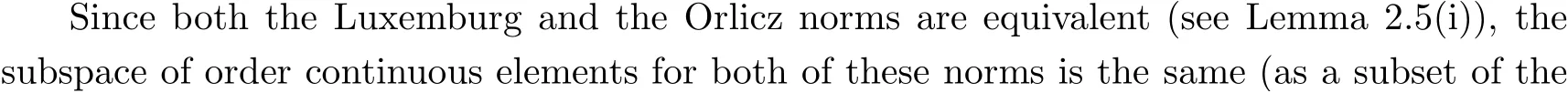
3 Monotonicity Properties and Copies of l∞

A Banach lattice E is said to be strictly monotone if x,y ∈E+(the positive cone of E),y ≤x and y /=x imply that‖y‖＜‖x‖(see[3]). E is said to be lower(upper)locally uniformly monotone, whenever for any x ∈E+with ‖x‖ = 1 and any ε ∈(0,1) (resp. ε > 0) there is δ = δ(x,ε) ∈(0,1) (resp. δ = δ(x,ε) > 0) such that the conditions y ∈E, 0 ≤y ≤x (resp.y ≥0) and ‖y‖ ≥ε imply ‖x-y‖ ≤1-δ (resp. ‖x+y‖ ≥1+δ) (see [18]). We say that E is uniformly monotone if for any ε ∈(0,1), there is δ(ε)∈(0,1) such that ‖x-y‖≤1-δ(ε)whenever x,y ∈E+, y ≤x, ‖x‖=1 and ‖y‖≥ε (see [3]).

Proof (i)⇒(ii). If aφ= 0, then the proof of this implication is analogous to the proof of sufficiency in Theorem 3.1. Let us now assume that aφ> 0. Then for any n ∈N we have K(xn) = ∅. Take any x,y ∈(λφ,ω)a, x ≥0, y ≥0, y /= 0. First we shall show that K(x+y) = ∅. Let us take any k > 0. Since (λφ,ω)a= c0, there exists n(k) ∈N such that k(x+y)∗(n)＜aφfor any n>n(k), whence

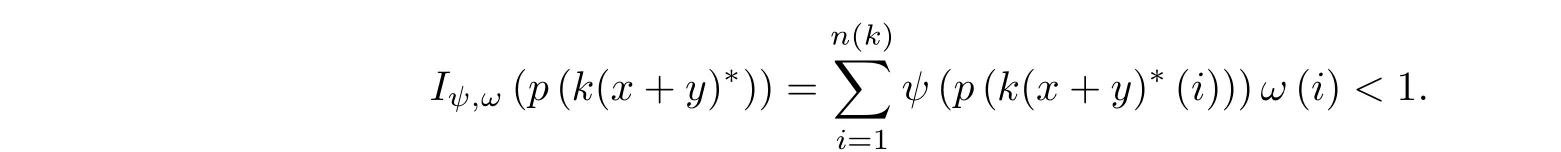
By the arbitrariness of k >0, we get K(x+y)=∅. Using again the fact that (λφ,ω)a=c0, we conclude that there exists j ∈N such that x∗(j)＜(x+y)∗(j). We will also find k0>0 such that

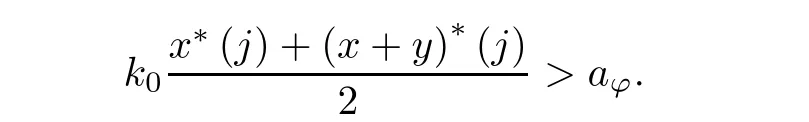
where the constant 0 ＜ν(ε)≤ε depends only on ε. Let p ∈N be the smallest natural number such that the inequality

holds, where η is the constant from the definition of the regularity of the weight function.

Let a1:=sup{i=1,2,...,m:x(i)=x(1)}. Then 1 ≤a1≤m and x(a1)>x(a1+1). If a1＜m, that means x(a1+1)>0, analogously as above we define a2,...,al,al=m in such a way that

4 Applications to Orlicz Sequence Spaces

Let us notice that in the case when ω(i)=1 for any i ∈N, Orlicz-Lorentz sequence spaces become the well-known Orlicz sequence spaces.

On the basis of the results obtained in the previous part of this paper, we easily get respective criteria for Orlicz sequence spaces lφas well as for their infinitely dimensional subspaces hφ(that is, subspaces of order continuous elements in lφ)and their n-dimensional subspaces lnφ(n ≥2).