一类新型抽象二阶积-微分方程两点边值问题

王 红 卫

(中国石油大学 理学院，山东 青岛 266580)

一类新型抽象二阶积-微分方程两点边值问题

王 红 卫

(中国石油大学 理学院，山东 青岛 266580)

利用新的积分和微分不等式研究了一类新型抽象二阶积-微分方程的两点边值问题解的存在唯一性，给出了解的隐式迭代序列和误差估计式.

积-微分方程；单调迭代方法；微分和积分不等式

考虑Banach空间E中非线性二阶积-微分方程两点边值问题：

(1)

其中：t∈I=[0，1]，x0，x1∈E，f，g∈C[I×E，E]，k(t，s)∈C[D，R+]，R+=[0，+)，D={(t，s)∈R2：0≤s≤t≤1}，k0=max{k(t，s)：(t，s)∈D}.

设E是实Banach空间，P是E中的一个锥，P在E中定义半序“≤”，即：x，y∈E，x≤y⟺y-x∈P.

称Banach空间E中的锥P为正规的，如果θ≤x≤y，则‖x‖≤NP‖y‖，其中NP称为P的正规常数.设E*是E的共轭空间，P*={φ∈E*|φ(x)≥0，∀x∈P}称为P的共轭锥，显然有x∈P⟺∀φ∈P*，φ(x)≥0.

由文献[1]知，不失一般性，设正规常数NP=1.

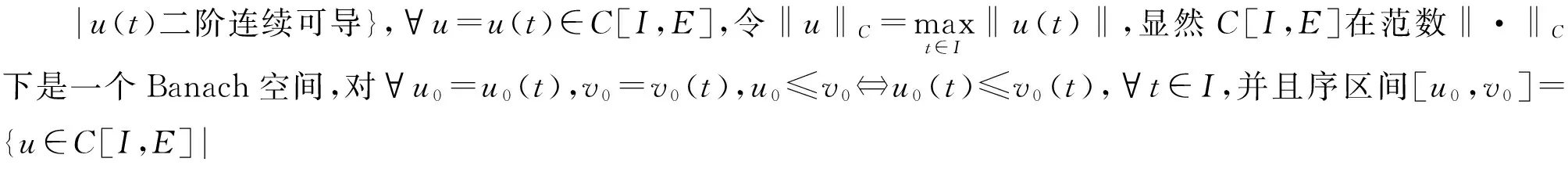
文献[2][3]讨论了两点边值问题解的存在性，但这些结果无一不使用了空间的某些紧性条件，并且没有给出解的迭代逼近和相应的误差估计.目前，关于两点边值问题(1)的研究并不多见，而有关的研究中同样也用到了某种紧性条件，并且不能得到解的存在唯一性及逼近解的迭代序列的误差估计.

此处是在没有使用任何紧性条件的前提下，利用单调迭代方法和积-微分不等式理论研究Banach空间中一类新型非线性二阶积-微分方程两点边值问题的解的存在性和唯一性，并且给出了单调收敛迭代序列和误差估计式.

1 引 理

引理1 设E是实Banach空间，P是空间E中的锥，u∈C2[I，E]，若存在常数M>0使得

u″≤Mu(t)，u(0)≥θ，u(1)≥θ

成立，则u(t)≥θ，t∈I.

引理2[4]设x(t)：I→E连续，则对任意的a∈I，下面成立：

显然有下面命题：

2 主要结果及证明

方便起见，列出下面的基本假设：

(H1) (i)存在u0∈C2[I，E]，使得下式成立：

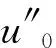
(ii)存在v0∈C2[I，E]，使得下式成立：

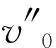
(H2) (i) 当t∈I，u，v∈G={w∈C[I，E]：w≥u0}，u≥v时，成立：

(ii) 当t∈I，u，v∈Q={w∈C[I，E]：w≤v0}，u≥v时，成立：

这里M>0，Li>0(i=1，2)是常数，且满足M<1，M+L1+L2k0<6成立.

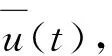
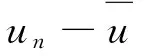
(2)

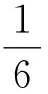
(3)

证明对任意的un-1∈C[I，E]，由M<1可知积分方程(3)存在唯一的解：un∈C[I，E].由式(3)可知：

(4)

下面证明：

un-1≤un，n=1，2，…

(5)

由式(4)和条件(H1)(i)可知，

(u1-u0)″(t)≤M(u1-u0)(t)

(u1-u0)(0)≥θ，(u1-u0)(1)≥θ

于是，根据引理1可知(u1-u0)(t)≥θ，t∈I，即u0≤u1.

假设uk-1，uk∈G，uk-1≤uk成立，由式(4)和条件(H1)(i)可知：

(uk+1-uk)″(t)≤M(uk+1-uk)(t)

(uk+1-uk)(0)≥θ，(uk+1-uk)(1)≥θ

于是，根据引理1可知，(uk+1-uk)(t)≥θ，t∈I，即uk≤uk+1.

因此，由数学归纳法可知式(5)成立.

由式(5)可知

u0≤u1≤u2≤…≤un≤…

(6)

由式(6)，条件(H2)(i)和引理2可知

于是得到：

⋮

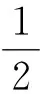
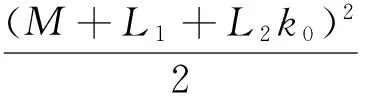
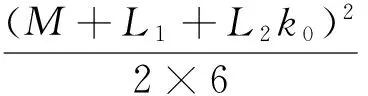
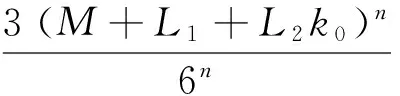
(7)

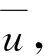
在式(3)中令n→，可以得到：

设v∈G也是边值问题(1)的解，则式(8)成立：

(8)

由式(4)(8)，条件(H1)(i)，条件(H2)(i)及引理1，利用数学归纳法可以证得：

un≤v，n=1，2，…

(9)

在式(9)中，令n→，并注意到锥P的正规性可知v.

⋮

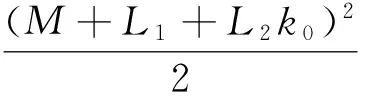
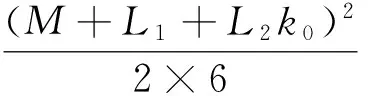
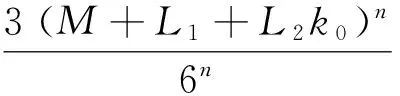
即

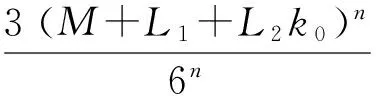
令n→，可以得到

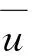
在式(7)中，令m→，可得近似解误差估计式(2).证毕.

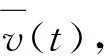
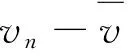
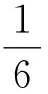
(10)

证明证明过程类似于定理1.

注1 利用半序理论与单调迭代方法研究各类积-微分方程解的存在性时，一般假设所研究的方程同时具有某种类型的上解和下解，而此处只利用了一个上解或只利用了一个下解，并且在较弱条件的前提下，讨论了一类新型的二阶积-微分方程，得到了较好的结果，与先前研究所得到的相关结果相比较，存在着本质性的改进和推广.

[1] GUO D J，LAKSHMIKANTHAM V. Nonlinear Problems in Abstract Cones [M].New York：Academic Press，Inc，1988

[2] GUO D J，LAKSHMIKANTHAM V. Multiple solutions of two-point boundary value problems of ordinary differential equations in Banach space [J].J Math Anal，1988(129)：211-222

[3] 宋福民. Banach空间中两点边值问题的解[J].数学年刊 ，1993，14A(6)：692-697

[4] 宋光兴.Banach空间积-微分方程两点边值问题[J].数学学报，2000，43(3)：555-560

[5] 宋光兴.Banach空间中两点边值问题解的存在唯一性[J].数学物理学报，1999，19(2)：159-164

[6] 张石生，王凡.Banach空间中二阶常微分方程的两点边值问题解的存在性定理[J].应用数学和力学，1996，17(2)：95-103

[7] 匡继昌.常用不等式[M].长沙：湖南教育出版社，1993

[8] 郭大钧，孙经先.Banach空间常微分方程理论的若干问题[J].数学进展，1994，23(6)：492-502

Two-point Boundary Value Problem for a Class of Novel Abstract Second-order Integrodifferential Equations

WANGHong-wei

(School of Science, China University of Petroleum, Shandong Qingdao 266580, China)

The existence of the uniqueness of the solution to two-point boundary value problem for a class of novel abstract second-order integrodifferential is studied by using new integral and differential inequality, the implicit iterative sequence and error estimation for the solution are given.

integrodifferential equation；monotone iterative method；integral and differential inequality

1672-058X(2013)09-0034-05

2013-04-10；

2013-05-20.

王红卫(1986-)，男，山东人，硕士研究生，从事非线性泛函分析及其应用研究.

O175.8

A

责任编辑：李翠薇