高斯-谢尔模光束在大气湍流中传输的相干特性研究*

李成强1)2)† 张合勇1)王挺峰1)刘立生1)2)郭劲1)

1)(中国科学院长春光学精密机械与物理研究所,激光与物质相互作用国家重点实验室,长春 130033)

2)(中国科学院大学,北京 100049)

1 引言

长久以来,激光相干特性和激光束的方向性被认为是直接关联的.然而,在1970年前后,理论和实验证明激光束方向性好并不意味着空间相干性高,这一发现引起了对部分相干光源的研究热潮[1].在部分相干光源中,有一种比较特殊的光源被称为高斯-谢尔源,因为该光源产生的光束远场光场强度分布和完全相干高斯光束一样[2].相干光在湍流介质中传输时,湍流会增加波前的随机性,使相干光以部分相干光的形式存在[3].另外,激光器自身因素往往造成激光束以多模的形式存在,多模激光辐射以部分相干的高斯-谢尔模型(GSM)光束形式存在[4].因此,对部分相干光的研究具有一定的实际意义.鉴于激光的应用需求,有必要阐明部分相干光源在湍流介质中的传输特性.目前的研究工作侧重于分析湍流介质对激光强度分布、空间相干性和偏振特性的影响[5-14].横向相干长度(相关长度)是空间相干性的直接反映,因此,对相干长度变化的研究有助于理解激光传输时空间相干特性及偏振特性的变化.Wu和Boardman[15]分析了相干长度、光源尺度同量级的GSM光束的传输特性,研究结果表明,光束在真空中传输时,其横向相干长度会缓慢增加,而在湍流中的传输会造成横向相干长度的减小.Friberg和Sudol[9]讨论了GSM光束在真空中传输时空间相干特性的变化,研究发现对于GSM光束,在真空中传输时横向相干长度与光斑尺度比值恒定不变.为保证部分相干光源的部分相干性,通常相干长度比光源尺度具有更小数量级[16],且研究大气湍流对相干长度的影响有必要排除光源扩展的影响.Friberg在讨论相干长度的变化时,虽排除了光源扩展的影响,但文章只讨论了光束的真空传输.出于应用需求考虑,有必要对湍流中部分相干光的传输做进一步分析.

本文以GSM光束为对象,根据广义惠更斯-菲涅耳原理推导出该光束传输时的交叉谱密度函数表达式,并根据该表达式分析了GSM光束传输时横向相干长度的变化情况,讨论了光源参数和湍流介质对横向相干长度变化所起的作用.在研究大气湍流对相干长度的影响时,为排除光源扩展的影响,分析了GSM光束在湍流介质中传输时横向相干长度与光斑尺度的比值,由此得出有助于部分相干光大气传输理论分析和实验的一些推论.

2 理论分析

将光场视为随机场u(r,ω),该随机场可以用平稳随机过程理论进行分析,其交叉谱密度函数定义为[5]

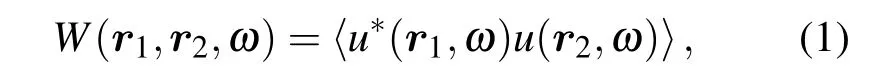
式中星号表示复共轭,尖括号表示系宗平均.对于给定的光源交叉谱密度W(0)(ρ1,ρ2;ω),根据广义惠更斯-菲涅尔原理可以得到任意平面(z=const)上T1=(r1,z＞0),T2=(r2,z＞0)两点处的交叉谱密度函数[5]:

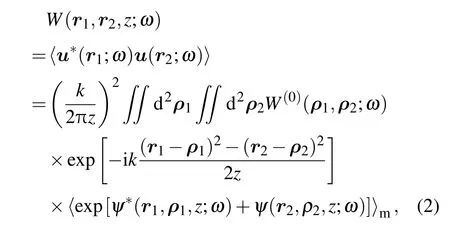
上式中,〈···〉m记为湍流介质的统计平均,并对其做如下近似[17]:

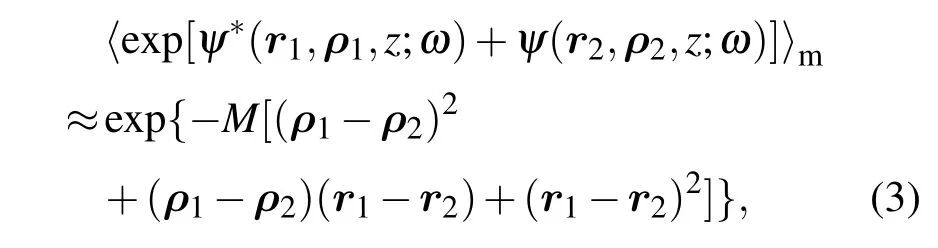
其中M为

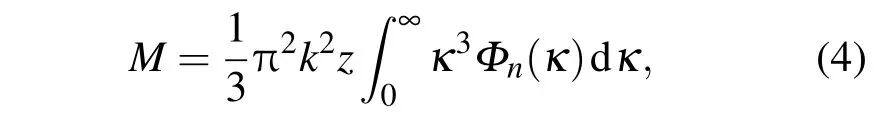
式中Φn(κ)为折射率波动的功率谱,本文选用Tatarski谱[5]:

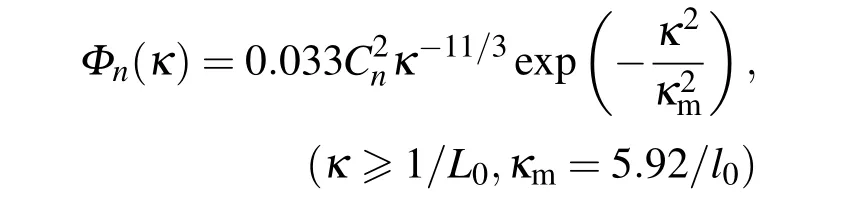
其中l0,L0分别表示湍流内尺度和外尺度,为折射率结构常数.

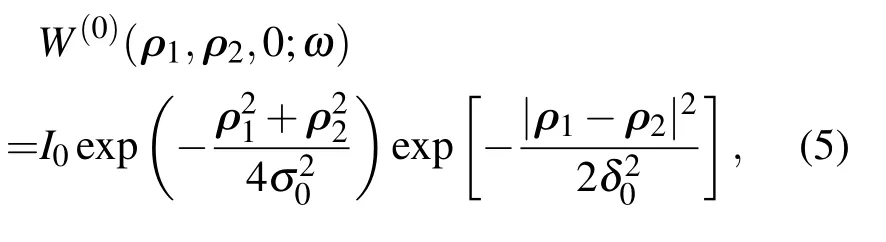
现在考虑具有高斯型光强分布和相干性分布的高斯-谢尔源产生的随机光场.光源面处交叉谱密度可表示为[18]上式中,参数I0及σ0,δ0分别为光源的光强、光斑尺度和相干长度.一般来说,为了保证光束具有部分相干特性,相干长度δ0的值要比光斑尺度σ0小得多,通常它们不在一个数量级上[16].

将(5)式及(3)式代入(2)式,可得

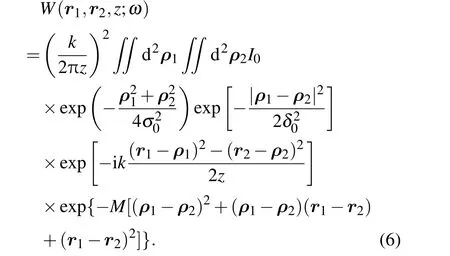
对上式进行冗长的积分运算,可得高斯-谢尔光束传输时交叉谱密度函数W(r1,r2,z;ω)的表达式:

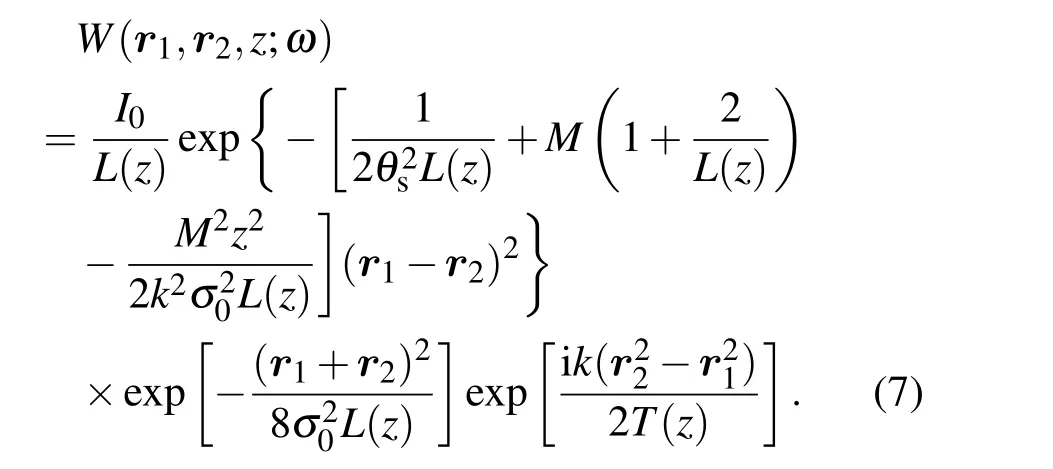
上述表达式在交叉谱密度定义及湍流理论的基础上,经过相应数学自主运算而获得,其中相应参数如下:

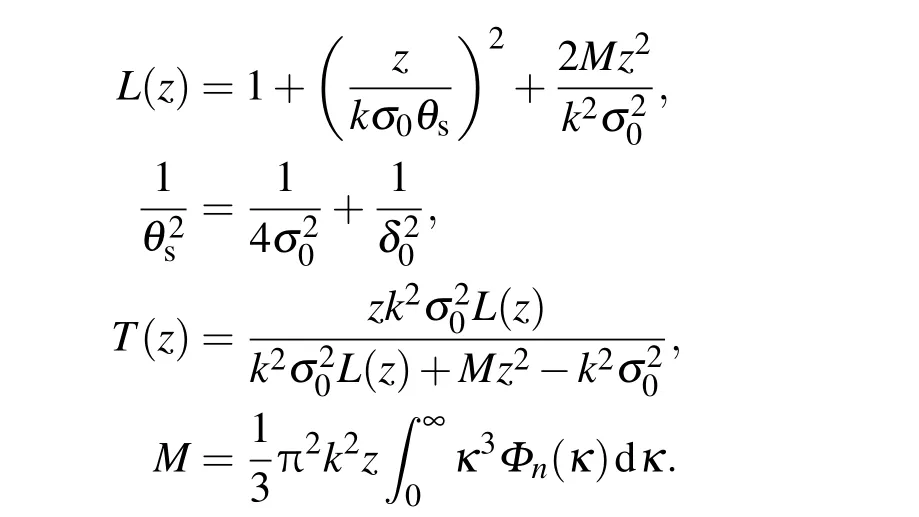
复相干度的表达式[19]:

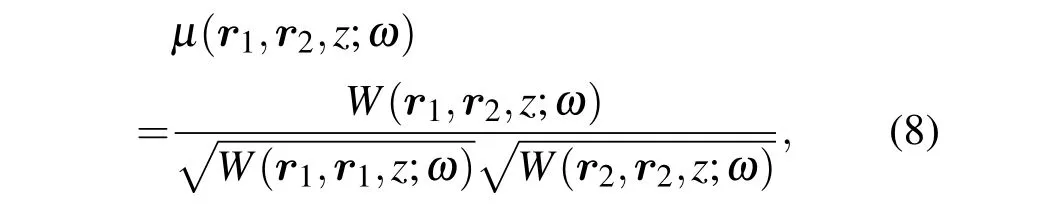
将(7)式代入(8)式整理可得:

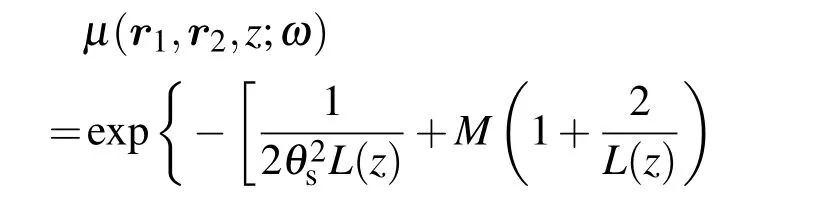
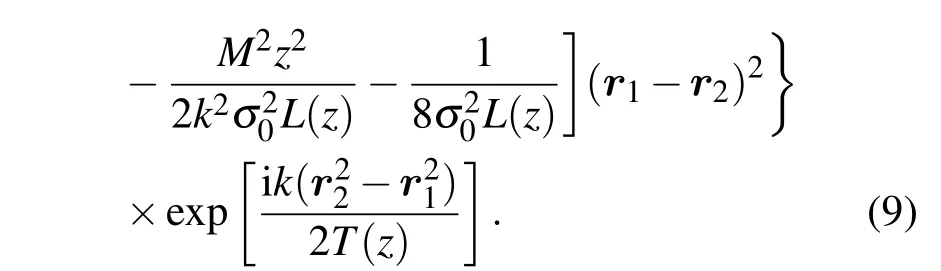
考虑复相干度的幅值,令

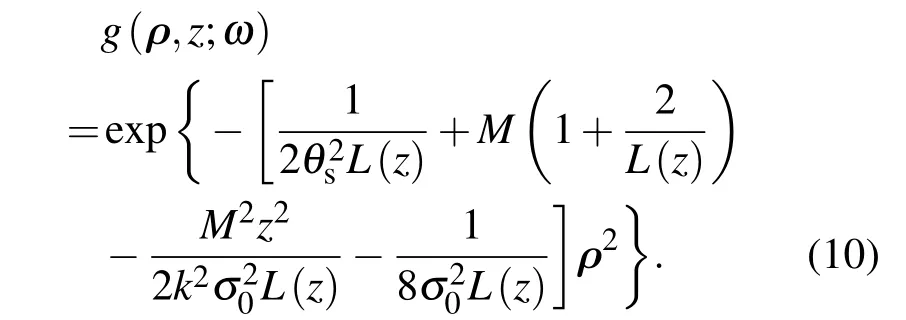
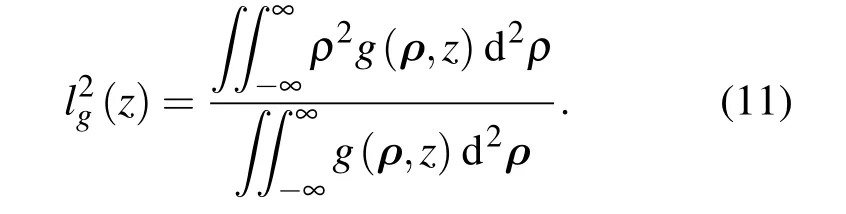
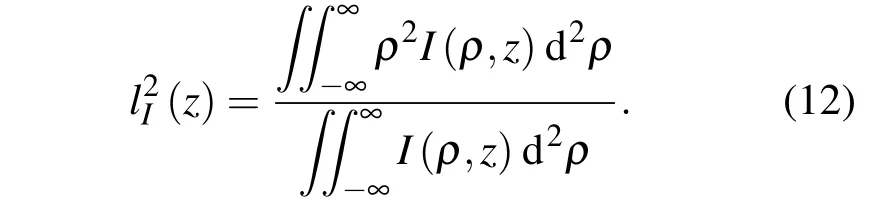
传输路径上,平面z≥0处的光强度为

据此,可得

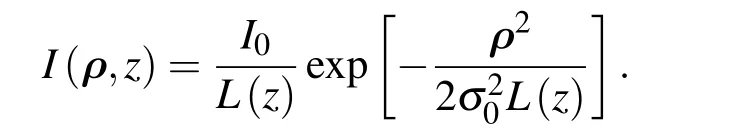
通过自主推导的交叉谱密度函数表达式,可得相干长度和光斑尺度的平方,计算得相干长度的平方为

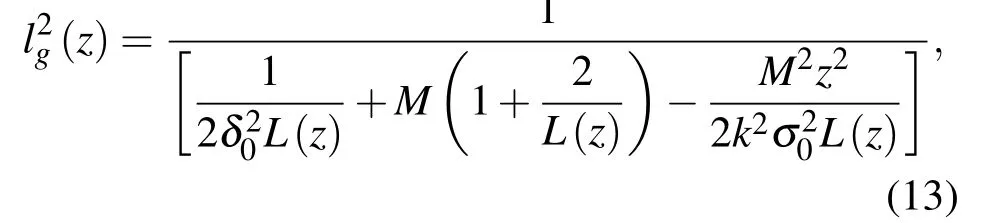
光斑尺度的平方为

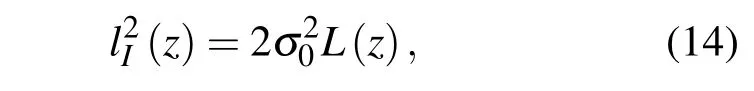
光束在真空中传输时,光斑尺度为

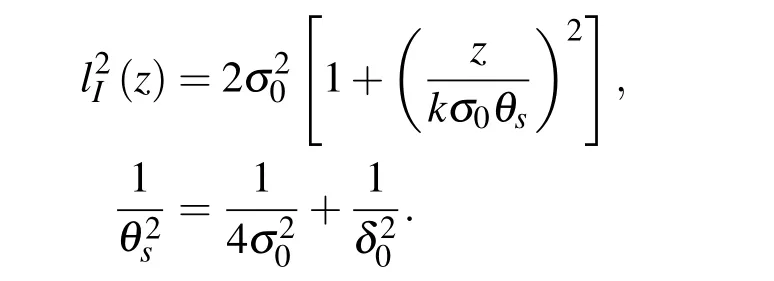
由上式可以看出,真空传输时光束扩展与σ0,δ0有关,光束扩展快慢主要由δ0决定.相干长度与光斑大小的比值α2[9]:

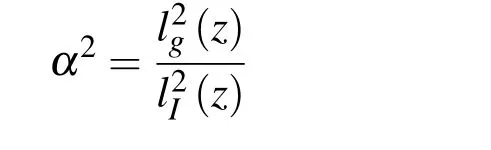
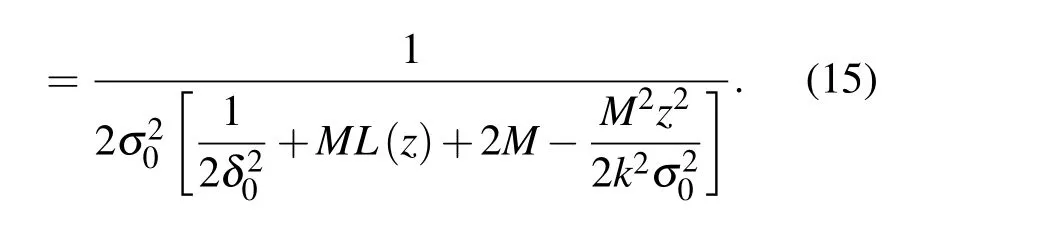
由(15)式可以看出,相干长度与光斑尺度的比值α与光源参数、湍流强度及传输距离有关,真空传输时,比值α为一确定值,这与Friberg研究GSM光束真空传输所得结果一致.但Friberg未对湍流中的光传输予以讨论,本文将对这一传输问题进行分析.

3 数值计算结果与分析

通过表达式(13)可以看出,光源参数和湍流因素同时影响光传输时相干长度的变化.本文将对具有不同光源参数的光束在不同湍流条件下的传输进行数值计算,并给出理论分析.数值计算时参数的选取:湍流内尺度l0=5 mm,波数k=2π/λ=107.

图1为光束在真空中传输时相干长度和光斑尺度的变化.图1(a),(c)表明真空中传输时,对确定光源,相干长度和光斑大小随传输距离线性增加;图1(a),(b)反映了真空中光源参数对相干长度的影响,相干长度随传输距离变化的快慢与光源大小有关,光源尺度σ0越大,相干长度增加越慢;图1(c),(d)则反映了光源参数对光源扩展的影响,光源扩展的快慢主要由光源相干长度δ0决定,相干长度小的光源扩展快.

图2为光束在湍流中传输时,相干长度和光斑尺度随传输距离的变化.在湍流中,光源尺度及湍流强度对相干长度的影响较大,而光源相干性影响较小.由图2(a),(e)可以看出,湍流中相干长度在传输距离较短时基本为线性增加,当传输距离较大时,相干长度随着传输距离的增加而缓慢减小.对光束扩展的分析表明,湍流和光源相干性影响较大,而光源尺度对湍流中光束扩展影响较小.图2(d),(f)表明光源相干性越差、湍流越强,传输过程中光束扩展越严重.通过以上分析可知,相干长度的变化受到光源参数和湍流强度的共同影响,其中光源参数的影响体现在光束扩展上.因此单纯地分析相干长度的变化不足以反映光源参数和大气湍流对光传输的影响.为排除光束扩展的影响,将利用相干长度和光斑尺度的比值进行分析.

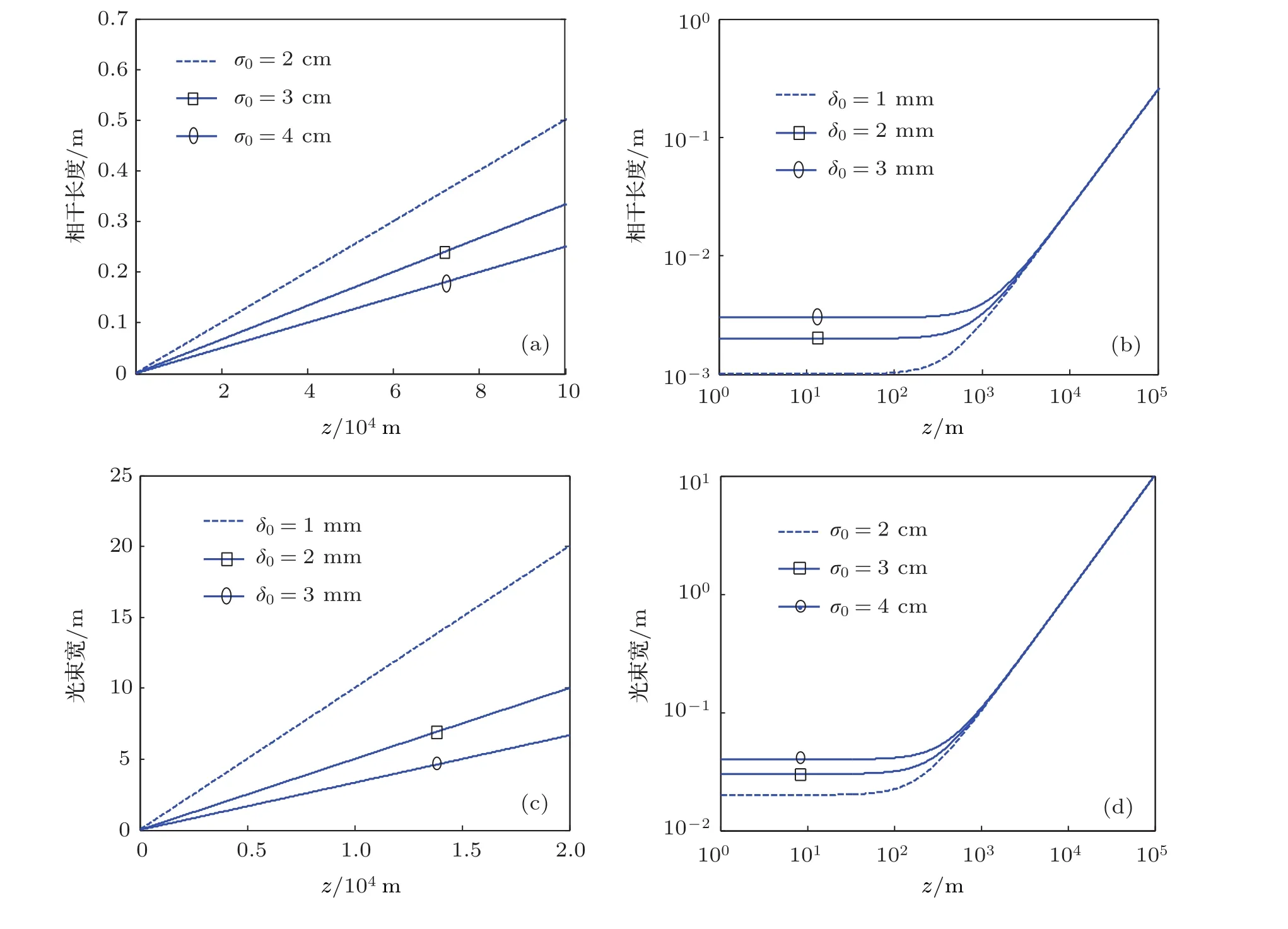
图1 真空中相干长度及光斑大小的变化(=0)(a)δ0=1 mm;(b)σ0=4 cm;(c)σ0=4 cm;(d)δ0=1 mm

图3为光束在湍流中传输时相干长度与光斑尺度的比值随传输距离的变化,结果表明:光束在湍流中传输时,对参数不同的光源,相干长度和光斑大小的比值均会减小;真空传输时,相干长度与光斑尺度比值为确定值,而当湍流存在时,相干长度与光斑尺度的比值同时受到光源参数和湍流强度的影响,该比值不再是一个确定的值;传输距离较小时,由于湍流影响小,此时与真空传输类似,比值α变化很小,当传输距离较大时,湍流影响明显,比值α随传输距离的增加而下降.图3(a)中=10-14m-2/3,δ0=1 mm,通过改变比值β改变光源尺度大小,发现α的值在光传输一段距离后趋于一致;图3(b)中=10-14m-2/3,σ0=4 cm,通过改变比值β改变光源相干长度大小,发现只有当光传输距离很远时α的值才有可能趋于一致;图3(c)中光斑尺度与相干长度比值不变,光传输一段距离后,相同位置处α的值会随着光源尺度和相干长度的增加而增大.如果将传输过程中α的值发生较大变化的位置记为zc,通过图3(d)可以发现,对确定的光源,zc的值会随着湍流强度的增加而减小.

产生以上结果的主要物理原因是光束在湍流介质中传输时,光束波前会受到湍流影响,使波前随机性增大,湍流越强,光束的波前受到的影响也将越明显,波前随机性将削弱原有波前相位的关联性,而光波前相位的关联性直接影响光束的相干性.因此,光束在湍流介质中传输时会因为湍流的作用而引起相干性下降.具有部分相干性的光束,其原有波前即具有一定的随机性,但这种随机性并不能减小湍流对光束现有波前的影响,因为湍流效应由湍流强度和传输距离共同决定,湍流引起的波前变化与光束原有波前相互独立.光束在真空中传输时,自由衍射引起光束扩展,相干长度的变化受光束扩展影响而增加,这一点可以通过图1看出.光束在大气湍流中传输时相干属性的变化由光源参数和湍流强度共同决定.当光束在湍流介质中传输距离较短时,湍流作用很小,以至于对光束引起的波前随机性可以忽略.光源参数对光传输的影响占有主要地位,在这一距离内以自由衍射作用为主,光束扩展引起相干长度的增加,此时与自由空间传输类似,这一点可以由图2(a),(e)看出.但随着传输距离的增加,湍流效应增强并造成相干长度下降.

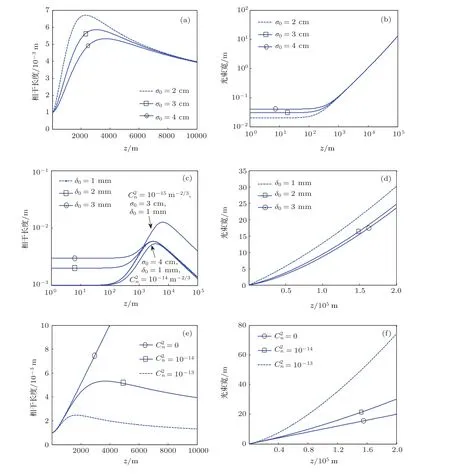
图2 湍流中相干长度及光斑大小的变化 (a),(b)10-14m-2/3,δ0=1 mm;(c),(d)=10-14m-2/3,σ0=3 cm;(e),(f)δ0=1 mm,σ0=4 cm

4 结论

本文以部分相干的GSM光束为对象,根据广义惠更斯-菲涅耳原理推导出GSM光束传输时交叉谱密度函数的解析表达式.基于该表达式数值分析了大气湍流对相干长度的影响,并与真空中传输相干长度的变化做了对比,发现GSM光束在真空中传输时,影响相干长度变化的因素为光源参数,光束扩展造成相干长度增加,自由空间中光束扩展是光束自由衍射的结果;而在大气湍流中传输时,相干长度的变化受光源参数和湍流的共同影响,结果表明,在传输距离较短时,光束传输特性与真空传输类似,相干长度因为光束扩展而增加,当传输距离较大时,湍流效应增强引起相干长度下降.因此,单纯从相干长度方面分析大气湍流带来的影响不够完备.为排除光源扩展的影响,本文利用相干长度与光斑尺寸的比值进行分析,发现对参数不同的光源,大气湍流均会造成比值的下降,但比值下降的快慢与光源参数和湍流强度有关.上述结论不仅可以用于分析激光传输时的相干度问题,还可以用于普通的电磁光束传输领域.

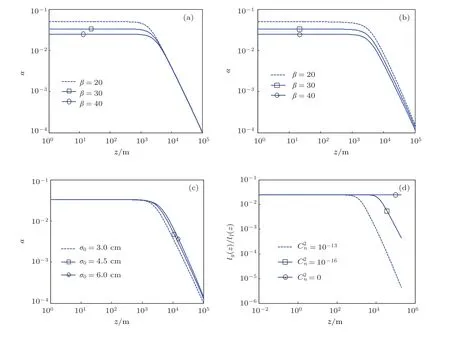
图3 相干长度与光斑大小的比值(β=σ0/δ0)(a)=10-14,δ0=1 mm;(b)=10-14m-2/3,σ0=4 cm;(c)=10-14m-2/3,β=30;(d)σ0=4 cm,β=40

[1]Shirai T,Wolf E 2002 Opt.Commun.20425

[2]Deschamps J,Courjon D,Bulabois J 1983 J.Opt.Soc.Am.73256

[3]Jian W 1990 J.Mod.Opt.37671

[4]Gase R 1991 J.Mod.Opt.381107

[5]Andrews L C 2005 Laser Beam Propagation through Random Media(Washington:SPIE)p67,pp500–510

[6]Clifford S E,Gracheva M E,Ishimaru A 1978 Laser Beam Propagation in the Atmosphere(New York:Springer)pp129–168

[7]Andrews L C 2001 Laser Beam Scintillation with Applications(Washington:SPIE)pp1–60

[8]Collett E,Wolf E 1978 Opt.Lett.227

[9]Friberg A T,Sudol R J 1983 Opt.Acta:Int.J.Opt.301075

[10]Salem M,Korotkova O,Dogariu A,Wolf E 2004 Waves in Random Media 14513

[11]Korotkova O,Salem M,Wolf E 2004 Opt.Commun.233225

[12]Cheng K,Lü B D 2009 Acta Phys.Sin.58250(in Chinese)[程科,吕百达2009物理学报58250]

[13]Ji X L,Li X Q 2009 Acta Phys.Sin.584624(in Chinese)[季小玲,李晓庆2009物理学报584624]

[14]Lü S Y,Lü B D 2009 Chin.Phys.B 183883

[15]Wu J,Boardman A D 1991 J.Mod.Opt.381355

[16]Mandel L,Wolf E 1995 Optical Coherence and Quantum Optics(Cambridge:Cambridge University Press)p279

[17]Roychowdhury H,Ponomarenko S A,Wolf E 2005 J.Mod.Opt.521611

[18]Lü B D 2003 Laser Optics:Beam Characterization,Propagation and Transformation,Resonator Technology and Physics(Beijing:Higher Education Press)p203(in Chinese)[吕百达2003激光光学:光束描述,传输变换与光腔技术物理(北京:高等教育出版社)第203页]

[19]Born M,Wolf E 2005 Principles of Optics(Cambridge:Cambridge University Press)p564

[20]Collett E,Wolf E 1980 Opt.Commun.3227

[21]Foley J T,Zubairy M S 1978 Opt.Commun.26297