利用超相对论量子分子动力学模型研究交变梯度同步加速器能区Au+Au碰撞中的核阻止效应*
袁颖
(广西师范学院物理与电子工程学院,南宁 530023)
1 引言
超相对论能区重离子碰撞为研究极高温度、密度条件下的强反应物质提供了机会[1-4].在高能核碰撞中会形成反应粒子的强激发体系[5].在此条件下夸克-胶子等离子体将会形成,可以利用输运模型研究热密核物质的许多基础特性.目前输运模型有很多,目的都是为了对粒子和核物理实验中粒子探测器得到的末态强子分布进行准确模拟[6].
人们试图从重离子碰撞数据中获得热密核物质的性质,这就需要对核阻止信息进行深入研究.事实上,人们可以通过研究反应末态的碎块(或者自由核子)在横、纵方向的快度分布来获得核阻止信息[7].
为了研究核阻止效应,本文首先简要介绍超相对论量子分子动力学(UrQMD)模型、核子-核子弹性散射反应截面的介质修正以及新的碎块形成判断条件.其次,将利用此模型得到的理论计算结果与实验数据进行比较.研究表明,考虑了上述条件后,UrQMD模型能够很好地描述交变梯度同步加速器(AGS)能区的自由质子快度分布.
2 超相对论量子分子动力学模型
UrQMD模型是一种基于所有重子在轨道上协变传播的微观输运理论[8].UrQMD模型给出了一系列耦合积分-微分方程的Monte Carlo解,这些方程是各种粒子(N,Δ,Λ等)的相空间密度随时间的演化[9].该模型主要用于描述德国重离子同步加速器(SIS)能区、美国相对论重离子对撞机(RHIC)能区和瑞士大型强子对撞机(LHC)能区的质子-质子、质子-核、核-核碰撞[10].它合并了不同的反应机制,能够给出各种实验观测量的理论模拟结果.一般而言,在研究强子的输运过程时,需要考虑粒子的平均场势、两体散射反应截面[11]和碎块的形成判断条件三个因素.
2.1 平均场势
与量子分子动力学模型相同,UrQMD模型也是基于平行原则.在相空间中,强子用高斯波包表示,并根据下列哈密顿运动方程来传播[12]:


在标准UrQMD模型中,势能U包括两体Skyrme项、三体Skyrme项、Yukawa项、Coulomb项和Pauli项[8,12],即

在高能区,重子的Yukawa势、Pauli势和对称势可以忽略,但Skyrme势和动量相关项仍然影响着重离子碰撞的整个动力学过程[13].在强子的形成过程中,“预形成”粒子被认为是自由流,且减小的反应截面也仅仅是对领头强子而言的.在考虑了形成和“预形成”粒子的平均场势后,UrQMD模型的理论计算结果与实验结果符合得很好[10,14].
2.2 核子-核子弹性散射反应截面的介质修正
在AGS能区,除了考虑平均场势的修正外,还需考虑两核子间反应截面的介质修正.本文只考虑了弹性散射反应截面的介质修正,非弹道仍采用实验上自由空间的反应截面.共考虑了核子-核子弹性散射反应截面的σfree和两种形式.这里σfree为自由的核子-核子弹性散射反应截面;为介质修正后的核子-核子弹性散射反应截面[15],
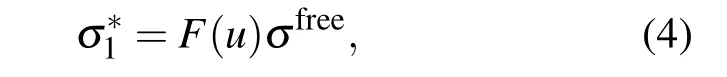
其中介质修正因子F依赖于核缩减密度u,即

这里ξ=0.5,u=ρi/ρ0,且不考虑动量约束.
2.3 新的碎块形成判断条件
在中低能区,碎块形成的判断条件通常有两种形式.一种是最小生成树(minimum spanning tree,MST)模型:dr<3.0 fm,dp<0.2,其中,dr=-为两核子相对距离,dp=-为两核子相对动量.另一种是同位旋依赖的最小生成树(Isospin dependent minimum spanning tree,Iso-MST)模型[16]:drpp<=3 fm,drnp,nn<=6 fm,dp<0.25 GeV/c,其中,,和分别为质子-质子、质子-中子和中子-中子间相对距离.
由兰州大学王永佳在2012年超重核合成机制与性质研讨会上的报告可知,在反应条件相同的情况下,随着入射能量的增加,运用这两种判断条件后自由质子的产额越来越接近,说明在高能区这两种判断条件给出的结果相似.
所以,在AGS能区本文采用MST模型的碎块形成判断条件,即 dr<5.0 fm,dp<0.5 GeV/c.同时得到的自由质子产额为=,其中,Nfreep为运用碎块形成条件判断后UrQMD模型计算得到的自由质子产额,为最终计算得到的自由质子产额,α为减小因子.在此模型中,α由理论计算结果与实验结果拟合得到.
3 AGS能区自由质子快度分布
由于实验上没有提供在高能区粒子的横向快度分布,所以一般仅采用粒子的纵向快度分布来描述核阻止效应[10].Yuan等[10]发现,加入形成和“预形成”粒子的平均场势后模型的计算结果在中心快度区比实验结果高.因此,本文考虑在UrQMD模型(3.3版)中加入形成和“预形成”粒子的平均场势、核子-核子弹性散射反应截面的介质修正和新的碎块形成判断条件.
图1所示为2A GeV的Au+Au中心碰撞(σ/σT<5%)产生的自由质子快度分布.这里2A GeV表示实验中单个入射核子的能量为2 GeV,σ为射弹与靶的反应截面,σT为总反应截面.图1中的曲线代表利用UrQMD模型计算得到的理论结果,其中,实线为仅考虑自由的核子-核子弹性散射反应截面(σfree)的级联(Cascade)UrQMD模型的计算结果,短划线为加入形成和“预形成”粒子软平均场势(pf-part&f-B SM-EoS)和没有考虑核子-核子弹性散射反应截面介质修正的UrQMD模型的计算结果,点线为加入形成和“预形成”粒子软平均场势和考虑介质修正后的核子-核子弹性散射反应截面()的UrQMD模型的计算结果,模拟中运用了碎块形成判断条件dr<5.0 fm,dp<0.5 GeV/c,数据点是E895合作组[17]的实验结果.从图1可以看出:在UrQMD模型中加入形成和“预形成”粒子的平均场势后,中心快度区质子数偏高,但在[0.5,1]快度区内的自由质子分布趋势与实验结果相同;加入核子-核子弹性散射反应截面介质修正后,中心快度区质子数略有减少,且没有改变[0.5,1]快度区间的质子分布趋势.由此可知,利用UrQMD模型计算2A GeV核阻止效应时,形成和“预形成”粒子的平均场势与截面介质修正都应考虑.
图2所示为AGS能区实验入射粒子能量Elab为2A,4A,6A,8A和11A GeV Au+Au中心碰撞(σ/σT<5%)中自由质子的快度分布.图2(a)给出了无核子-核子弹性散射反应截面介质修正的级联模式UrQMD模型的计算结果,图2(b)给出了加入形成和“预形成”粒子的平均场势与截面介质修正后UrQMD模型的计算结果,模拟中运用了dr<5.0 fm,dp<0.5 GeV/c的碎块形成判断条件.图2中的数据点是E895合作组[17]和E802合作组[18]的实验结果.从图 2可以看出,利用UrQMD模型计算AGS能区核阻止效应时,考虑形成和“预形成”粒子的平均场势与截面介质修正后,给出的自由质子数分布趋势更接近实验结果,且在中心快度区得到的自由质子数随着入射能量的增加偏差程度进一步减小.
图3所示为AGS能区2A,4A,6A,8A和11A GeV Au+Au中心碰撞(σ/σT<5%)中自由质子的快度分布.图3中实线为加入形成和“预形成”粒子的平均场势与截面介质修正后UrQMD模型的计算结果,模拟时运用了碎块形成判断条件dr<5.0 fm,dp<0.5 GeV/c以及自由质子产额=αNfreep,同时给出了α的值;数据点是E895合作组[17]和E802合作组[18]的实验结果.从图3可以看出,UrQMD模型计算结果在AGS能区与实验数据符合得较好,且参数α的值随着入射能量的增加而增大.

图1 2A GeV的Au+Au中心碰撞(σ/σT<5%)中自由质子的快度分布

图2 AGS能区2A,4A,6A,8A和11A GeV Au+Au中心碰撞(σ/σT<5%)中自由质子的快度分布 (a)无核子-核子弹性散射反应截面介质修正的级联模式UrQMD模型的计算结果;(b)加入形成和“预形成”粒子的平均场势与截面介质修正后UrQMD模型的计算结果
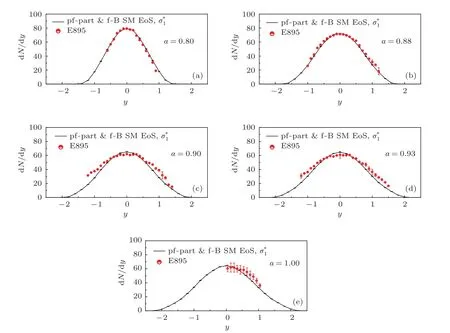
图3 AGS能区2A,4A,6A,8A和11A GeV Au+Au中心碰撞(σ/σT<5%)中自由质子的快度分布及相应的α值 (a)Elab=2A GeV;(b)Elab=4A GeV;(c)Elab=6A GeV;(d)Elab=8A GeV;(e)Elab=11A GeV
4 结论
本文运用修正的UrQMD模型研究了AGS能区Au+Au碰撞中的核阻止效应,该模型考虑了核子-核子弹性散射截面介质修正和新的碎块形成判断条件.模拟结果表明,考虑了平均场势、截面修正和碎块形成后的UrQMD模型能够很好地再现实验数据,但在高能区三者之间的关联及其内部机制还有待进一步研究.
[1]Alt C,Anticic T,Baatar B,Barna D,Bartke J,Betev L,Białkowska H,Blume C,Boimska B,Botje M,Bracinik J,Bramm R,Bunčić P,Cerny V,Christakoglou P,Chung P,Chvala O,Cramer J G,Csató P,Dinkelaker P,Eckardt V,Flierl D,Fodor Z,Foka P,Friese V,G´al J,Ga´zdzicki M,Genchev V,Głdysz E,Grebieszkow K,Hegyi S,Höhne C,Kadija K,Karev A,Kikola D,Kliemant M,Kniege S,Kolesnikov V I,Kornas E,Kowalski M,Kraus I,Kreps M,Laszlo A,Lacey R,van Leeuwen M,L´evai P,Litov L,Lungwitz B,Makariev M,Malakhov A I,Mateev M,Melkumov G L,Meurer C,Mischke A,Mitrovski M,Moln´ar J,Mrówczy´nski S T,Nicolic V,P´alla G,Panagiotou A D,Panayotov D,Petridis A,Peryt W,Pikna M,Pluta J,Prindle D,Pühlhofer F,Renfordt R,Richard A,Roland C,Roland G,Rybczy´nski M,Rybicki A,Sandoval A,Schmitz N,Schuster T,Seyboth P,Sikl´er F,Sitar B,Skrzypczak E,Slodkowski M,Stefanek G,Stock R,Strabel C,Ströbele H,Susa T,Szentp´etery I,Sziklai J,Szuba M,Szymanski P,Trubnikov V,Utvić M,Varga D,Vassiliou M,Veres G I,Vesztergombi G,Vranić D,Wetzler A,Włodarczyk Z,Wojtaszek A,Yoo I K,Zim´anyi J 2008 Phys.Rev.C 78034918
[2]Sun J X,Liu F H,Wang E Q 2010 Chin.Phys.Lett.27032503
[3]Wang E Q,Liu F H,Rahim M A,Fakhraddin S,Sun J X 2011 Chin.Phys.Lett.28082501
[4]Liu F H 2008 Chin.Phys.B 17883
[5]Anchishkin D,Muskeyev A,Yezhov S 2010 Phys. Rev. C 81031902(R)
[6]Abdel-Waged K,Felemban N,Uzhinskii V V 2011 Phys.Rev.C 84014905
[7]Reisdorf W,Andronic A,Gobbi A,Hartmann O N,Herrmann N,Hildenbrand K D,Kim Y J,Kirejczyk M,Koczo´n P,Kress T,Leifels Y,Schüttauf A,Tymi´nski Z,Xiao Z G,Alard J P,Barret V,Basrak Z,Bastid N,Benabderrahmane M L,Čaplar R,Crochet P,Dupieux P,Dželalija M,Fodor Z,Grishkin Y,Hong B,Kecskemeti J,Korolija M,Kotte R,Lebedev A,Lopez X,Merschmeyer M,Mösner J,Neubert W,Pelte D,Petrovici M,Rami F,deSchauenburg B,Seres Z,Sikora B,Sim K S,Simion V,Siwek-Wilczynska K,Smolyankin V,Stockmeier M,Stoicea G,Wagner P,Wiśniewski K,Wohlfarth D,Yushmanov I,Zhilin A 2004 Phys.Rev.Lett.92232301
[8]Bleicher M,Zabrodin E,Spieles C,Bass S A,Ernst C,Soff S,Bravina L,Belkacem M,Weber H,Stocker H,Greiner W 1999 J.Phys.G 251859
[9]Yuan Y 2010 Ph.D.Dissertation(Taiyuan:Shanxi University)(in Chinese)[袁颖2010博士学位论文(太原:山西大学)]
[10]Yuan Y,Li Q F,Li Z X,Liu F H 2010 Phys.Rev.C 81034913
[11]Zhang Y X,Li Z X,Danielewicz P 2007 Phys.Rev.C 75034615
[12]Danielewicz P,Barker B,Shi L 2009 AIP Conf.Proc.1128104
[13]Li Q F,Bleicher M 2009 J.Phys.G 36015111
[14]Li Q F,Bleicher M,Stocker H 2008 Phys.Lett.B 659525
[15]Klakow D,Welke G,Bauer W 1993 Phys.Rev.C 481982
[16]Zhang Y X,Li Z X,Zhou C S,Tsang M B 2012 Phys.Rev.C 85051602(R)
[17]Klay J L,Ajitanand N N,Alexander J M,Anderson M G,Best D,Brady F P,Case T,Caskey W,Cebra D,Chance J L,Chung P,Cole B,Crowe K,Das A C,Draper J E,Gilkes M L,Gushue S,Heffner M,Hirsch A S,Hjort E L,Huo L,Justice M,Kaplan M,Keane D,Kintner J C,Krofcheck D,Lacey R A,Lauret J,Law C,Lisa M A,Liu H,Liu Y M,McGrath R,Milosevich Z,Odyniec G,Olson D L,Panitkin S Y,Pinkenburg C,Porile N T,Rai G,Ritter H G,Romero J L,Scharenberg R,Schroeder L,Srivastava B,Stone N T B,Symons T J M,Wang S,Wells R,Whitfield J,Wienold T,Witt R,Wood L,Zhang W N 2002 Phys.Rev.Lett.88102301
[18]Akiba Y,Ahle L,Akiba Y,Ashktorab K,Baker M D,Beavis D,Britt H C,Chang J,Chasman C,Chen Z,Chi C Y,Chu Y Y,Cianciolo V,Cole B A,Crawford H J,Cumming J B,Debbe R,Dunlop J C,Eldredge W,Engelage J,Fung S Y,Garcia E,Gonin M,Gushue S,Hamagaki H,Hayano R S,Hayashi S,Heintzelman G,Homma S,Judd E,Kaneko H,Kang J,Kim E J,Kumagai A,Kurita K,Lee J H,Levine M J,Luke J,Miake Y,Mignerey A,Moskowitz B,Moulson M,Muentz C,Nagamiya S,Namboodiri M N,Ogilvie C,Olness J,Remsberg L P,Sako H,Sangster T C,Seto R,Shea J,Shigaki K,Soltz R,Steadman S G,Stephans G S F,Tannenbaum M J,Thomas J H,Videbæk F,Wang F,Wang Y,Wu Y,Xiang H,Xu G H,Yagi K,Yang X,Yao H,Zajc W A,Zhu Q,Zhu F 1996 Nucl.Phys.A 610139

