两类多项式微分系统的可积性问题

桑 波

(聊城大学 数学科学学院，聊城252059)

0 引言

在常微分方程定性理论中，焦点量与鞍点量是两类重要的奇点判定量．形式幂级数法作为计算这两类判定量的理论方法，在实际应用中效率普遍不高．刘一戎、陈海波［1］基于奇点量与焦点量、鞍点量的代数等价关系，给出了奇点量的线性递推公式，从而避免了复杂的非线性代数方程组的求解．王东明［2］在形式幂级数法的基础上，通过反复使用伪除法有效地提高了焦点量的计算效率．

考虑平面微分系统

对于系统(1)，总存在形式幂级数

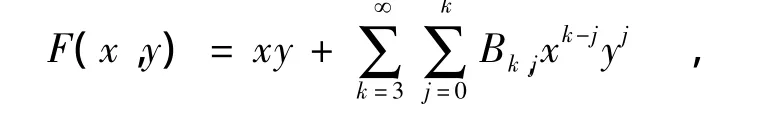
使得

其中Ws称为系统(1)在原点的第s阶奇点量．

设n为任意给定的自然数，对(2)式中间部分合并同类项得:

其中 Vn，fl，j，f2n+2，j都是关于诸参数 ak，j，bk，j和诸变量 Bk，j的多项式，且关于诸变量 Bk，j是线性的;h．o．t．表示2n+3次以上的项．

根据［7］的消元技巧，先指定诸变量 Bk，j的次序;再将诸 f2n+2，j，fl，j适当整序得到关于诸变量 Bk，j的三角列TSn;最后求多项式Vn+v关于三角列TSn的伪余式Rn，则第n阶奇点量Wn满足－v，其中coeff(Rn，v)表示多项式Rn关于v的一次项系数，v为临时引进的变量．由于奇点量序列W1，W2，…，Wn通常非常复杂，在具体应用时需要约化．即求诸 Wk(2 ≤k ≤n)相对于多项式组 W1，W2，…，Wk－1的 GrÖbner基［8－9］的余多项式 W1k，从而得到约化奇点量序列

考虑右端函数为n次多项式的二维微分自治系统

定义1［10］设f(x，y)是一个m次多项式，如果存在多项式h(x，y)，使得

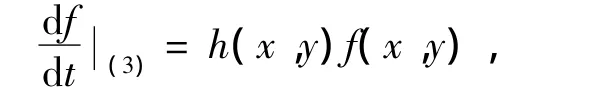
则称f=0是系统(3)的m次不变代数曲线，并称f是系统(3)的代数积分，h称为f的余因子．

注 由上面的定义，多项式f是系统(3)的代数积分的充要条件是在纯字典序plex(x，y)下，)关于f的余式R≡0．

引理1［10］设f1，f2，…，fm是系统(3)的m个独立的代数积分，满足

如果存在一组不全为零的复常数 α1，α2，…，αm，使得

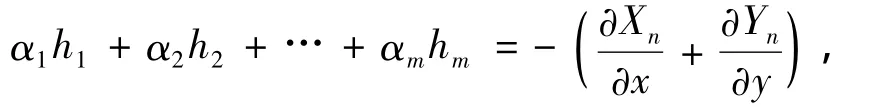
则 f=fα11fα22…fαmm是系统(3)的一个 Darboux 积分因子．

引理2［11］系统(1)在原点可积的充要条件是该系统具有形式首次积分

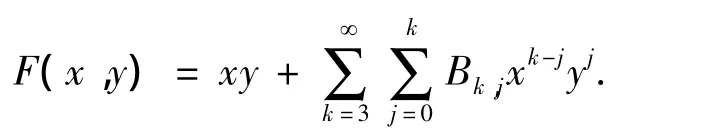
1 一类复三次系统的可积性条件

考虑一类复三次系统

利用引言给出的奇点量计算方法，求得系统(4)的前7阶约化奇点量:

定理1 系统(4)在原点可积的充要条件是下列6组条件之一成立:

(1)b1=b2=b4=b5=b6=0;

(2)b2=b4=b6=0，b3=

(3)b4=0，b1

(4)b1=b3=b4=b6=0，b5=

(5)b7=0，b6= －b2b3;

(6)b1=

证明 必要性首先计算系统(4)的前7阶奇点量的约化GrÖbner基G;然后对多项式组G进行零点分解，共得到6组独立的系数条件．

充分性 当条件(1)成立时，系统(4)变为:

当条件(2)成立时，系统(4)变为:

当条件(3)成立时，系统(4)变为:

系统(7)以μ3x，(y)=e为积分因子，因此系统(7)在原点可积．

当条件(4)成立时，系统(4)变为:

当条件(5)成立时，系统(4)变为:

假设系统(9)具有形如F(x，y)=∑∞n=1vn(y)xn的形式积分，则有递推公式

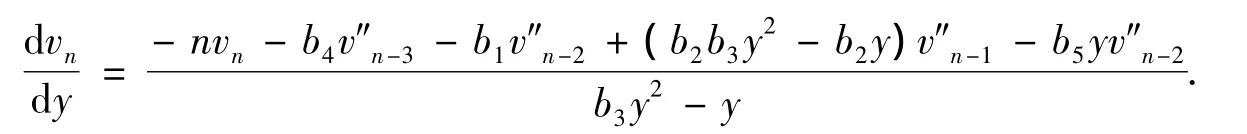
令v－2(y)=v－1(y)=v0(y)=0，通过逐项求解并适当选取积分常数，依次得到:

通过数学归纳法和递推公式，不难证明vn(y)可具有如下形式:

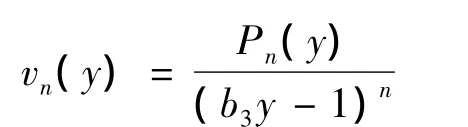
其中Pn(y)为次数为n的多项式．所以系统(9)具有形式首次积分，从而由引理2，系统(9)在原点可积．

当条件(6)成立时，系统(4)变为:

2 一类复四次系统的可积性条件

考虑一类复四次系统

利用引言给出的奇点量计算方法，求得系统(11)的前8阶约化奇点量:

定理2 系统(11)在原点可积的充要条件是下列两组条件之一成立:

(1)b7=0， b6=－b2b3;

(2)b1=b2=b3=b4=b5=b6=0．

证明 必要性 首先计算系统(11)的前8阶奇点量的约化GrÖbner基G;然后对多项式组G进行零点分解，共得到两组独立的系数条件．

充分性 当条件(1)成立时，系统(11)化为

假设系统(12)以 F(x，y)= ∑∞n=1vn(y)xn为形式首次积分，则有递推公式

令v－3(y)=v－2(y)=…=v0(y)=0，通过逐项求解并适当选取积分常数，依次得到:

其中

通过数学归纳法和递推公式，不难证明vn(y)可具有如下形式:

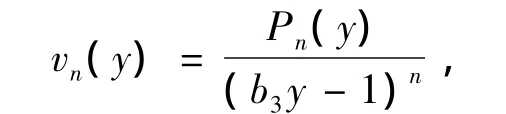
其中Pn(y)为次数为n的多项式．所以系统(12)具有形式首次积分，从而由引理2，系统(12)在原点可积．

当条件(2)成立时，系统(11)化为

假设系统(13)以 F(x，y)= ∑∞n=1v4n－3(y)x4n－3为形式首次积分，则有递推公式

令v－3(y)=0，通过逐项求解并适当选取积分常数，依次得到:

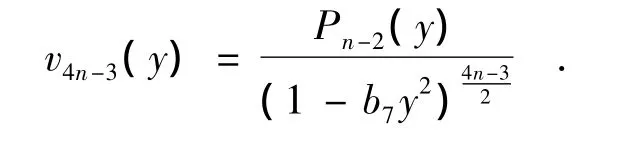
通过数学归纳法和递推公式，不难证明当n＞1时，v4n－3(y)可具有如下形式:其中Pn－2(y)为次数为n－2的多项式．所以系统(13)具有形式首次积分，从而由引理2，系统(13)在原点可积．

［1］CHEN H B，LIU Y R．Linear recursion formulas of quantities of singular point and applications［J］．Applied Mathematics and Computation，2004，148(1):163 －171．

［2］WANG D M．Mechanical manipulation for a class of differential systems［J］．Journal of symbolic computations，1991，12(2):233－254．

［3］刘一戎．一类三次系统的奇点量公式和可积性条件，M(3)≥7［J］．科学通报，1989，34(17):1299－1301．

［4］ROMANOVSKII V G，SHCHEGLOVA N L．The integrability conditions for two cubic vector fields［J］．Differential Equations，2000，36(1):108 －112．

［7］杨路，张景中，侯晓荣．非线性代数方程组与定理机器证明［M］．上海:上海科技教育出版社，1996．

［8］刘木兰．GrÖbner基理论及其应用［M］．北京:科学出版社，2000．

［9］桑波．两类三次微分系统的中心焦点问题［J］．南京师范大学学报:自然科学版，2012，35(2):16－21．

［10］刘一戎，李继彬．平面向量场的若干经典问题［M］．北京:科学出版社，2010．

［11］MATTEI JF，MOUSSU R．Holonomie et intégrates premières［J］．Ann Sci Ecole Normale Superieure，1980，13(4)，469－523．