基于盖根鲍尔多项式的SVM核函数

张瑞，杨晓，谭秀林

（山东理工大学 理学院，山东 淄博 255049）

核函数是支持向量机重要的组成部分，近些年在分类和回归等问题中得到了广泛的应用［1－10］，基于盖根鲍尔多项式，我们提出了盖根鲍尔核函数.通过对盖根鲍尔核函数性态研究以及在双螺旋集和标准的UCI数据集上的实验，表明盖根鲍尔核函数比常用的核具有更强的鲁棒性，并且在泛化性能上有更好或相当的表现.

1 核函数及性质

定义1 （核函数）设Χ是Rn的一个子集，称定义在Χ×Χ上的函数是核函数，如果存在着从Χ到某个Hilbert空间 H 的映射Φ，使得Κ（x，z）＝〈Φ（x），Φ（z）〉.（其中〈，〉表示内积）.

定理1 设K1（x，z）与K2（x，z）是X×X 上的核函数，则

（1）K（x，z）＝K1（x，z）＋K2（x，z） （2）K（x，z）＝K1（x，z）×K2（x，z）均是X×X上的核函数.

2 盖根鲍尔核函数

先介绍盖根鲍尔多项式：

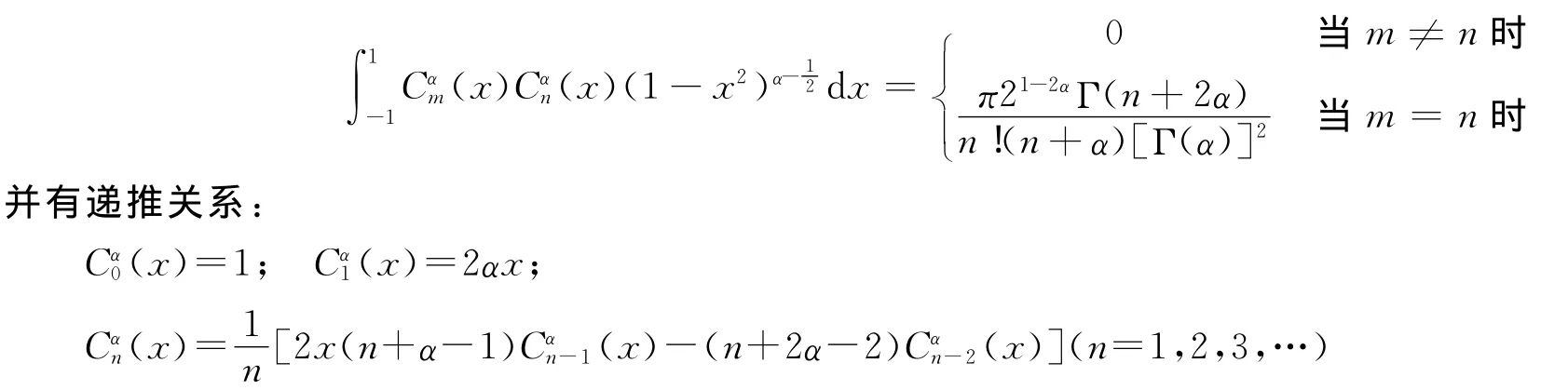
先把盖根鲍尔多项式推广成广义的盖根鲍尔多项式：

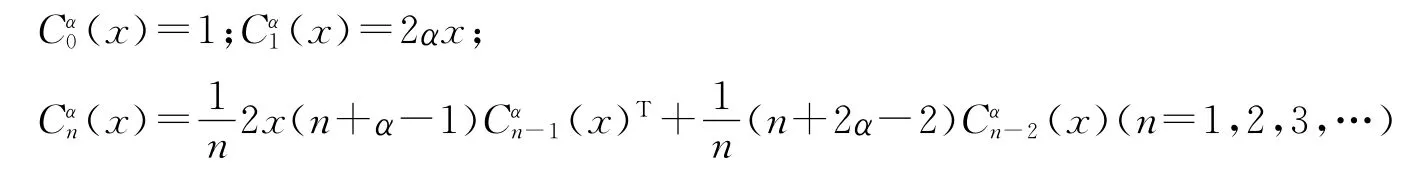
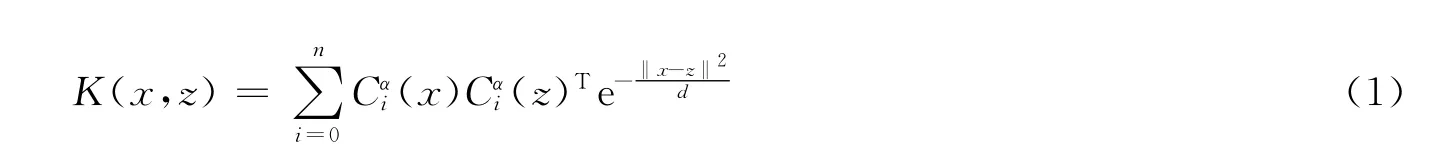
其中d表示向量x与z的维数，下面证明（1）式定义的函数为函数.

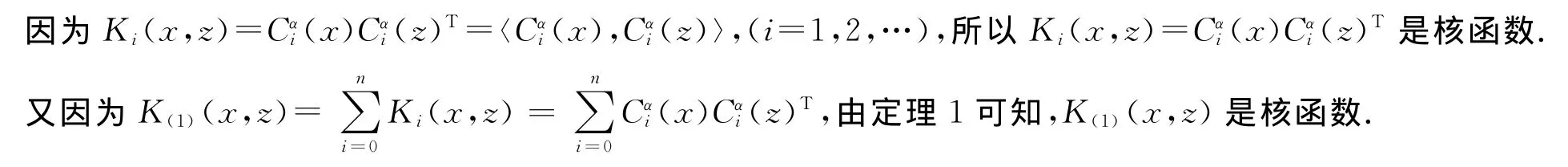
表1 0阶到2阶的盖根鲍尔核函数Table 1 List of the Gegenbauer kernel function up to second order

3阶的盖根鲍尔核函数为：

图1－图2分别显示了0阶到3阶的盖根鲍尔核函数在x⊆［－4，－4］，z＝－0.8，0以及α＝1.0，0.5对应的图形.

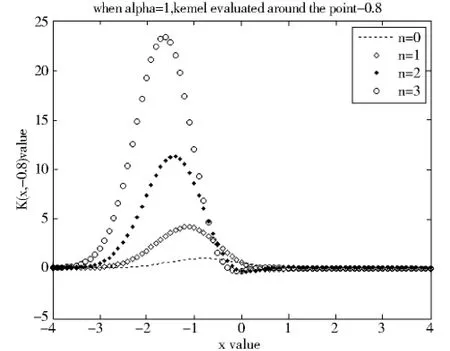
图1 盖根鲍尔核函数在z＝－0.8，α＝1.0对应的图形Fig.1 Figures of Gegenbauer kernel when z＝－0.8，α＝1.0

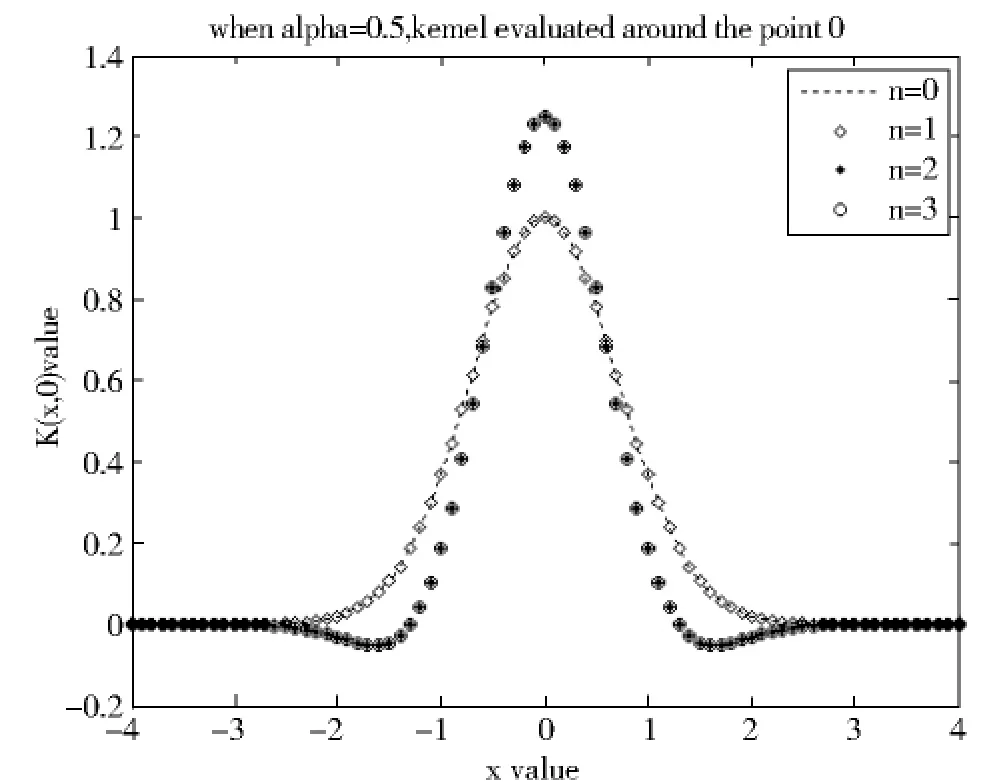
图2 盖根鲍尔核函数在z＝0，α＝0.5对应的图形Fig.2 Figures of Gegenbauer kernel when z＝0，α＝0.5

3 实验结果与分析

3.1 在双螺旋集上的分类对比

实验中我们对有噪声与无噪声的双螺旋集分别进行了实验（图3、图4，P32）.

由于多项式核不能将双螺旋集正确分类［9－10］，所以我们在该实验中选择了高斯核与盖根鲍尔核做对比实验.表2列出了该试验中核函数参数的取值.表3和表4显示了核函数能将双螺旋集正确分类相对应的最大间隔和支持向量个数.

表2 实验中所用的核函数及参数的取值Table 2 Kernels and their parameter values used in the experiments

表3 在无噪声下条件最大间距，支持向量的个数Table 3 The Number of maximum margin and support vectors on the no－noise bi－spiral problem

表4 有噪声条件下最大间隔，支持向量个数Table 4 The Number of maximum margin and support vectors on the noisy bi－spiral problem

由表3和表4可以看出，盖根鲍尔核对应的间隔最大，而支持向量个数最少.

图3 2阶盖根鲍尔核函数在无噪声双螺旋集上的分类边界Fig.3 Boundary with 2order Gegenbauer kernel on no－noise bi－spiral data

图4 2阶盖根鲍尔核函数在有噪声双螺旋集上的分类边界Fig.4 Boundary with 2order Gegenbauer kernel on noisy bi－spiral data

3.2 在标准UCI数据集上的分类对比

该实验中，我们在标准的UCI数据集上做分类对比实验，用到的数据集见表5.盖根鲍尔核与高斯核的参数取值见表5，多项式核参数n取值从自然数1到5.实验结果列在表6（P33）.

表5 实验中的核函数在标准UCI数据集Table 5 UCI benchmark data sets used in the experiments

表6 实验中的函数在标准UCI数据集对应的最大精度Table 6 Maximum accuracy on the UCI benchmark data sets

由表6可以看出，在banana与breast－cancer数据集上，盖根鲍尔核函数与高斯核、多项式核相当，在其它的数据集，盖根鲍尔核比高斯核与多项式核具有更好的表现.

4 结论与展望

本文基于盖根鲍尔多项式，提出了盖根鲍尔核函数，在双螺旋集及UCI数据集上与常用的核函数（多项式核，高斯核）做了分类实验对比.实验表明，盖根鲍尔核函数与最常用核函数（高斯核与多项式核）进行对比，具有更好的鲁棒性，有更好或相当的泛化性能.由此可看出，本文提出的盖根鲍尔核函数可以作为一般的核函数，取代上述常用的核函数.

［1］Vapnik V.Statictical Learning Theory［M］.New York：Wiley，1998.

［2］Artan Y，Huang X.Combining Multiple 2nu－SVM Classifiers for Tissue Segmentation［C］／／IEEE ISBI，2008：488－491.

［3］Chen C H，Ho P G P.Statistical Pattern Recognition in Remote Sensing［J］.Pattern Recognition41，2008，9：2731－2741.

［4］Wu Z L，Li C H，Ng J K Y，et al.Location Estimation Via Support Vector Regression［J］.IEEE Trans Mobile Comput，2007，6（3）：311－321.

［5］Zhang R，Wang W J.Facilitating the Applications of Support machine by Using a new kernel［J］.Expert Systems with Application，2011，38：14225－14230.

［6］Zhang R，Wang W J.Learning Linear and Nonlinear PCA with Linear programming［J］.Neural Processing Letters，2011，33：151－170.

［7］Zhang R，Wang W J.Approximations of the Standard Principal Components Analysis and Kernel PCA［J］.Expert Systems with Applications，2010，37（9）：6531－6537.

［8］Zhang R，Wang W J，Ma Y C.Least Square Transduction Support Vector Machine［J］.Neural Processing Letters，2009，29（2）：133－142.

［9］张瑞，高红，张立伟.一类新的支撑向量机核函数－埃尔半特核函数［J］.山西大学学报：自然科学版，2012，35（1）：38－42.

［10］张瑞，王文剑，张亚丹，等.基于支持向量机分类问题的勤让德核函数［J］.计算机科学，2010，39（7）：222－224.