非负矩阵分解在能力验证中的应用

李顺勇，易利红，陈勇，张晓琴

（1.山西大学 计算机与信息技术学院，山西 太原 030006；2.山西大学 数学科学学院，山西 太原 030006；3.山西出入境检验检疫局检验检疫技术中心，山西 太原 030024）

0 引言

能力验证（Proficiency Testing）是指利用实验室间比对来判定实验室和检查机构能力的活动，也是认可机构加入和维持国际相互承认协议（MRA）的必要条件之一.实验室能力验证，是指利用实验室间指定检测数据的比对［1］，确定实验室从事特定测试活动的技术能力.目前我国已经大量地开展了能力验证活动，这些能力验证计划为我国各级部门或机构用于对实验室测试能力和测试水平的监督、考评，同时也是实验室自身质量控制的一种有效的、客观的手段.能力验证计划的开展和利用，为我们国家实验室的计量认证、认可提供了有力的技术支持［2］.

目前，我国检测领域的能力验证活动，在对结果的统计分析中大多数使用稳健统计方法，即Z比分数的方法［3］.此方法的优点是计算简单、容易掌握，但在实际使用过程中出现了一些问题.比如：Z比分数的判定结果与相应的检测标准的判定结果有冲突进行描述；常量分析、微量分析的适用性；提供信息少，缺乏深入细致的描述，无法对实验室数据之间的相关性进行描述，且只能对单个项目分析，缺乏整体性，无法解决由比对内容与对象不断增加而带来的问题.另外一个突出的问题是，在用稳健的统计分析方法进行分析结果时，往往假定数据是服从正态分布的，但是通过对大量实际数据的分析发现，有相当一部分数据不满足正态分布的假设.这样利用稳健统计得出的Z比分数判定结果与测试标准规定的判定结果冲突，造成了对参加的实验室无从分析，测试结果是否准确及可靠无从判定，从而有些实验室对能力验证的结果产生了质疑，同时造成能力验证实施机构不能正确运用相应的统计方法对结果进行判定.因此寻找更加有效的统计方法就变得极为重要.

基于以上对能力验证的认识，结合统计学中相关方法的研究，我们发现，在不考虑实验数据的分布类型时，能力验证在某种意义上是一种分类问题.因此可以考虑将一些统计上比较成熟的分类方法，如非负矩阵分解方法用于能力验证问题的研究中.本文尝试将非负矩阵分解方法应用于能力验证数据的统计分析中，同时结合稳健统计方法，来获得更加全面的信息.此种算法目前已被应用到诸多领域，如图像分析、语音处理、机器人控制、生物医学工程和化学工程、文本聚类及数据挖掘等，本文主要研究非负矩阵分解在能力验证中的应用.

1 非负矩阵分解（Non－negative Matrix Factorization，NMF）

1.1 原理［4－8］

考虑如下的基本线性统计模型：Vn×m＝Wn×rHr×m＋En×m，这里Vn×m表示一个非负观测数据矩阵；Wn×r和Hr×m是因子矩阵；En×m是误差矩阵.当不考虑误差时，该式可简写为下式：

式（1）表示任一非负数据矩阵可分解为两个非负矩阵的乘积.其中n是变量数，m是样本（或变量）数，r表体系的主成分个数.且因子矩阵W的列数要远少于矩阵V的行数，即它可以通过少数几个变量来表征原始数据V.

一般采用矩阵之间的欧氏距离作为衡量和评价原始数据V与分解后的WH（WH＝W×H）接近程度的指标.且V和WH之间的欧氏距离平方定义如下：

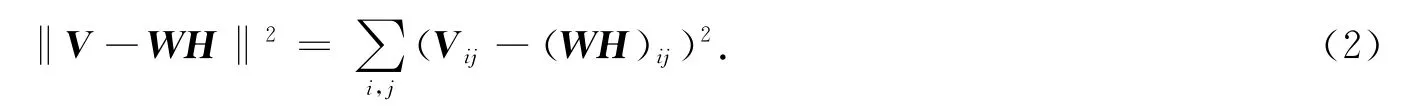
当且仅当V＝WH时，上式值为零.本文采用欧氏距离的平方构建评价函数F：

1.2 基本算法

NMF算法的步骤如下：

（i）对所求非负矩阵W和H随机地赋初值；

（ii）由H计算W：

（iii）对W 进行列归一化：

（iv）借助上一步计算出的W 计算新的H：

（v）重复步骤（ii）－（iv）直至收敛.

当迭代达到（3）式中的F小于给定临界值时，迭代终止.最后求得的W和H即为所求的非负因子矩阵.

2 数值实验

2.1 实验数据

为验证NMF算法在能力验证数据处理中的适用性，我们采用了CNAL T162水中微量挥发性卤代烃检测及CNAS T0387煤炭分析中的数据来说明问题.

2.2 数据预处理

CNAL T162水中微量挥发性卤代烃检测能力验证计划共有79个实验室报名参加、73个实验室在规定的时间内报告了检测结果，这些实验室主要来自环境保护、卫生防疫和城市供水系统，分别占参加实验室总数的48.6%、26.4%和19.4%.为了保护参加实验室的权益，对正式报名参加的每一个实验室均赋予一个代码，代码号为1－79.个别实验室因技术条件限制，最终未能报告检测结果，其代码将不会在报告中出现.

CNAS T0387煤炭分析能力验证共邀请到91个实验室参加，涉及检验检疫、质检、环保、检验、公司、煤炭生产、运销和使用单位，分布在全国21个省、自治区和直辖市，为确保实验室的保密性，所有参加实验室均有一个唯一代码，代码号为1－91.个别实验室因技术条件限制，最终未能报告检测结果，其代码将不会在报告中出现.

为了方便用非负矩阵分解算法处理数据，对未出现报告检测结果的实验室代码均使用其对应的样品A和样品B由其他实验室所测得得到的中位值补齐.选用MATLAB软件进行数据处理

2.3 数据分析

实例一：CNAL T162水中微量挥发性卤代烃检测.

将样品A和样品B看成两类，编号1－79为一类，编号80－158为另外一类，即矩阵的行，将实验室检测4种挥发性卤代烃，即三氯甲烷、四氯化碳、三氯乙烯和四氯乙烯看成四个变量即矩阵的列，故得到158×4矩阵.

用MATLAB编程非负矩阵分解算法对数据进行分类后绘制的图形如图1所示，通过图1我们知道样品A和样品B中存在的离群实验室代码，见表1.

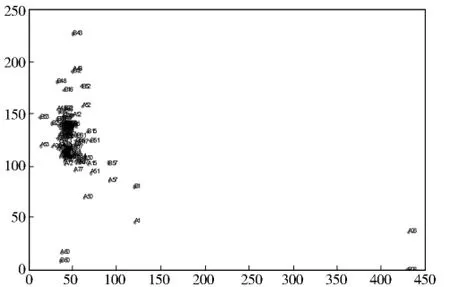
图1 水中微量挥发性卤代烃对样品A和样品B分类结果Fig.1 Trace volatile halogenated hydrocarbons in the classification results of sample Aand B

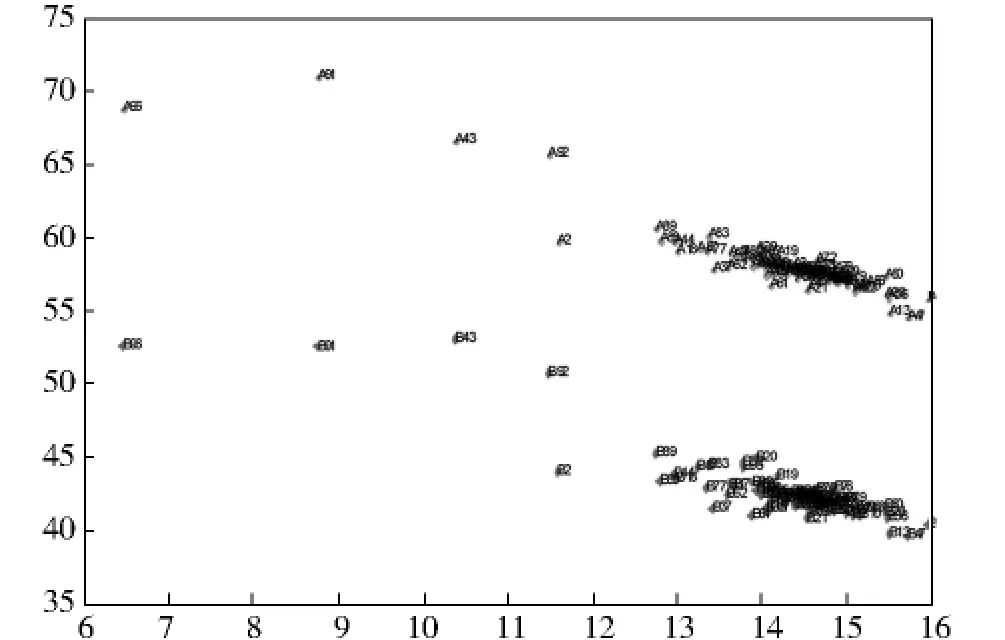
图2 煤炭分析对样品A和样品B分类结果Fig.2 Classification results of sample Aand Bof coal analysis

表1 水中微量挥发性卤代烃检测的不合格实验室代码及与Z比分数分析结果的比较Table 1 Disqualification laboratory code of trace volatile halogenated hydrocarbons testing compare NMF with the Z－score analysis

通过比对判别的不合格实验室代码结果可知，使用稳健统计方法即Z比分数［9］方法得到的结果比使用NMF多出一个实验室，代码为33，即四氯乙烯的检测结果实验室内ZW分数＝3.79，我们知道Z比分数判别不合格实验室的方法是：根据实验室间ZB分数或实验室内ZW分数绝对值大于等于3时认为是离群值，由此来说明该实验室目前的检测能力状况不满意.

实例二：CNAS T0387煤炭分析.

将样品A和样品B看成两类，编号1－91为一类，编号92－182为另外一类，即矩阵的行，将实验室检测煤炭中的灰分、挥发分、全硫、发热量4种成分看成四个变量，即矩阵的列，故得到182×4矩阵.用MATLAB编程非负矩阵分解算法对数据进行分类后绘制的图形如图2所示，通过图2我们知道样品A和样品B中存在的离群实验室代码，见表2（P28）.

表2 煤炭分析的不合格实验室代码及与Z比分数分析结果的比较Table 2 Disqualification laboratory code of coal analysis compare NMF with the Z－score

通过比对判别的不合格实验室代码结果可知，使用稳健统计方法即Z比分数方法得到的结果比使用NMF多出五个实验室，代码分别为9，35，52，62，86，我们知道代码为9号实验室是高位发热量测试结果实验室间ZB分数＝－3.44；代码为35号实验室是高位发热量测试结果实验室内ZW分数＝－3.18；代码为52号实验室是高位发热量测试结果实验室间ZB分数＝3.39；代码为62号实验室是全硫测试结果实验室间ZB分数＝3.07；代码为86号实验室是灰分测试结果实验室间ZB分数＝3.00；而Z比分数判别不合格实验室的方法是根据实验室间ZB分数或实验室内ZW分数绝对值大于等于3时认为是离群值，由此说明实验室目前的检测能力状况不满意.

3 结果分析与小结

3.1 结果分析

当参加实验室较多时，计算出的标准差可能偏小，易导致部分实验室的Z比分数大于3进而被误判为不满意.从表1及表2中非负矩阵分解结果可见，稳健统计方法与非负矩阵分解方法相结合可以对实验室的测试结果更好地进行判断，特别对于实验室测定结果处在临界值附近时有效.

3.2 小结

（1）稳健统计方法和NMF均可对能力验证的数据（包括非正态数据）进行统计分析，进而找出离群值.

（2）对于用稳健统计方法判断处于临界值附近的实验室，可以借助于NMF分析，对其归属提供参考.这说明两种方法可互为补充.

（3）NFM方法克服了稳健统计分析中只能逐一进行分析的缺撼.

（4）NFM方法在能力验证中的应用尚不完善，仍需更进一步的探讨.

［1］符颖操，罗茜.实验室间比对结果分析统计方法的探讨［J］.理化检验：物理分册，2006，42（6）：295－299.

［2］张元福，张壮耘，张雪茜，等.分析实验室能力验证数据统计评价方法研究［J］.现代测量与实验室管理，2003，11：45－48.

［3］徐建平，刁凤鸣.Z比分数在实验室能力验证检测中的运用［J］.江苏：环境监测管理与技术，2003，15（1）：42－43.

［4］徐森，卢志茂，顾国昌.结合K均值和非负矩阵分解集成文本聚类算法［J］.吉林大学学报：工学版，2011，41（4）：1077－1082.

［5］刘广军，高洪涛，刘建勇.非负矩阵因子分解用于中药 GC／MS重叠峰解析［J］.曲阜师范大学学报，2007，33（4）：83－86.

［6］高洪涛，李通化.非负矩阵因子分解算法理论和应用研究［D］.上海：同济大学，2005.

［7］Richard A Johnson，Dean W Wichem，陆璇.实用多元统计分析［M］.北京：清华大学出版社，2008.

［8］蒋淑敏，宋瑞，高洪涛，等.非负矩阵因子分解算法解析手性药物重叠峰的HPLC－DAD数据［J］.中国药科大学分析测试中心，2006，37（5）：432－437.

［9］李海峰，史乃捷，王军，等.聚类分析与稳健统计方法对CNAS T0402数据处理的比较和分析［J］.现代农业科技，2009（6）：258－263.