迭代容积粒子滤波算法在SINS初始对准中的应用*

迟凤阳，孙 枫，徐 博

（哈尔滨工程大学自动化学院，黑龙江哈尔滨 150001）

0 引言

在捷联惯性导航系统（SINS）中，初始对准是一项关键技术。对准精度与对准时间是影响整个系统性能的2个重要指标，而滤波技术在初始对准中具有极其重要的作用［1］。在初始失准角较小的情况下，SINS的误差模型可以简化为线性模型，一般用卡尔曼（Kalman）滤波方法进行处理;当初始失准角较大时，SINS的误差模型呈现非线性，需要采用非线性滤波技术进行处理［2］。

扩展卡尔曼滤波［3，4］（EKF）是目前常用的一种非线性滤波方法，EKF虽然简单而且容易实现，但它只是将非线性系统进行一阶线性近似，并且需要计算雅克比行列式，增加了算法的计算量，影响状态的估计精度。Julier S等人提出了基于 UT 变换的无迹卡尔曼滤波［5，6］（UKF）算法，UKF 直接利用非线性模型，使用UT变换得到一组sigma采样点来实现对状态向量后验分布的近似，避免了线性化误差，使得状态均值和方差的估计精度提高到二阶矩。UKF的精度虽然有所提高，但是随着系统维数的增大，不但计算量迅速增加，而且滤波性能急剧下降，甚至会导致发散。Arasaratnam Ienkaran等人提出了基于Cubature变换的容积卡尔曼滤波［7］（CKF）算法，CKF利用球形积分准则优化了UKF中的sigma点的采样方法和权重分配。在高维数系统中，CKF的滤波精度要高于UKF。针对于非线性、非高斯状态系统，文献［8，9］中提出了基于序贯蒙特—卡罗方法的粒子滤波（PF）算法，PF无需对状态模型进行线性化和高斯假设，可以处理任意非线性、非高斯系统中的状态估计问题。但是PF的缺点是重要性密度函数难以选取，且容易出现粒子退化问题［10，11］。

本文将 CKF 和 Gauss-Newton 迭代方法［12，13］相结合，得到迭代CKF（iterated CKF，ICKF）算法。利用ICKF算法获得PF算法的重要性密度函数，从而提出一种新的迭代容积PF（ICPF）算法，有效地解决了粒子退化问题。仿真结果和实验结果表明:将ICPF算法应用到SINS大失准角初始对准的过程中，有效地提高了对准的精度。

1 SINS静基座大方位失准角误差模型的建立

SINS初始对准是建立姿态矩阵初始值的过程。由于粗对准后的水平失准角很小，而方位失准角比较大，在这种情况下从当地地理坐标系（t系）到计算地理坐标系（t'系）之间的转换矩阵为

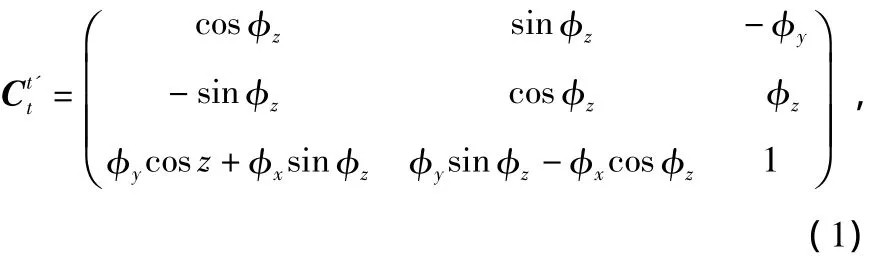
式中 φx，φy，φz分别为东向、北向和方位失准角。

SINS的速度误差和失准角模型如下［14，15］

式中 δv=［δvxδvyδvz］T为速度误差矢量，φ=［φxφyφz］T为失准角矢量为载体系到地理系的方向余弦矩阵为载体系到计算地理系的方向余弦矩阵为加速度计真实的比力输出，δfb为加速度计的测量误差，包括常值零偏和零均值高斯白噪声为陀螺的测量误差，包括常值漂移εb和零均值高斯白噪声为地球自转角速率在计算地理系的投影为地理系相对于地球系的转动角速率在计算地理系的投影为地理系相对于惯性系的转动角速率在计算地理系上的投影分别为的计算误差，δg为重力加速度的计算误差，可以忽略。

在静基座的条件下有v=0，略去垂直通道速度，将式（2）和式（3）展开，得到初始对准非线性模型的状态方程

式中Rm为子午面内的曲率半径，Rn为与子午面垂直的法线平面的曲率半径，φ为当地的纬度

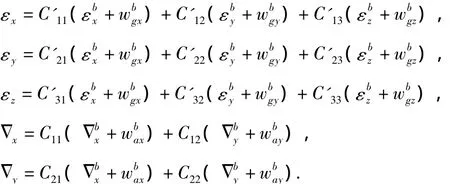
其中，Cij（i=1，2，3;j=1，2，3）为矩阵的第i行、第j列元素，C'ij（i=1，2，3;j=1，2，3）为的第i行、第j列元素。

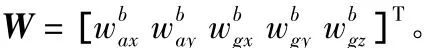
建立SINS的状态空间模型

式中f（X）和G的具体表达式参考表达式（4），H=［I2×202×3］，V为零均值高斯分布的观测噪声。

2 CKF算法

由贝叶斯估计原理可知，基于高斯假设的贝叶斯滤波估计算法的核心在于求解具有“非线性函数×高斯密度”形式被积函数的加权积分。考虑如下形式的多维积分

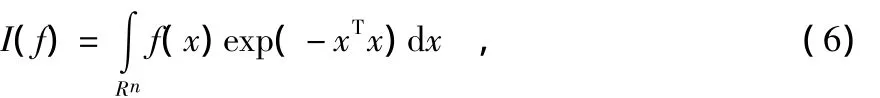
式中f（x）为任意函数，Rn为积分区域，上式的积分的解析解一般无法直接得到，因此，需要用近似的方法获得。

文献［7］指出采用 Spherical-Radial容积准则计算积分式（6）

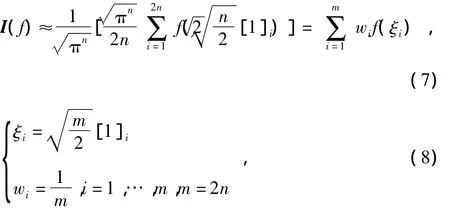
式中 ［1］i表示集合［1］的第i列，［1］为完整全对称点集，表示n维单位向量e=［1 0…0］T的元素进行全排列和改变元素符号所产生的点集;ξi为容积点，wi（i=1，2，…，m）为相应的权值，对于系统状态方程为三维的情况，即n=3 时有:［1］={（1，0，0）T，（0，1，0）T，（0，0，1）T，（－ 1，0，0）T，（0，－1，0）T，（0，0，－1）T}。

3 ICPF算法

式中C为常数。

定义代价函数为

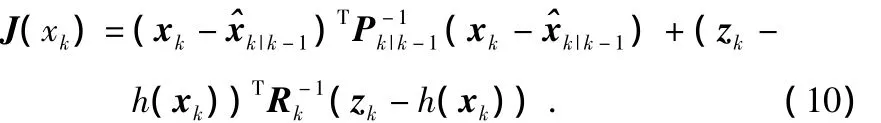
上式中的最大似然估计等价于求代价函数的最小值。利用Gauss-Newton迭代方法求解J（xk）最小值的第j+1次迭代公式为

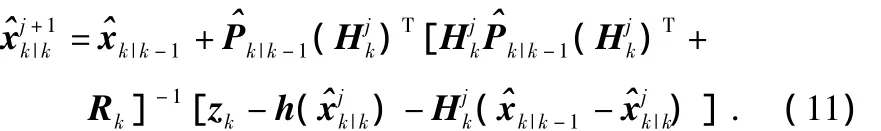
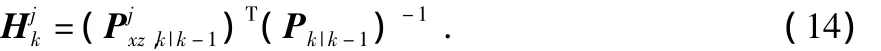
代入式（11）即可计算迭代更新。

由于标准PF采用状态转移先验概率密度作为建议分布，没有考虑最新量测值而完全依赖于模型，所以，导致滤波精度下降。本文利用ICKF算法获得PF算法的重要性密度函数，在时刻利用最新量测数据，产生新的后验概率密度分布，同时通过新的后验概率分布重新产生新的粒子，计算粒子的权值并归一化，最后进行重采样完成状态估计。ICPF算法流程如下:

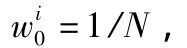
状态变量初值

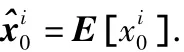
协方差阵初值

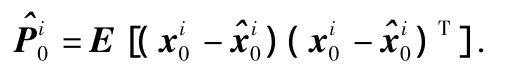
2）预测:k≥1，进行重要性采样，利用ICKF对每个粒子进行更新。

数字出版产业目前仍然存在着一些问题，例如，数字出版物的模式单一、盈利相对较少，品牌建设力量不足，数字出版物的侵权问题等。

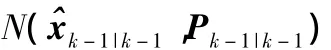
计算容积点 ξi（i=1，2，…，m）

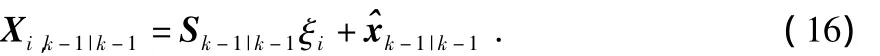
通过状态方程传播容积点

k时刻的状态预测值

k时刻的状态误差协方差预测值

再次进行Cholesky分解并计算容积点

通过量测方程传播容积点

k时刻的量测预测值

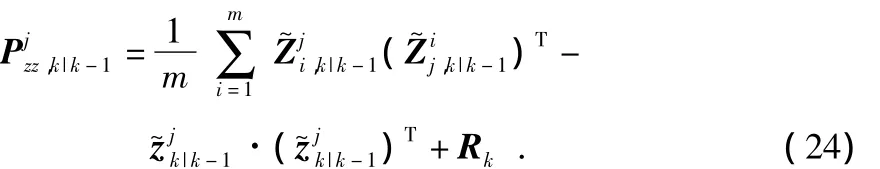
k时刻的估计互相关协方差阵

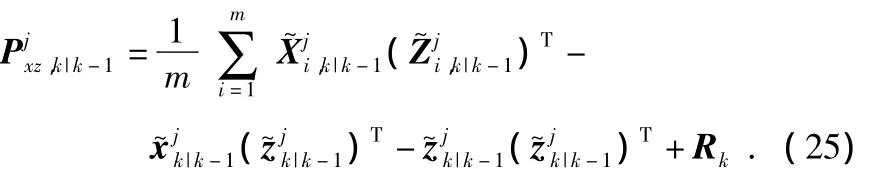
估计卡尔曼增益

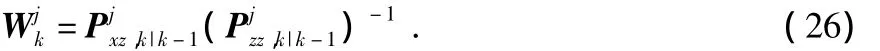
第j+1次迭代的状态和方差估计

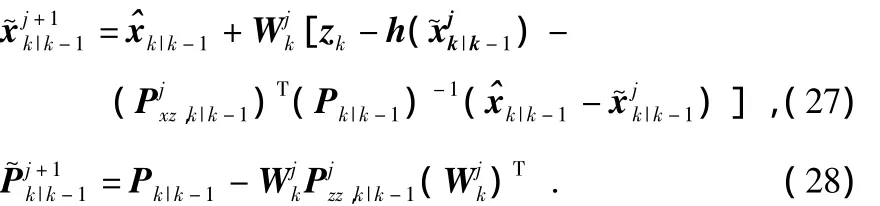
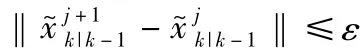
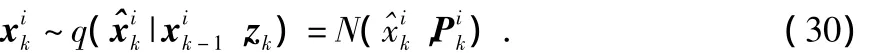
计算粒子权值并归一化

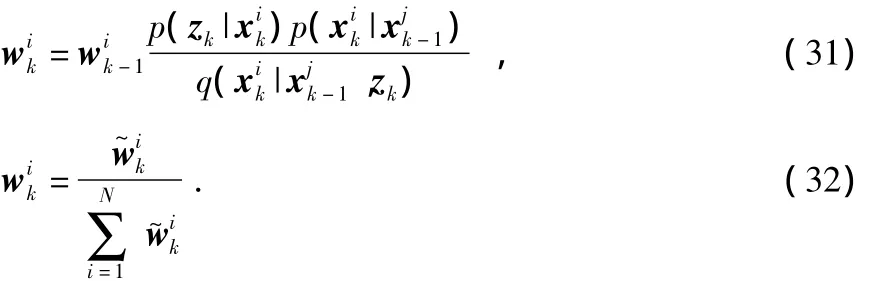
4）重采样:计算有效粒子数

设定门限值Nthreshold，若Neff＜Nthreshold，则认为粒子出现退化现象需要进行重采样;否则，不进行重采样。

5）状态估计与方差估计

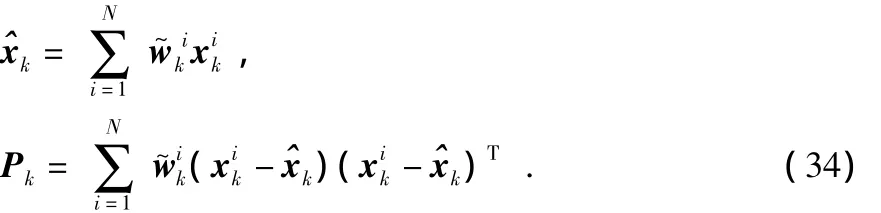
6）令k=k+1，返回步骤（2）直至滤波结束。

4 仿真分析

计算机仿真参数如下:系统状态初始值^x0为零，初始失准角 φx=φy=1°，φ2=10°，陀螺常值漂移为 0．01°/h，随机漂移0．005°/h，加速度计的零偏为 1 ×10－5gn，随机零偏为0．5 ×10－5gn，速度测量误差为 0．1 m/s，SINS 的初始位置为经度为 126．67°，纬度为 45．78°，高度为 0 m。针对上述条件分别利用PF，CPF，ICPF算法对SINS进行静基座初始对准仿真，粒子数N=1000，仿真时间t=300 s，仿真结果如图1～图3所示，各种滤波算法的估计误差如表1所示。

图1 横摇失准角估计误差Fig 1 Estimation error of rolling misalignment angle

从图1～图3和表1中能够看出:PF，CPF与ICPF算法对于横摇失准角和纵摇失准角的滤波估计精度和收敛速度比较理想，失准角稳态误差很小;而对大方位失准角的估计，ICPF在收敛速度和估计精度上，要优于PF和CPF算法。主要原因是标准的PF算法是以状态转移先验概率密度作为建议分布，容易出现粒子退化问题，而ICPF算法在迭代过程中利用最新量测信息改进迭代过程产生的新息方差和协方差，提高了滤波的收敛速度和数值稳定性。

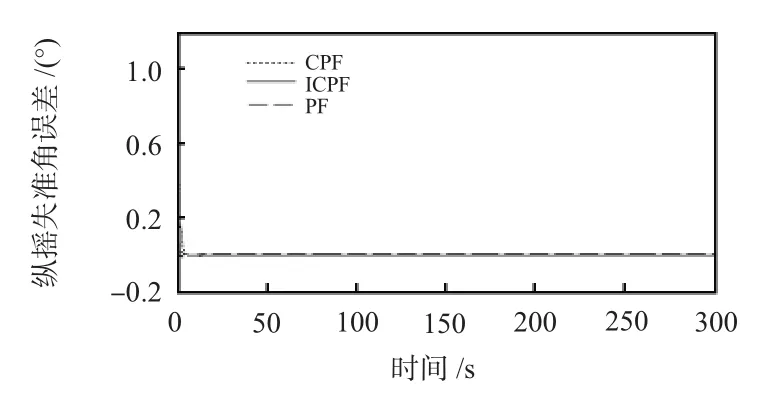
图2 纵摇失准角估计误差Fig 2 Estimation error of pitching misalignment angle

图3 航向失准角估计误差Fig 3 Estimation error of heading misalignment angle

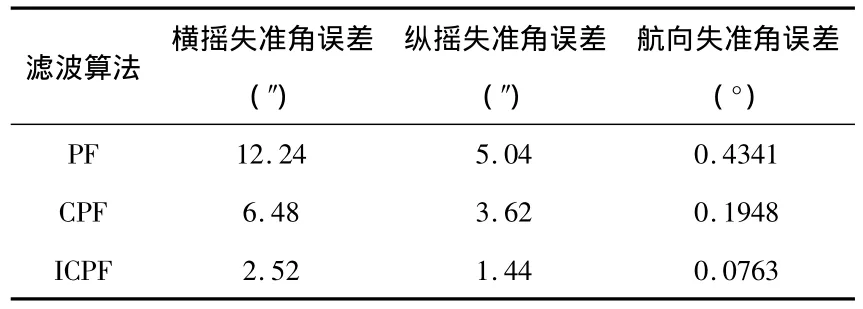
表1 PF，CPF与ICPF的估计误差Tab 1 Estimation error of PF，CPF与 ICPF

5 试验验证

教研室自行研制的光纤陀螺是目前国内光学陀螺中比较先进的一种，具有较好的精度和稳定性。试验中采用由3只光纤陀螺与3只石英加速度计及相应的信号处理电路组成的惯性测量单元（IMU）（见图4（a）），在SGT—3型惯导测试转台（见图4（b））上进行静基座对准的试验。

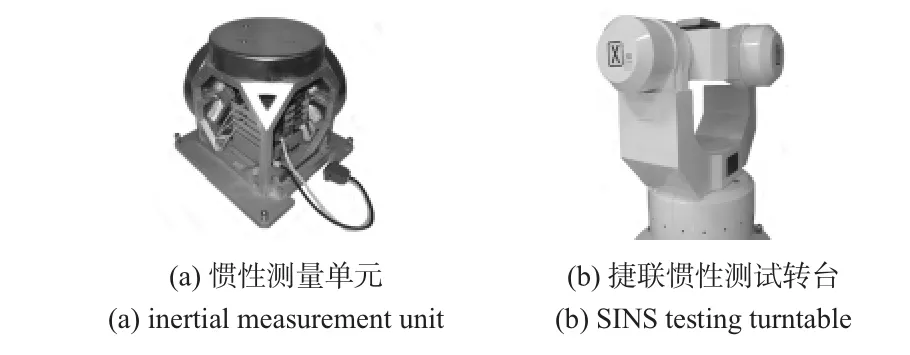
图4 惯性测量单元与捷联惯导测试平台Fig 4 Inertial measurement unit and SINS testing turntable

实验室转台的位置是北纬 45．7796°，东经 126．6705°。为了比较在相同数据源下CPF和ICPF的滤波性能，采用现场数据采集与离线计算分析的方法。试验中的测试数据经过了系统标定和系统误差补偿。考虑对准时间较短，认为陀螺的测量误差是由常值漂移与白噪声构成，加速度计测量误差由零偏与白噪声组成。3个初始失准角分别为φx=φy=1°，φz=10°。图5给出了航向失准角误差试验曲线图，表2给出了10次航向失准角估计误差平均值。

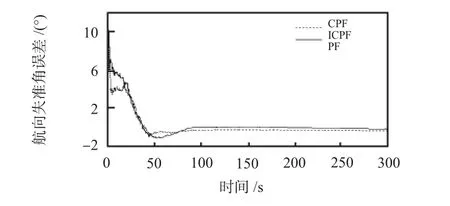
图5 航向失准角估计误差Fig 5 Estimation error of heading misalignment angle

表2 CPF与ICPF的航向失准角估计误差Tab 2 Estimation error of heading misalignment angle of CPF and ICPF

从试验结果可以看出:相对于CPF，ICPF更利于提高初始对准精度，从而在SINS静基座方位大失准角初始对准中应当选择ICPF作为滤波方法，这与仿真结论相一致。

6 结论

本文深入地研究了ICPF算法，并将其应用到SINS大方位失准角初始对准过程中。该算法使用容积数值积分方法直接计算非线性随机变量的均值和方差，使用Gauss-Newton迭代方法充分利用最新量测信息改进了迭代过程产生的新息方差和协方差，提高了状态估计精度。ICPF算法利用ICKF得到PF的重要性密度函数，有效地缓解了粒子退化问题。仿真结果和试验验证结果表明:ICPF算法在SINS大方位失准角初始对准中的可行性和优越性，是一种有效的非线性滤波算法。

［1］ 严恭敏，严卫生，徐德民．基于UKF滤波在SINS大失准角初始对准中的应用［J］．中国惯性技术学报，2008，16（3）:254－264．

［2］ Dmitriyev S P，Stepanov O A，Shepel S V．Nonlinear filtering methods application in INS alignment［J］．IEEE Trans on Aerospace and Electronic Systems，1997，33（1）:260 －271．

［3］ Athans M，Wishner R P，Bertolini A．Suboptimal state estimation for continuous time nonlinear systems from discrete noisy measurements［J］．IEEE Transactions on Automatic Control，1968，13:504－514．

［4］ ，Mariano R S．Nonlinear filters based on Taylor series expansion［J］．Commu Statist Theory and Methods，1996，25（6）:1261－1282．

［5］ Julier S，Uhlmann J K．A new extension of the Kalman filter to nonlinear systems［C］∥Proceedings of the Soeiety of Photo-Optical Instrumentation Engineers（SPIE），1997:182 －193．

［6］ Julier S，Uhlmann J K，Durrant-Whyte H F．A new method for the nonlinear transformation of means and covariances in filters and estimators［J］．IEEE Transactions on Automatic Control，2000，45（3）:477 －482．

［7］ Arasaratnam Ienkaran，Haykin Simon．Cubature Kalman filters［J］．IEEE Transactions on Automatic Control，2009，54（6）:1254－1269．

［8］ Akashi H，Kumamoto H．Construction of discrete-time nonlinear filter by Monte Carlo methods with variance-reducing techniques［J］．Systems and Control，1975，19:211 －221．

［9］ Handschin J E．Monte Carlo techniques for prediction and filtering of non-linear stochastic processes［J］．Automatica，1970，6:555－563．

［10］ Doucet A，Gordon Neil J，Krishnamurthy Vikram．Particle filters for state estimation of jump markov linear systems［J］．IEEE Transactions on Signal Processing，2001，49（3）:613 －624．

［11］ Doucet A，Godsill S，Andrieu C．On sequential Monte Carlo sampling methods for Bayesian filtering［J］．Statistics and Computing，2000，10:197 －208．

［12］ Lefebvre T，Bruyninckx H，Schutter J D．Kalman filters for nonlinear systems:A comparison of performance［J］．International Journal of Control，2004，77（7）:639 － 653．

［13］ Bell Bradley M，Cathey Frederick W．The iterated Kalman filter update as a Gauss-Newton method［J］．IEEE Transactions on Automatic Control，1993，38（2）:294 －297．

［14］ Kong Xiaoying，Nebot E M，Durrant-Whyte H．Development of a nonlinear psi-angle model for large misalignment errors and its application in INS alignment and calibration［C］∥IEEE International Conference on Robotics and Automation，1999:1430 －1435．

［15］向 礼，柳 明，苏宝库．高斯混合粒子滤波器在静基座捷联惯导系统初始对准中的应用［J］．大连海事大学学报，2008，34（2）:61－64．