多传感器信息融合在滚动轴承故障诊断中的应用

马文龙，吕建新，吴虎胜，黄炯龙

（武警工程大学，陕西西安 710086）

0 引言

滚动轴承作为旋转机械的通用部件，在工农业生产、交通等领域的应用非常广泛，它的运行状态直接影响到整个机械设备的性能、效率和寿命。统计数据显示:旋转机械大约30%的故障是由滚动轴承故障所引起的。因此，研究滚动轴承故障诊断方法具有重要现实意义。

滚动轴承由于制造误差、装配原因、阻尼等多种因素影响而产生的振动信号一般是非平稳、非线性、非高斯的随机信号。经验模式分解（EMD）［1］、小波包［2］、局部均值分解（LMD）［3］等时频分析方法对振动信号不同方面的特征具有不同的敏感度，在信号分析中各具优势，但由于方法本身的局限，也都存在一定缺陷，因此，这3种方法在故障特征提取中都不完善。

多传感器信息融合［4］（有些文献中也称为多传感器数据融合）能综合从多个传感器采集到的故障信息，使诊断结果更加可靠。信息融合按照数据抽象的程度一般分为3种:数据层融合、特征层融合和决策层融合［5］。分析各层次融合方法的优劣，本文选择采用特征层、决策层相互结合的信息融合方法。支持向量机（support vector machines，SVM）相比较其他分类算法来说，在处理小样本、非线性问题时更具优势，而且能够避免局部极值的问题，泛化性能也比较好。因此，本文选择支持向量机作为特征层的故障信息融合中心，而决策层融合则采用D-S证据理论的方法。

1 Dempster-Shafer证据理论

Dempster-Shafer证据理论是由Dempster于1976年首先提出，后由Shafer加以扩充和发展，因此，证据理论又称为 D-S 理论［6］。

1．1 基本理论

设U为一识别框架，m（A）为A的基本概率赋值。表示对命题A的精确信任程度，也就是对A的直接支持程度。

信任函数（belief function）BEL

似真度函数（plausibility function）PL

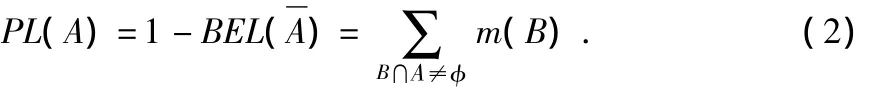
规定的信任区间（BEL（A），PL（A））描述A的不确定性，如图1。

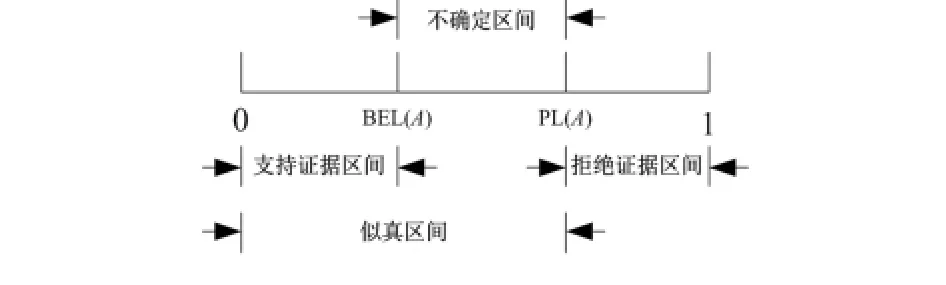
图1 信任区间划分Fig1 Partition of belief interval

1．2 证据理论的组合规则

设m1，m2，…，mn是2U上的n个相互独立的基本概率赋值，通过融合规则可以求解组合后的基本概率赋值m=m1⊕m2⊕…⊕mn，即

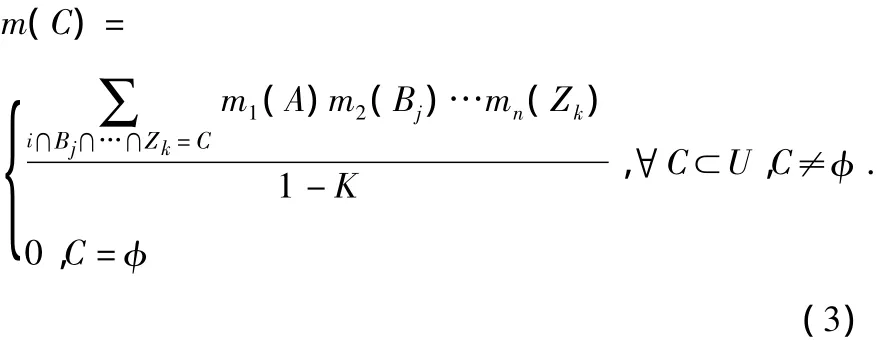
1．3 基于D-S证据理论的决策

用证据理论组合证据后如何进行决策是与应用密切相关的问题。考虑到滚动轴承故障的分布特点，本文决定采用基于概率赋值的决策。

设∃A1，A2⊂U，满足

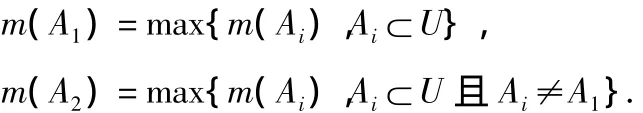
若有

则A1即为判决结果，其中，ε1，ε2为预先设定的门限。

2 SVM后验概率输出

传统的SVM［7］在进行故障判别时，只能确定是否发生故障，即只有确定的2种分类输出［8］。然而，故障诊断逐步向融合诊断方向发展，简单地判断是否有故障，不仅不符合复杂装备的实际情况，而且严重限制了诊断精度的进一步提升。

Platt提出将后验概率看做是Sigmoid函数的形式，然后采用最大似然估计准则，求出函数的参数［9］。

2．1 二分类SVM后验概率输出

SVM的标准输出为

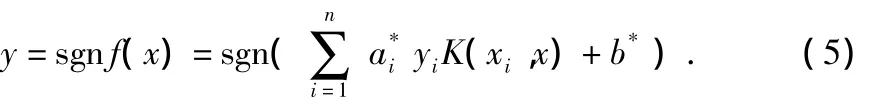
采用sigmoid函数，将SVM的输出f（x）映射到［0，1］，给出了SVM的后验概率输出形式［10］

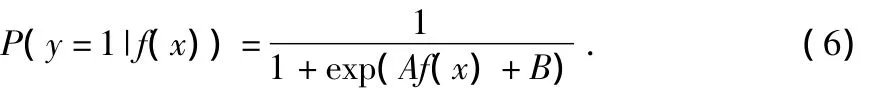
参数估计值为z*=（A*，B*），正样本数用N+表示，负样本数用N-表示，参数A和B可由最大似然估计准则求出

对于多分类SVM，则采用“投票法”对多个二分类SVM的结果进行融合。

2．2 SVM与D-S证据理论的结合

采用证据融合理论进行决策层融合，首要的问题是要确定D-S理论识别框架的基本概率分配（basic probability assignment，BPA）值。

一般用训练样本中平均的支持向量占总训练样本数的比例［11］来得样本分类错误率的期望上界

式中N为训练样本的总数为支持向量个数的平均值。

采用下述方法分配二元SVM的BPA

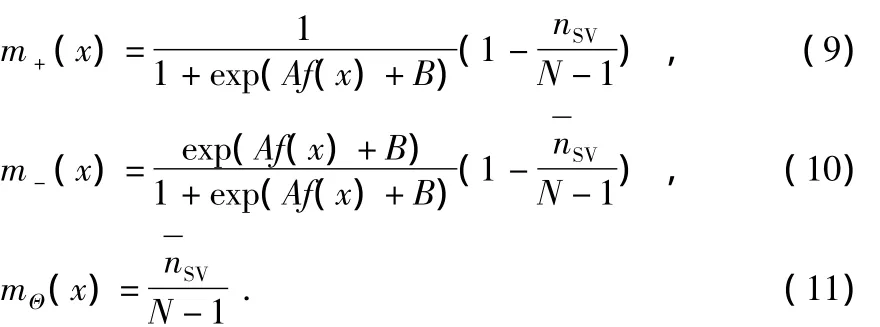
这样就可以实现一个二元SVM的BPA输出。多分类SVM的BPA输出参照二分类SVM的BPA输出得到。

3 多层信息融合故障诊断模型构建

本文在综合分析多传感器各层次信息融合方法优劣的基础上构建了特征层、决策层两级融合诊断的模型。特征层、决策层两级融合的故障诊断模型如图2所示。

图2 两级融合的集成故障诊断模型Fig 2 Integrated fault diagnosis model of two level fusions

信息融合故障诊断过程一般包含3个步骤:数据处理、模式识别、融合诊断。其中，数据处理阶段采用EMD、小波包和LMD的方法对传感器采集到的振动信号进行处理;模式识别阶段采用SVM分类方法构建故障分类器，并以后验概率作为分类器的输出;决策阶段则采用D-S理论进行融合诊断，并依据一定的判别准则，得到决策结果并输出。

从信息融合的意义上讲，SVM属于特征级融合中的特征输入/决策输出过程。而 D-S证据理论是通过对同一识别框架上的各证据体进行融合推理，属于决策级融合中的决策输入/决策输出过程。两级融合的诊断模型能够发挥出各层融合方法的优势，提高诊断的准确性和可靠性。

4 实例分析

本文采用美国Case Western Reserve University电气工程实验室的滚动轴承试验数据来例证本文方法的有效性。测试轴承为6205—2RS JEM SKF深沟球轴承，电机负载为0 HP，轴承工作转速为1797 r/min，故障设置为内圈单点电蚀，外圈单点电蚀和滚动体单点电蚀，增加正常情况，总共采集4种状态的振动信号。采样频率为12 kHz，分析中，每种状态截取80组数据，数据样本长度为2048。

4．1 SVM分类器构建

对原始信号进行降噪预处理，以轴承内圈故障信号为例，选取sym8小波作为降噪用小波，对信号进行3层小波分解与重构。从降噪前后波形图显示降噪后的信号光滑，与原始信号很相似，既去除了部分噪声又较好地保留了故障信息。降噪前后波形对比如图3所示。

图3 降噪前后波形对比Fig 3 Waveform comparison before and after noise reduction

采用EMD、小波包分解、LMD分别对去噪信号进行处理，并提取特征向量。对3种振动信号处理方法得到的数据，各取60个样本，组成训练样本集。每一个样本集经过训练之后，分别得到一个支持向量机故障分类器，分别记为:SVM1，SVM2，SVM3。由于篇幅所限，故障特征提取和支持向量机分类器的训练不做过多叙述。

4．2 故障融合诊断

试验时，采集3只传感器的振动信号，采用上述3种方法分别对振动信号处理，并提取特征向量，然后输入SVM分类器。部分分类识别结果如表1所示。

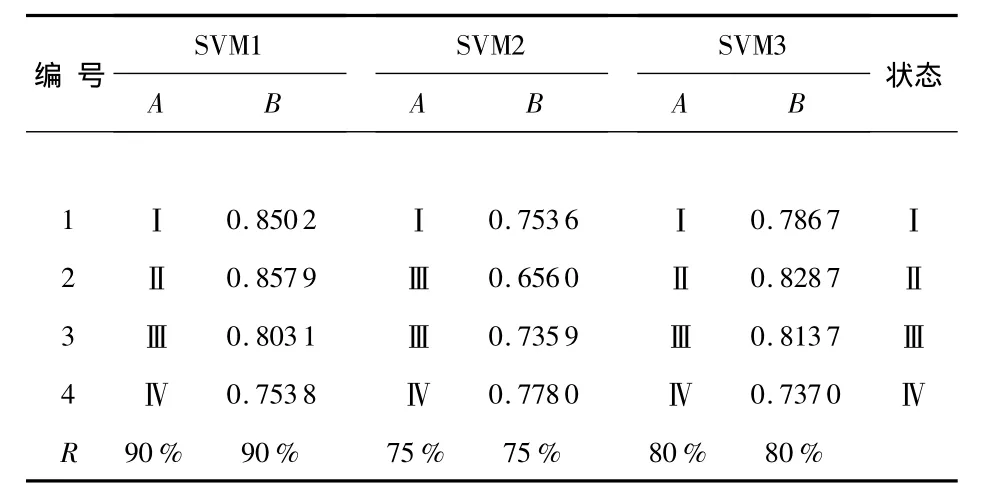
表1 特征层诊断识别结果Tab 1 Result of feature layer diagnosis recognition

判决结果Ⅰ表示正常，Ⅱ表示内圈故障，Ⅲ表示外圈故障，Ⅳ表示滚动体故障。从判决结果来看，3种方法都能实现滚动轴承故障诊断，然而识别正确率不高，甚至SVM2出现了错误识别。比较后验概率和硬判决，后验概率并没有提高识别正确率，再次验证了本文第2节的观点。

根据2．2节介绍的方法，可以将表1中，各分类器的概率输出转换为后验概率的BPA输出，即证据体。部分证据体如表2所示。

表2 部分后验概率BPA输出Tab 2 Part of BPA output of posterior probability

得到证据体后，按照证据融合规则进行融合计算。判决时采用1．3节的判决规则进行判决。其中，ε1取值为0．0001，ε2取值为0．0001。部分判决结果如表3所示。

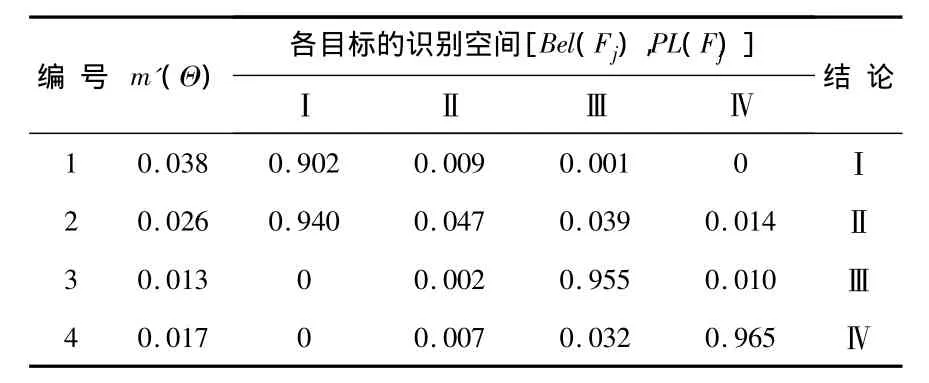
表3 决策层融合诊断结果Tab 3 Result of decision-making layer fusion diagnosis

对比表1和表3，故障识别正确率明显提高，不确定度明显下降。对于表1中出现的错分样本的情况，经过决策融合，也能给出正确诊断结果。

5 结论

本文采用特征层、决策层相结合的信息融合方法，成功实现了滚动轴承故障的诊断。主要结论有:

1）EMD、小波包和LMD在分析振动信号方面各有优势，融合诊断方法能够发挥它们对不同特征的敏感性，有利于充分发掘故障信号的特征。

2）两层信息融合诊断方法，结合不同传感器对故障的判断，能够有效提高滚动轴承的故障识别率，对于其它设备故障诊断具有一定借鉴意义。

3）融合诊断方法提高了诊断系统的可靠性和容错能力，即使单个传感器诊断出现差错时，系统也能给出较为合理的诊断结论。

［1］ 于德介，程军圣，杨 宇．基于EMD和AR模型的滚动轴承故障诊断方法［J］．振动工程学报，2004，17（9）:332-335．

［2］ 王冬云，张文志．基于小波包变换的滚动轴承故障诊断［J］．中国机械工程学报，2012，23（3）:295-298．

［3］ 史美丽．基于LMD的滚动轴承故障诊断研究［D］．长沙:湖南大学，2011．

［4］ 黄漫国，樊尚春，郑德智，等，多传感器数据融合技术研究进展［J］．传感器与微系统，2012，29（3）:5-8．

［5］ 何 友．多传感器信息融合及应用［M］．2版．北京:电子工业出版社，2007．

［6］ Bogler P L，Shafer-Dempster reasoning with applications to multisensor target identification system［J］．IEEE Trans on Systems，Man and Cybernetics，1987，17（3）:968-977．

［7］ 张金敏，翟玉千，王思明．小波分解和最小二乘支持向量机的风机齿轮箱故障诊断［J］．传感器与微系统，2011，30（1）:41-43．

［8］ 杜京义，侯媛彬．基于最小风险的SVM及其在故障诊断中的应用［J］．振动、测试与诊断，2006，26（2）:108-159．

［9］ Platt John C．Advances in large margin classifier［M］．Cambridge:MIT Press，2000．

［10］ Lin Hsuan-tien，Lin Chi-jen，Weng Ruby C．A note on Platt’s probabilistic outputs for support vector machines［J］．Mach Learn，2007，68:267-276．

［11］边肇祺，张学工．模式识别［M］．北京:清华大学，2000．