一种模糊自适应PID控制在溶解氧中的应用*

汤斌斌，陈敏芳，熊伟丽，2，徐保国

（1．江南大学物联网工程学院，江苏 无锡 214122;2．江南大学轻工过程先进控制教育部重点实验室，江苏无锡 214122）

0 引言

在污水处理过程中曝气池溶解氧量的高低直接影响着有机物的去除效率，同时也是影响运行费用和出水水质的重要因素。目前，国内对于溶解氧量的控制一般采用手动或传统的PID的方法，无法满足溶解氧控制系统的非线性、大惯性和难于精确建模等特点。针对这些问题，一些学者对溶解氧控制进行了研究，其中，杨世品、陈林等人提出基于模糊PID控制策略［1］，利用模糊控制原理很好地解决了非线性和难于建模的特点，但模糊控制主要依赖于专家经验，自学习能力较差。于是，胡玉玲、乔俊飞加入了神经网络控制［2］，提高了模糊控制的自学习能力，控制效果较好。

本文提出了一种基于混沌遗传算法（CGA）优化的模糊自适应控制器，并对变参数活性污泥系统范围内任意模型进行仿真实验，考察该控制器的控制性能。

1 曝气池溶解氧量模型仿真

目前，大多数污水处理站采用活性污泥法污水处理工艺，其基本流程包括一沉池、曝气池、二沉池、曝气系统及污泥回流系统，如图1所示。

图1 活性污泥法处理过程简易示意图Fig 1 Diagram of activated sludge processing procedure

对处理系统中的有机底物和微生物等作物料平衡，根据文献［2］得到活性污泥法污水处理过程的基本状态方程为

式中S为曝气池底物浓度，g/m;X为曝气池微生物浓度，g/m3;O为曝气池溶解氧量，g/m3;Si为进水中底物量，g/m3;Xi为进水中微生物浓度，g/m3;Kd为自衰减系数，d－1;^μ为微生物的最大化增长速率，d－1;Y为产率系数，gVSS/gBODs;Yobs为异养菌可观测产率，gVSS/gBOD5;f为有机物与需氧量的一个因子，gBOD5/gCOD;fx为消耗因子，gCOD/gVSS;C为二沉池浓缩系数;u为曝气量，gCOD/gVSS;δ为冲量系数;V为曝气池容积，m3;Q为进水流量，m3/d;QW为排出污泥流量，m3/d。

系统选取曝气量u为控制量，溶解氧量Q（t）作为被控量，并将流入曝气系统的有机物浓度作为干扰，可以将式（1）写为状态方程的形式

其中

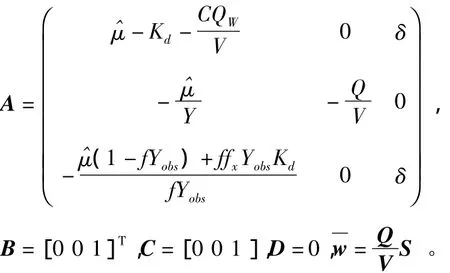
2 模糊自适应PID控制器设计

模糊自适应PID控制器（fuzzy adaptive PID controller，FAPID）由模糊PID控制器、自适应控制器两部分组成［3］，其中自适应控制器的自动组织调整功能由模糊控制器调节，系统结构框图如图2所示。

图中，r为输入值，y为输出值。模糊PID控制器中E，EC和U为控制器输入变量和输出变量，分别是实际误差e、误差速度ec和输出控制量uc对应的模糊变量值。Ke，Kec分别为量化因子，α，β分别为积分和比例因子，则模糊PID控制器输出可表示为

图2 模糊自适应PID控制器结构图Fig 2 Structure of fuzzy adaptive PID controller

控制器采用了PI，PD线性组合方式，在控制器的输入端保留了二位模糊控制器常用的结构方式，后端设计了一个简单加和单元。其中，比例、积分和微分环节分别为αKe+βKecD，βKeP和 αKecD（A，P，D为常数）。

图中自适应控制器是一种基于归一化误差加速度观测器的模糊控制器［4］，以误差的绝对值|e|和系统归一化加速度ev为输入变量，通过模糊输出变量γ1，γ2在线调整模糊PID控制器的微分和积分环节，响应不同阶段的控制要求。如式（3）所示

前段控制f用来观察系统响应过程误差和误差变化，输出为时变因子归一化误差加速度ev，反映了系统变化的快慢，定义如下［5］

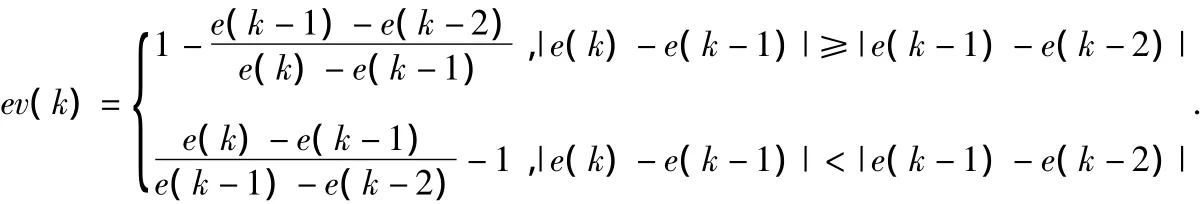
自适应控制器基本论域、模糊子集、隶属度函数设计信息如表1所示。

表1 自适应控制器设计表Tab 1 Form of adaptive controller design

3 基于CGA的控制器参数优化

模糊PID控制器融合可模糊控制和PID控制作用，参数优化设计内容包括控制器结构辨识和输入输出的量化、比例因子，模糊规则与隶属度函数等控制参数调整。其整定过程实际上是一个多参数优化问题。遗传算法（genetic algorithm，GA）通过遗传操作，对种群中的个体实施结构重组，从而不断搜索出种群中个体间的结构相似性，逐步逼近最优解。而遗传算法过早收敛、不能很好保持个体的多样性等缺陷也影响优化设计的正确性和有效性。本文提出了一种在GA寻优过程中加一混沌扰动，利用混沌的“随机性”、“遍历性”及“规律性”等特点［6］避免早熟和局部最优问题的CGA，用来对FAPID的模糊规则与隶属函数进行优化，优化过程如下:

1）用1～7代表输入变量E，EC和输出U的7个模糊语言变量值{NB，NM，NS，ZE，PS，PM，PB}，由于已对输入输出变量的模糊论域做了归一化处理，所以，控制规则库具有对称性，则编码长度可减少至72位，大大缩小搜索空间，待优化控制规则表示为{5 56 567 45666 455677 4455677}。

2）选用三角形隶属度函数，待优化参数表示为{x1ex2ex3ex1ecx2ecx3ecx1uex2uex3ue}，前3位是对误差e的隶属度函数参数的编码，中间3位是对误差变化ec的隶属度函数参数的编码，后3位是对输出uc的隶属度函数参数的编码。

3）本文采用最优化控制设计中常用的ITAE性能指标［7］作为遗传算法优化的目标函数，即

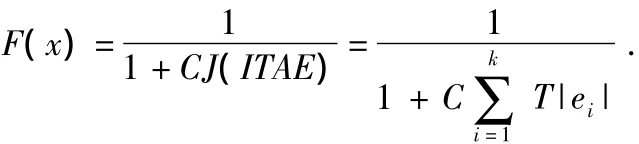
将值域为［0，+∞］的J（ITAE）转换为值域为［0，1］的F（x），其中，C为灵敏控制参数。这样将求ITAE值的极小值问题，转化为求适应度函数的最大值问题。

4）对个体进行二进制编码，然后使上一代中适应度最大的10%不参加复制、交叉、变异3种操作，直接带入下一代群体。另外的90%参加复制、交叉、变异3种操作产生。

5）对子代群体进行解码，计算新的适应度。然后按适应度值对群体进行排序，求出适应度的平均值并与最大值按式（4）比较

如果式（4）成立，则认为寻优过程结束，输出最优值;否则，转入步骤（6）。

6）给当前代群体中适应度较小的90%对应的优化变量按式（5）加一混沌扰动［8］，然后通过算子ψ映射为优化变量，进行迭代计算

式中 λ*为当前最优解映射到［0，1］区间后形成的向量，称为最优混沌向量;λk为当前的混沌向量;λ'k为加了随机扰动后对应的混沌向量。其中，μ按式（6）进行确定

式中 τ为整数，由优化目标函数而定;k为迭代次数。随着迭代次数的增加，式（6）计算出的μ值不断改变，迭代逐渐向较优解逼近，直到前后两次计算出的适应度平均值之差小于预先给定的某个小正数ε2为止。即

式中 经多次仿真表明，取ε=0．5时可以保证混沌扰动的点数大于300，从而保证混沌扰动在解空间的遍历性，k为迭代次数，k=1，2，…。

7）按适应度值对群体进行重新排序，求出适应度的平均值并与最大值按式（4）比较，如果式（4）成立，或进化代数大于最大代数（gnm），则认为寻优过程结束，输出最优值;否则，转向步骤（4）。

4 仿真实验

根据污水处理厂的实际情况，状态方程（2）中的参数是在一定的范围内变化的，属于不确定参数有界系统。以日污水处理能力为2×104m3/d，冲量系数恒取1为例，确定（2）中各参数的上、下界值［2］如式（7）

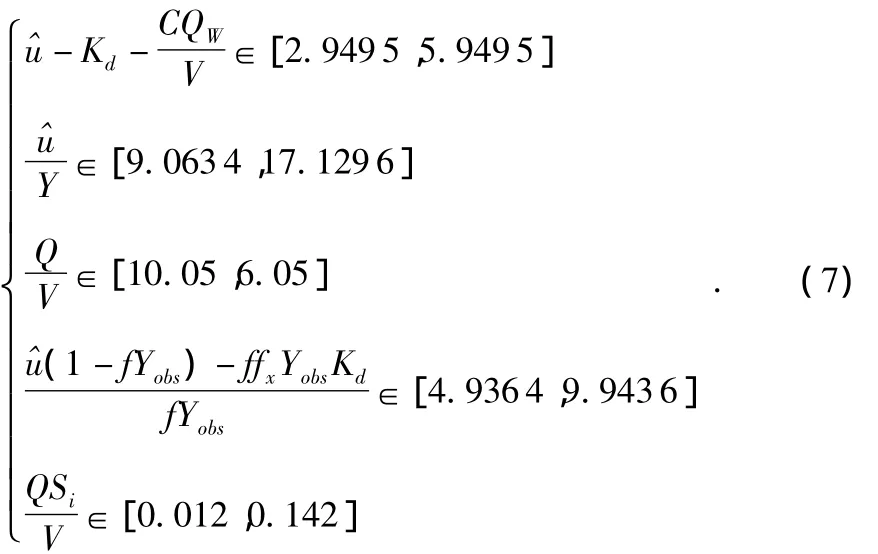
在参数范围内任取参数，系统以下列模型为例对其进行仿真研究

对上述模型进行求解，得到对应的零、极点分别为Z=［－8.0500 3.945 0］，P=［－8.050 0 1.472 5+0.910 9i 1．4725 －0．9109i］，由线性系统理论知识，系统的右半平面存在极点，所以系统模型是内在不稳定的［9］，因此，首先需改善其稳定性能。

系统将状态方程模型的期望极点放置在离虚轴较远的左半平面，分别设为S1，2= －1 ±0．2i，S3= －10，可见S1，2用来满足动态性能的要求，S3为远离虚轴的极点对系统动态性能的影响很小，可以得到模型对应的反馈增益矩阵为

于是，稳定系统的状态方程表达式为

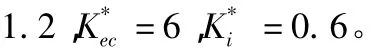
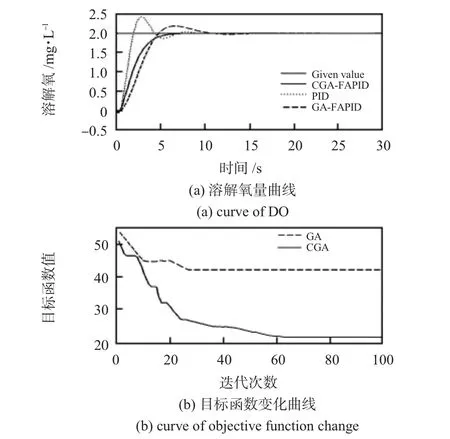
图3 仿真曲线Fig 3 Simulation curve

仿真结果表明:由图3（a）可知，采用CGA优化后的SAPID上升速度快，超调量得到很好抑制，稳态时间缩短。比传统PID和基于GA优化的SAPID控制器在稳态性与动态性能上有了明显的改善，表明了控制系统具有很强的稳定性和适应性。由图3（b）可见，标准GA在28代时陷入局部最优，而CGA有效避免了“早熟”，优化参数更加精确。

5 结论

本文简单介绍了一种模糊自适应控制器的设计，利用GA对控制规则和隶属度函数进行优化，并在寻优过程中加入混沌扰动，提出一种基于CGA优化的模糊自适应PID控制策略，并将其应用于变参数活性污泥系统，通过对范围内任取参数模型的控制仿真表明:CGA与标准GA相比，在保留种群较优个体的前提下，提高了种群个体的多样性，避免了“早熟”和局部最优现象;优化后的SAPID的超调量、上升速度、稳定时间等性能得到明显改善。

［1］ 杨世品，陈 林，李山春，等．基于模糊PID控制的污水处理溶解氧控制系统［J］．仪表技术与传感器，2009（1）:88－90．

［2］ 胡玉玲，乔俊飞．变参数活性污泥系统溶解氧的模糊神经网络控制［J］．电工技术学报，2004，19（3）:36 －40．

［3］ Chen Kuanyu，Tung Picheng，Tsai Mongtao，et al．A self-tuning fuzzy PID-type controller design for unbalance compensation in an active magnetic bearing［J］．Expert Systems with Applications，2009，36（4）:8560 －8570．

［4］ 朱颖合，薛凌云，黄 伟．基于自组织调整因子的模糊PID控制器设计［J］．系统仿真学报，2011，23（12）:2732 －2737．

［5］ Uzelkaya M，Eksin I，Yesil E．Self-tuning of PID-type fuzzy logic controller coefficients via relative rate observer［J］．Engineering Applications of Artificial Intelligence，2003，16（3）:227 －236．

［6］ 唐 巍，郭镇明，唐嘉亨，等．复杂函数优化的混沌遗传算法［J］．哈尔滨工程大学学报，2000，21（5）:1 －5．

［7］ 李 华，马 虬．一种改进遗传算法在模糊控制器优化中的应用［J］．控制工程，2008，15（6）:682 －684．

［8］ 姚俊峰，梅 炽，彭小奇，等．混沌遗传算法及其应用［J］．系统工程，2001，19（1）:70 －74．

［9］ 郑大钟．线性系统理论［M］．2版．北京:清华大学出版社，2005．

［10］张自杰，林荣忱，金儒霖．排水工程［M］．4版．北京:中国建筑工业出版社，2000．