一种新的传感器网络的密钥协商算法

王 亮，王伟欣，张 林

（江西理工大学信息工程学院，江西赣州 341000）

0 引言

伴随社会科技的进步，传感器在人们的日常生活中越来越普遍，能耗问题和安全问题成为无线传感器关注的焦点，而耗电量与密钥的实现方法息息相关。私钥加密体系因为其加密的效率高、速度快被广泛地关注，是如今最常用的数据加密标准［1］。但是，它有不适合用于无线传感器网络的缺点。因为在传感器网络上的节点并不是限制为一对，而是大量的节点。例如:在有n个节点的网络，则需要产生的私有密钥个数为n（n－1）/2。如果n变得很大时，密钥的管理就很复杂，而且这些私有密钥都是在传感器网络上生成，因此，生成密钥并找到安全通道分发密钥就成了传感器网络的负担。

公钥加密体系使用2个密钥，每个节点在网络上发布了一个公共密钥，任何节点都可以用公共密钥来给它们发送消息，同时保持私有密钥进行解密。n个节点通信时，只需要n个私有密钥和n个公有密钥。时间复杂度从O（n2）减少为O（n）。然而，公钥密码系统也有其缺点，它要比私钥加密慢几个数量级别。比如:RSA需要1024位的密钥，椭圆曲线加密（ECC）算法要达到同样的安全级别只需要160位［2］。ECC算法因为存储空间小、处理速度快、计算量小等优点，非常适用无线传感器网络的加密解密。

1 ECC与RSA理论

1．1 RSA 加密体制

在密码学中，RSA（Rivest-Shamir-Adleman）密码体制是一种公钥加密算法。这是目前应用最广的适合签名和加密的算法，普遍认为是最优秀的公钥方案之一［3］，主要用于不安全的通信介质、电子商务协议和服务供应商的身份认证。RSA算法包括3个步骤:密钥生成、加密和解密。RSA使用大小可变的加密块和一个可变大小的密钥，密钥对来自一个大的数n（即根据特殊规则选择的2个素数的乘积），根据会话各方和施加的约束所需要的安全目标实现安全协议。

1．2 ECC 加密体制

ECC密钥对的生成是根据椭圆曲线的参数组T=（m，p，q，G，n，h）。椭圆曲线加密算法以曲线y2=x3+ax+b为基础，其中，a b∈Fq且4a3+27b2≠0。每改变参数p，q就能找到不同的椭圆曲线。密钥对产生后，还需要判断密钥对的合法性。在公钥合法性的判断中，需要判断公有密钥Q是否符合参数组T=（m，p，q，G，n，h）确定的椭圆曲线［4～6］。如果条件不满足就需要重新生成密钥。

1．3 ECC 实现难点

ECC加密中最关键、最耗时的运算就是标量乘，其逆运算为ECC密码体制的离散对数难问题［7］，主要的运算包括ECC加法运算和ECC倍乘运算。

1）加点

令P=（x1，y1）∈E（K），Q=（x2，y2）∈E（K），P≠ ±Q，则P+Q=（x3，y3）。其中

图1 ECC加点运算Fig 1 ECC add operation

2）倍点

当P=Q时，令P=（x1，y1）∈E（K），P≠ －P，则 2P=（x3，y3）。P点的切线和曲线交于R＇，此点在x坐标轴的对称点即为点R。其中

2 RSA和ECC算法

2．1 RSA 算法

2．1．1 生成密钥

1）选取2个足够大的素数p和q，且p不等于q，同时计算n=pq;

2）计算e＇=（p－1）（q－1）;

3）选择e与（p－1）（q－1）互质，e=gcd（e＇，e）=1;

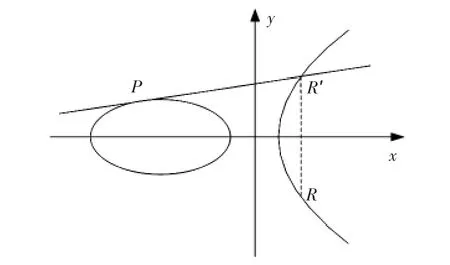
图2 ECC倍点运算Fig 2 ECC point multiplication

4）公式计算d:d=e－1mode＇。

2．1．2 加密

加密公式:c=Me modn，计算c并不复杂，节点A算出c后就可以将它传递给节点B。

2．1．3 解密

节点B获得服务器的消息后，利用自己的密钥d来解码。解密公式:M=Cd modn。

RSA算法的缺点主要有2点:

1）产生密钥耗时太久，受到素数产生技术的限制，因而难以做到一次一密;

2）为保证安全性，n至少也要600 bits以上，使运算代价提高，尤其是速度减慢，较对称密码算法慢几个数量级。

2．2 ECC 算法

2．2．1 初始化环境，并生成密钥

选取基于F2椭圆曲线T=（m，p，q，G，n，h）上一个素数阶n的点G（xp，yp），私钥d∈［1，n－1］，并计算公钥PK=dG;

2．2．2 加密过程

节点A发送信息m给节点B时，节点A执行下列步骤:

1）查找节点B的公钥PKB;

2）将信息m表示成椭圆曲线F2域元素m∈F2;

3）在选取一个随机整数k∈［1，n－1］:

4）计算点（x1，y1）=kG;

5）计算点（x2，y2）=kPKB;

6）计算c=mx2;

7）传送加密数据（x1，y1，c）给B。

2．2．3 解密过程

当节点B解密收到的密文时，执行下列步骤:

1）使用公钥和它自身的私钥dB，计算点（x2，y2）=dB（x1，y1）;

2）通过公式m=cx2，对数据m进行恢复。

为了提高性能，减少计算量，对传统ECC算法做了改进。

2．3 本文改进算法（MAC-F-ECC）

MAC-F-ECC算法和原传统算法相比，增加了Mac地址校验来提高安全性，本文按事先约定好的映射关系从信息m中截取一段作为Mac地址，并使用Frobenius算法代替二进制算法计算kG，减少了运算次数，提高效率。公式（5）为MAC-F-ECC算法倍乘的实现

MAC-F-ECC算法流程图如图3。

图3 MAC-F-ECC流程图Fig 3 MAC-F-ECC flow chart

2．4 性能评估

2）在加密的过程中，将MAC地址身份信息连同消息一同发出进行校验，增加算法安全性。

3 ECC和RSA的比较

3．1 安全性分析

由于传感器的计算能力和存储空间有限，所以，受到密钥长度的限制，ECC体制能通过生成较短的密钥达到较好的安全级别。当然所需带宽显然也减少，并降低了传感器的存储要求和计算负担。最著名的ECC加密技术公司Certieom曾做过实验比较［4］，结果表明:ECC算法所需破译时间要比RSA算法多得多，如图4所示。

3．2 能耗性分析

图4 安全级别Fig 4 Safety level

椭圆曲线的点乘操作是加密过程中最耗时的步骤，减少点乘算法的时间复杂度就在最大程度上节约了能耗。改进的MAC-F-ECC算法降低加点的数量，加快加密算法的计算，如图5所示。

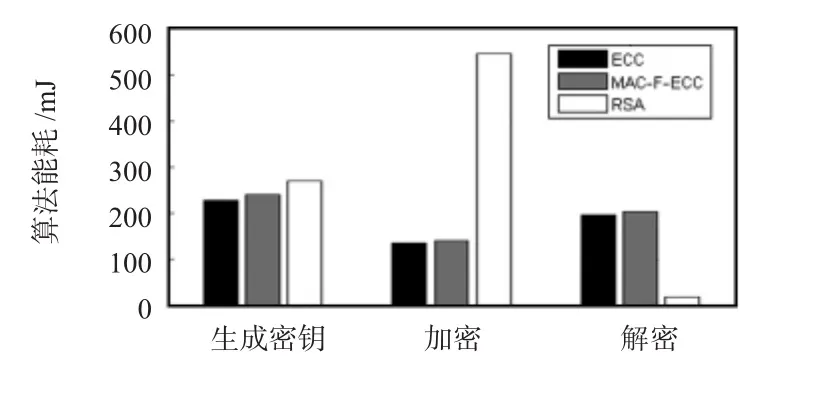
图5 算法能耗对比图Fig 5 Contrast diagram of algorithm energy consumption

3．3 速度效率分析

图6从三加密算法的3个阶段（密钥生成、加密，解密）所需的时间（ms）。仿真效果表明:RSA算法除了在解密验证时速度稍微低于MAC-F-ECC算法，其他阶段MACF-ECC算法都明显其他2种算法，且总耗时要优于传统ECC算法。

图6 各阶段时间对比图Fig 6 Contrast times diagram of each stage

4 结束语

在无线传感器上采用公钥加密体制体质代替原有的私钥加密体制，有着极其重要的意义，文中提出的MAC-FECC算法，通过对其安全性、能耗以及效率的分析可知，该算法能够满足通信节点进行相互身份认证和密钥协商的要求，而且具有安全性高、计算量小、信息量少的特点。正因为MAC-F-ECC算法的这些优势，才能适用于无线传感器网络。

［1］ 丁 宏，郭艳华．一种安全有效的小公钥加密协议及其应用［J］．小型微型计算机系统，2003，24（5）:819 －821．

［2］ 彭长艳等．基于IBC的TLS握手协议设计与分析［J］．计算机应用，2009（3）:633－638．

［3］ 王红珍，李竹林．基于AES和ECC的混合加密系统的设计与实现［J］．电子设计工程，2012，20（4）:9 －11．

［4］ 彭 冰，付 才，付 雄．一种基于椭圆曲线的高效移动支付系统［J］．计算机应用研究，2008，25（9）:2819 －2821．

［5］ 胡 磊，冯登国，文铁华．一类 Koblitz椭圆曲线的快速点乘［J］．软件学报，2003，14（1）:1907 －1910．

［6］ 田 野，盛 敏，李建东．一种新的传感器网络MAC地址分配算法［J］．西安电子科技大学学报，2006，33（5）:716 －720．

［7］ 魏东梅．基于FPGA的F2m域椭圆曲线点乘的快速实现［J］．计算机应用，2011，31（2）:540 －542．