行列式的两点巧用

韩 飞

(咸宁职业技术学院，湖北 咸宁 437100）

行列式是线性代数中的重要内容，在很多领域有着广泛应用。本文结合作者在平时教学中的体会，介绍行列式的两点巧用。

一、巧证微分中值定理

微分中值定理包含罗尔定理、拉格朗日中值定理及柯西中值定理，传统的证明方法是在罗尔定理的基础上，用构造辅助函数的方法证明拉格朗日中值定理，进一步再构造辅助函数证明柯西中值定理，其难点在于构造辅助函数，学生不易想到。利用行列式能巧证拉格朗日中值定理和柯西中值定理。

（一）拉格朗日中值定理

设函数 S(x)表示以曲线上三个点（a，f(a)），（b，f(b)），（x，f(x)）为顶点的三角形的面积（图 1），由面积公式

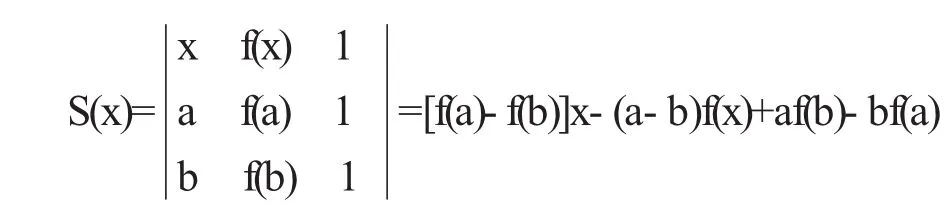
其中:x∈[a,b].

因为 S(a)=S(b)=0，且 S(x)在[a,b]内连续，在（a,b）内可导，因此S(x)满足罗尔中值定理，于是至少存在一点 ζ∈（a,b），使得

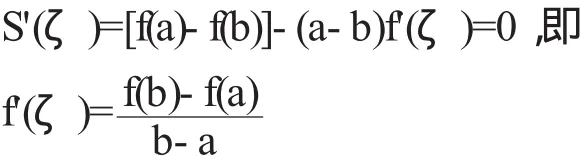
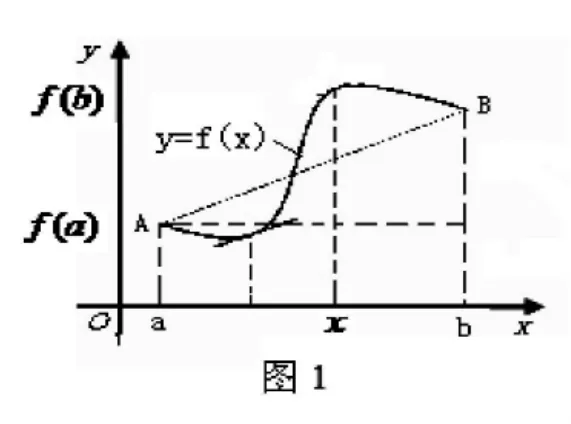
（二）柯西中值定理

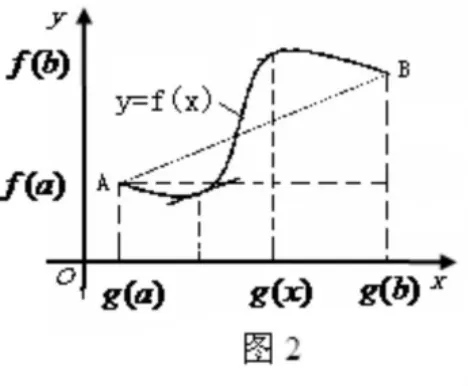
设函数 φ（x）表示以曲线上三个点（g(a)，f(a)），（g(b)，f(b)），（g(x)，f(a)）为顶点的三角形的面积（图2），由面积公式

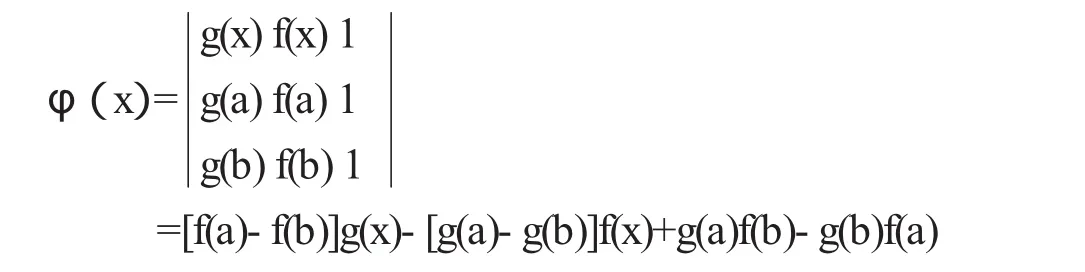
其中，g(x)∈[g(a),g(b)]

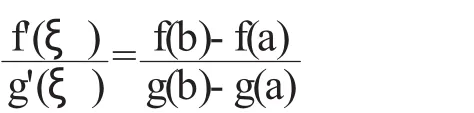
二、因式分解的应用

传统的因式分解的方法有很多，对于一些特殊的多项式，利用行列式分解则更加方便。

解:因为

[1]李飞飞,赵临龙.微分中值定理证明方法[J]甘肃联合大学学报（自然科学版）2012(9).

[2]郭欣红,姜晓燕.经济数学[M]北京:人民邮电出版社,2010.