Matlab软件在单摆自由振动中的应用

李 硕， 赵彤帆， 李根全， 宋海珍

(1.南阳师范学院物理与电子工程学院，河南 南阳 473061;2.河南省教育厅 电教馆，河南 郑州 450004)

0 引言

1 大角度自由振动单摆周期与角振幅的关系曲线

分析一个机械结构的振动特性时需要去掉某些次要因素，把其简化为动力学模型，同时确定其自由度数。以摆动为例，最简单的是保守力场中无阻尼的单摆模型，设悬线长为 l、摆角为 θ(θ＜5°)，取摆长 l=1、重力加速度g=9.8，可以计算出单摆小角摆动时的微分方程为

式(2)是单摆小角摆动时的微分方程，也是简谐振动的动力学方程，式(2)的解为

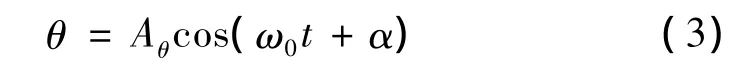
式中，Aθ、α是由初值条件来决定的待定常数。

若大角度摆动，不能近似用sin θ≈θ，微分方程由式(1)改为

小角度单摆的周期为

改变摆角的大小，用数值计算法和相图法研究大角度单摆的周期变化。通过求解式(4)的数值解和已有的实验研究[12]，得到在大摆角下单摆周期与角振幅的关系

利用Matlab画图我们可以清楚的看到大角度单摆的周期变化，结果如图1、2所示。

大数据背景下，市场营销的内涵得到了明显的更新，在这种情况下，企业就应积极地创新营销方式，将企业文化、理念、信誉以及服务进行有机的融合，销售给消费者以及一切潜在的客户，最终在完成产品交易的同时，传播企业文化，真正实现品牌营销。除此之外，企业还应不断增加品牌价值，加大宣传以及展示力度，促使企业营销管理能够紧随大数据时代的发展，树立良好的企业核心竞争力。

图1 大角度单摆的周期变化

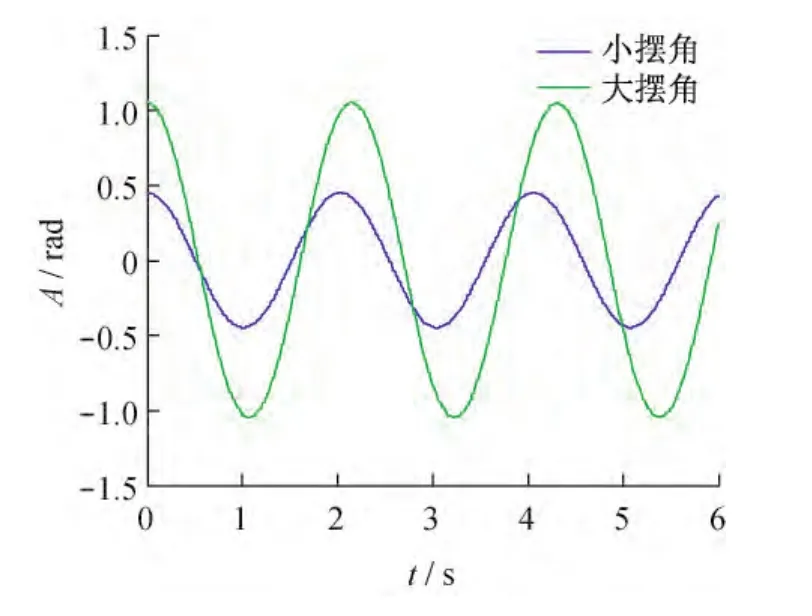
图2 不同摆角的位移曲线

图1表示角振幅A(最大摆角)在0，π()/2内变化时相对应的周期变化，随着角振幅增大，周期不断变大。图2说明在无阻尼情况下，小角度和大角度单摆都呈周期性变化，角振幅越大周期越长。图1和图2所表现的结果符合式(6)。

2 大角度自由振动单摆的相图

在单摆的摆动问题中，系统自由度为1，选取广义坐标θ来描述单摆的运动。系统动能为，势能为 V=mgl(1 －cos θ)，能量关系为

由式(7)可以得到角速度

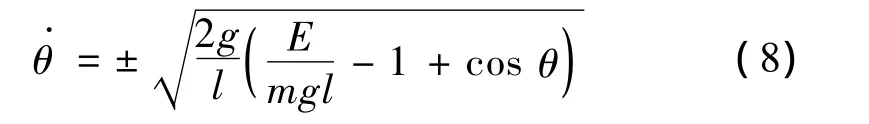
式(8)给出了角度和角速度的关系，使用Matlab软件，根据式(9)画出图3中单摆不同能量下的运动状态。

相图是相平衡系统和一些参数(能量、角度、角速度)的关系图，图像可以方便地判断系统的稳定性，渐近稳定性等。E＜2mgl，单摆能量较小，其轨迹为一闭合的椭圆曲线。E＞2mgl，摆在势场中作定向运动，其轨迹是两条不相交的曲线，θ可以趋向 ±∞。E=2mgl，运动出现了临界状态(图3中曲线的交点，即鞍点)，下一刻的运动具有不确定性，由此出现了非线性现象[13]，在非线性振动中，轻微扰动会使系统出现间断和分岔。

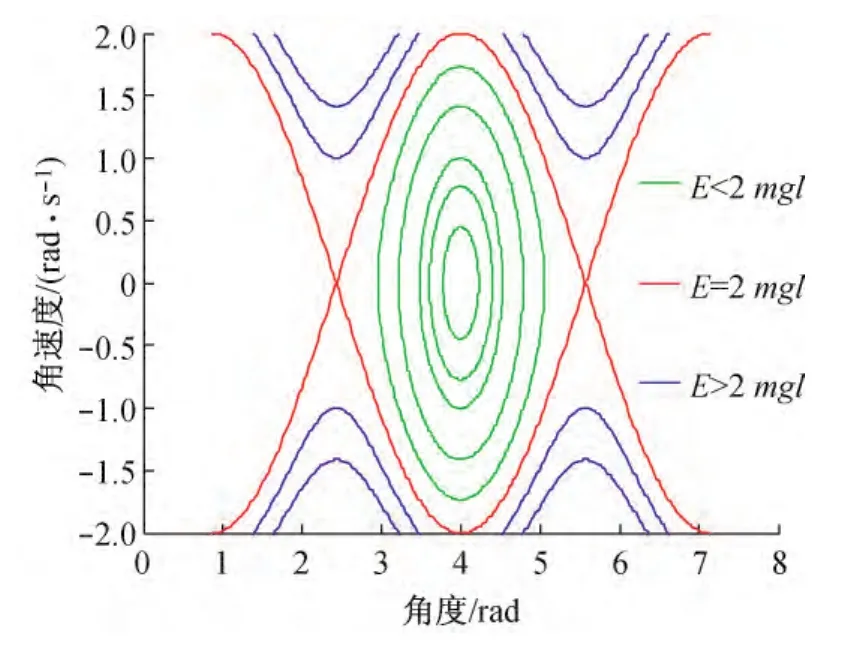
图3 不同能量单摆的相图

3 大角度阻尼振动单摆的相图

如果考虑阻尼影响，将式(4)改为

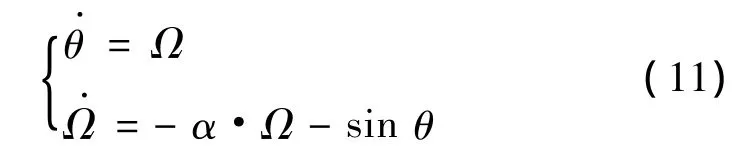
对于耗散系统，研究的是系统长时间的行为。根据式(11)，用Matlab软件绘制阻尼振动单摆的相图。

图4(a)中说明单摆的在耗散系统中出现了混沌，这种集合环绕形象称为“奇怪吸引子”。对于相图中的混沌轨道，可以看出在保守系统中能量的耗散。比较图4(a)和(b)，阻尼系数做微小的改变，对系统进行轻微扰动，长时间后的变化却是巨大的，这体现了混沌现象的随机性和不可预测性。

图4 有阻尼单摆的相图

4 弹簧单摆微分方程的求解及动画效果

设质量为m的摆球挂在劲度系数为k的轻弹簧上，弹簧原长为l0，则系统静止时弹簧自然下垂长度为l=l0+mg/k，让摆在竖直平面内自由摆动。系统自由度为2，设r为摆球到固定点的距离，摆角为θ。系统的拉格朗日函数为

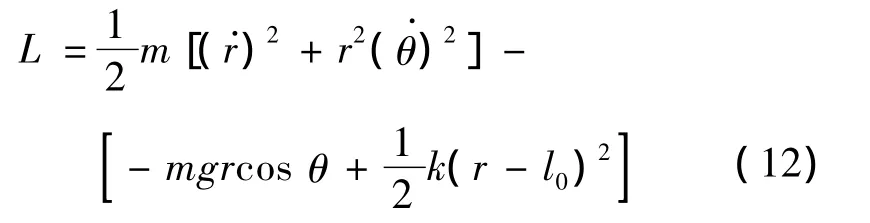
由式(12)根据Lagrange方程求出系统的微分方程

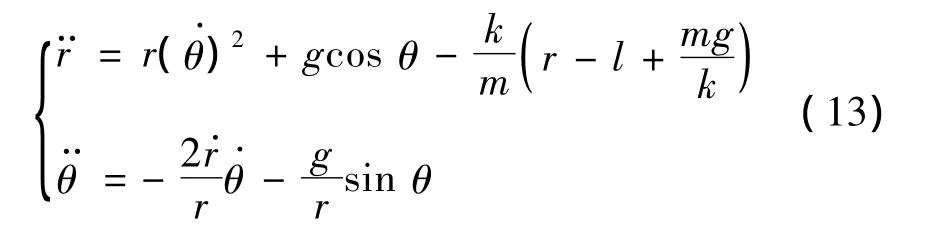
为了方便程序的编辑，令 y1=r，y2=，y3= θ，y4=，将式(13)改写为

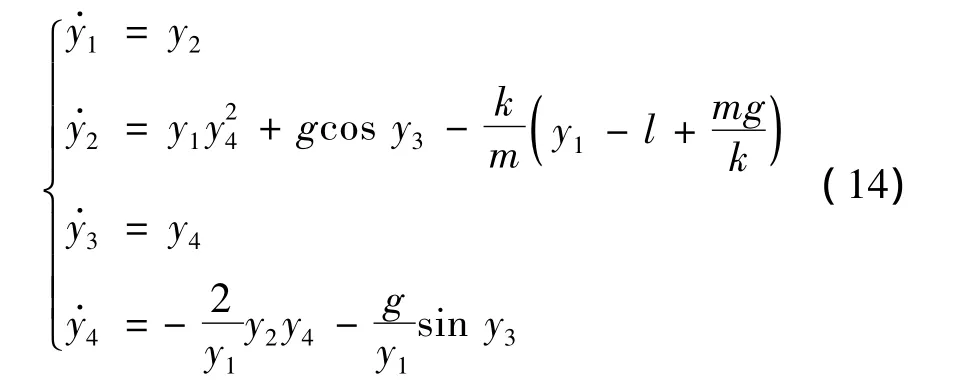
给出弹簧单摆编辑程序，了解如何求解简单的微分方程数值解，建立M文件，文件名存为thb_rk4_5.m，程序编辑如下:

在命令窗口输入:

时间的终点可以自由改动，所得的数值解可以得到变量之间的关系图。程序中设定y1、y2、y3、y4的初值均为 1，即当 r(0)=1(0)=1 时得到图5(a);当(0)=1(0)=1 时得到图5(b)。

Matlab软件用于求出微分方程的数值解，简化了传统计算微分方程的复杂性[14]。图5中可以清楚地看到在一定时间内，角度、角速度的变化。在角度趋近零度时，总摆长总是有增大趋势。说明摆长和角度不是简单的线性关系，与弹簧的劲度、角速度都有关系(通过改变劲度、角度、角速度任一系数可以观察相图变化)。Matlab软件选取不同的参数[15-16]，可以观察所选取参数的变化规律。

弹簧摆的运动由于实验器材带来的误差，使得实验效果不佳，在教学过程中，可以利用Matlab软件的3D视图动画效果观察摆动现象，如图6所示，使用pause命令设定摆动时间。

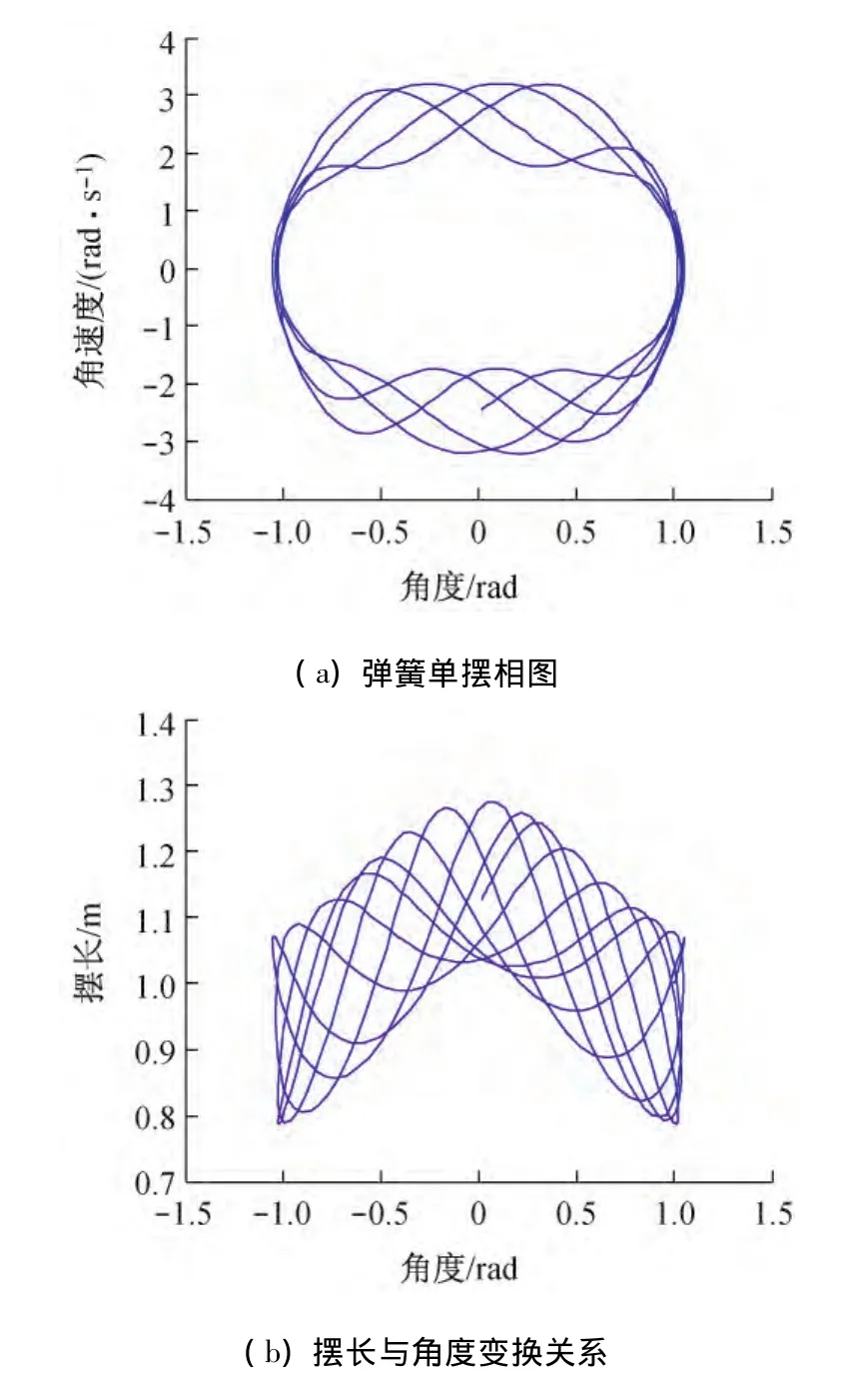
图5 求解弹簧摆微分方程数值曲线

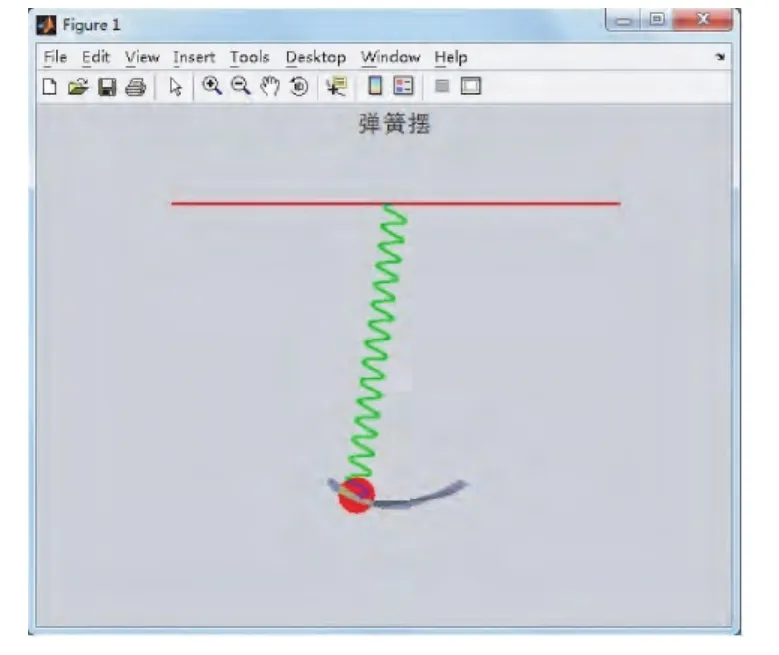
图6 弹簧摆的动画效果

图6是弹簧摆的动画，摆球下面的曲线是摆球运动的轨迹，使用Rotate 3D命令可以拖动图像旋转，可以从不同角度观察，这种视图效果可以直接看到摆动效果，而且弥补了实验带来的操作误差。

5 结语

本文以单摆自由振动为例，展现了Matlab软件在微分方程求解、动画视图、计算结果可视化方面的应用。结果表明，用Matlab处理自由振动问题，可使计算快捷高效，计算结果物理意义清晰，而且大大提高了同学们的学习兴趣和自学能力。

[1] 王振发.分析力学[M].北京:科学出版社，2003.

[2] 刘式达，梁福明，刘式适，等.自然科学中的混沌和分形[M].北京:北京大学出版社，2003.

[3] 胡盘新，钟季康.在大学物理教材中引入计算机数值解的尝试[J].物理与工程，2006，16(2):47-50.

[4] 宋海珍，卢 成，张鸿军.基于Maple的理论力学教学实践[J].实验室研究与探索，2011，30(7):11-14.

[5] 吕秀丽，牟海维，李贤丽.Matlab在电磁场与电磁波实验教学中之应用[J].实验室研究与探索，2010(2):110-112.

[6] 程 铃，徐冬冬.Matlab仿真在通信原理教学中的应用[J].实验室研究与探索，2010(2):117-119.

[7] 鲁兴举，彭学锋，郑志强.提高自动化专业学生工程素质-以倒置摆实验为例[J].实验室研究与探索，2011，30(10):272-275.

[8] 刘亮元，贺达江.电磁场与电磁波实验教学[J].实验室研究与探索，2010，29(5):30-32.

[9] 宋海珍，，张鸿军，卢 成.基于Maple软件的理论力学可视化教学探索[J].实验技术与管理，2011，29(1):93-95.

[10] 张 威.MATLAB基础与编程入门[M].西安:西安电子科技大学出版社，2008.

[11] 吕良军，杨胜用.Matlab在大学物理中应用的几个实例[J].中国科技信息，2008(19):250-251.

[12] 王志伟，李闯国.大角度下单摆周期变化的实验分析[J].青海大学学报(自然科学版)，2007，25(2):92-94.

[13] 符五久，饶黄云.单摆系统通向混沌的道路[J].大学物理，2008，27(1):5-10.

[14] 尹新国，杨远贵，公丕峰，等.倒置摆的运动研究[J].大学物理，2010，29(11):16-20.

[15] 杨正波，夏清华，刘思平.不同控制参数下的弹簧摆[J].大学物理，2011，30(5):23-26.

[16] 杨正波，夏清华，刘思平.多弹簧振子耦合系统运动研究[J].大学物理，2010，29(4):29-32.