我国城镇居民消费支出结构性差异研究

曾 光，王选华，王玲玲

（1.辽宁工程技术大学工商管理学院，辽宁 葫芦岛 125105；2.中国人事科学研究院，北京 100101；3.安得膜分离技术工程(北京)有限公司，北京 101312）

0 序言

当前，由于美国金融危机、欧洲债务危机以及日本大地震等诸多因素共同影响，全球经济的复苏趋势正面临大量的不确定性，欧美等发达地区失业率居高不下，只有新兴经济体和发展中国家的经济仍然维持较高速度的增长。按照国际货币基金组织（IMF）的预测，2012年世界经济增速将达到4.5%，但是，由于经济复苏的不确定性增加，对未来经济增长的前景普遍并不看好。对于我国来讲，在全球金融危机的冲击、出口大量萎缩的条件下，政府及时出台以刺激内需为主的宏观经济政策，近年来宏观经济保持了平稳较快发展。据国家统计局最新发布数据，2011年我国GDP同比增长9.2%，总量达到47.1564万亿元，其中，最终消费对GDP增长的贡献率达到了51.6%，社会消费品零售总额实际增长了11.6%，说明我国近年的刺激内需政策发挥了一定效应。如何进一步扩大内需，维持国内消费需求尤其是居民消费的稳定增长，一直是国内学者长期关注的热点。本文在对国内居民消费文献研究的基础上，使用2010年度城镇家庭人均消费支出数据，通过因子分析方法来讨论城乡居民消费支出的结构与区域性特征，以期能为未来时期政府制定消费需求政策提供参考。

1 研究设计

1.1 研究方法

本文使用因子分析法来考察我国城镇居民的消费结构变化，其基本思想是，将影响城镇居民消费支出的八项指标综合为少数几个公共因子，并利用原始指标与公因子之间的关系来再现消费支出的结构特征。在具体处理上，以相关矩阵的内部关系研究为基础，找出影响居民消费结构的综合指标，这就是公共因子。公因子与原始指标之间的关系即构成如下因子模型：

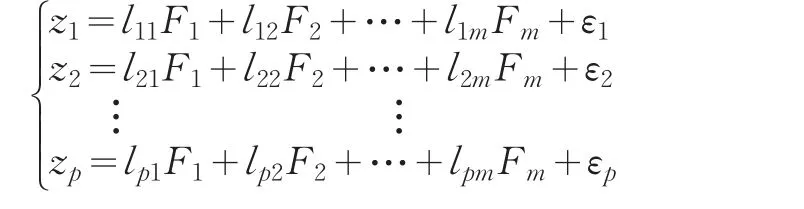
其中，z1，z2，…，zp称为原始变量，F1,F2,…,Fm为公因子，e1,e2,…,ep是特殊因子，已经包含了随机误差项，ei仅与第i个变量zi有关，lij称为第i个原始变量zi在第j个因子Fj上的因子载荷，由其构成的矩阵L称为因子载荷矩阵。本文使用软件SPSS19.0从四个方面开展因子分析：（1）构建原始指标矩阵Z，并将其标准化为矩阵Z′，并计算出相关系数矩阵R；（2）求解相关系数矩阵的特征方程 R-λI=0，得到特征值 λi，并按照 λ1＞λ2...＞λn＞0的条件，以方差累计贡献率一般在85%以上为原则确定公因子的个数；（3）计算特征向量以及因子载荷，并提取特征值大于1的因子作为进一步分析使用的公因子；（4）分别计算所提取的公因子得分和综合分数，以此为依据对31个地区进行分类比较。

1.2 数据来源及指标选取

本文选用的样本数据来源于《中国统计年鉴2011》分地区城镇居民消费支出结构数据，共涉及31个地区、八项消费支出：食品（z1）、衣着（z2）、居住（z3）、家庭设备用品及服务（z4）、医疗保健（z5）、交通和通信（z6）、教育文化娱乐服务（z7）、其它商品和服务（z8），由于所有数据均是2010年度的截面数据，地区之间具有可比性。

2 研究过程

2.1 因子提取过程

为了准确确定因子载荷，消除原始变量的方差过大对其产生影响，我们先对原始指标矩阵Z进行标准化处理，得到标准矩阵Z′（过程及结果略），并求出标准化矩阵的相关系数矩阵R（过程及结果略），并对其结果进行KMO检验和Bartlett球形检验，结果见表1。

表1 我国城镇居民消费支出结构数据的KMO and Bartlett检验结果

按照Kaiser给出的使用KMO取值来选取原始指标作因子分析的判断标准，当KMO＞0.8，Bartlett检验值中，sig.＜0.05时，原始指标相关性较强，适合作因子分析。从本文的检验结果来看，2010年度我国城镇居民消费支持结构数据适合用于因子分析。也可以根据相关矩阵系数矩阵中的取值来判断，本文相关系数矩阵中绝大多数系数值都在0.3以上，说明原始指标之间具有较强的相关性，适合用作因子分析。此外，还可以根据逆像显示的相关矩阵主对角线上元素的值来判断，本文的逆像显示的相关矩阵主对角线上的数值分别为 0.859，0.733，0.861，0.880，0.785，0.862，0.903，0.909，这些数值相对于非对角线上的数值大得多，说明八项原始指标适合用于因子分析。从得到的公因子共同方差来看，八个变量的方差均在0.8以上，说明原始变量所丢失的信息较少，几乎都包含在共同因子中，原始数据使用因子分析的效果较好。

根据相关系数矩阵R计算出特征值及对应的方差贡献率，其结果见表2。

表2 相关系数矩阵特征值与方差贡献率

依据表2，我们依据特征根λi≥1，且累积方差贡献率大于或等于85%的变量作为公因子，故特征根λ1和λ2符合要求，它们所对应的方差贡献率分别为72.286%和15.045%，二者累积方差贡献率达到87.331%，说明前两个公因子可以解释原始变量的信息量超过了87%，从8个公因子中提取前两个公因子是比较科学的，而公因子的碎石图如图1所示。

从图1来看，仅有前两个公因子的特征值大于1，从第三个公因子起，其特征值逐渐递减，选择前两个公因子来满足分析的需要。

图1 我国31个地区城镇居民消费支出公因子特征值碎石图

2.2 因子载荷分析

在提取公因子后，我们将确定变量在所提取公因子上的载荷。从最初公因子载荷来看，八个变量在第一个公因子（F1）上的载荷都很高，表明这些变量同第一个公因子高度相关；变量在第二个公因子（F2）上的载荷相对较小，如表3所示。

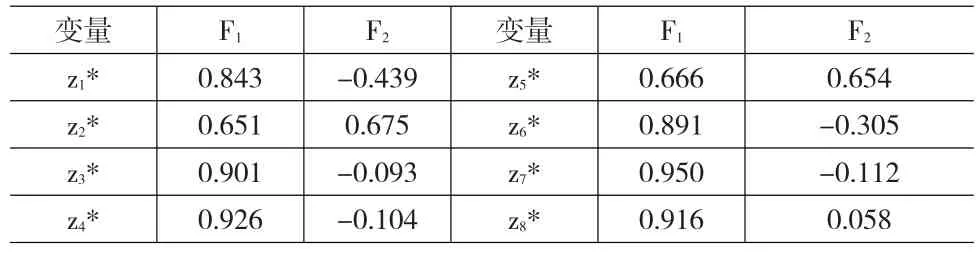
表3 变量在公因子上的初始载荷（旋转前）

一般情况下，要求所提取的公因子之间的相关性较低，或者不具有相关性，从而使公因子之间相互独立，这样才能对每个公共因子赋予清晰的含义。因此，我们对因子负荷矩阵进行最大方差正交旋转，因子负荷矩阵旋转后，可以使在一个公因子上的高载荷变量数量降到最低，从而增强了公因子的解释性。从表3来看，这两个公因子的实际含义比较模糊，无法对其进行清晰的命名，对公因子进行旋转后得到的矩阵如表4所示。

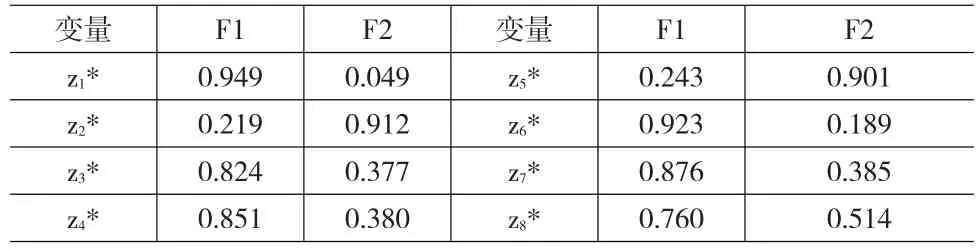
表4 变量在公因子上的初始载荷（旋转后）

从表4来看，旋转后得到的因子负荷矩阵，公因子的含义比较明确，据正交负荷矩阵中的高载荷分布特征，两个公因子的经济含义可以命名如表5。

表5 公因子名称

从表5来看，食品、居住、家庭设备用品及服务、交通和通信、教育文化娱乐服务、其他商品和服务这六项指标在第一个公因子F1上的载荷很高，说明第一个公因子既反映了我国各地区居民一般生活必须品的消费支出，如食品、居住、家庭设备与服务、交通通信以及教育支出等，同时也反映了享受型的生活支出，如接受娱乐服务；衣着、医疗保健等指标在第二个公因子上的载荷很高，表明第二个公因子反映了气候型因子，因为各地区的气候不同，将导致不同的消费支出。

2.3 公因子得分计算

为了讨论消费支出的结构性特征，我们需要通过计算公因子的得分来对地区之间进行比较。公因子的得分系数矩阵如表6所示。

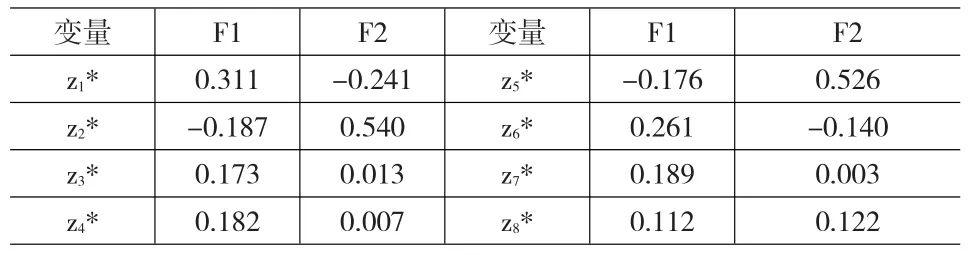
表6 公因子得分系数矩阵

根据表6给出的公因子系数，再结合原始变量标准化后的矩阵来计算两个公因子的得分，并根据公因子的得分结果来对地区之间进行比较分析，以便发现不同地区居民消费支出的结构性特征。因此，公因子得分函数为：

其中，SF1、SF2分别为全国31个地区在公因子F1、F2上的得分；z1*～z8*是原始矩阵Z标准化后的数值。

为了进行综合比较，还需要将这两个公因子以各自的方差贡献率占累积方差贡献率的比重为权重来加权计算综合得分，综合得分函数为：SF=（72.286 SF1+15.045 SF2）/87.331。计算结果如表7所示。

表7 全国31个地区消费支出因子得分及排序

2.4 因子结果分析

表7分别按照两个公因子及综合得分进行排名，从结果来看，对于第一个公因子来讲，东部地区的得分普遍较高，东北和中部地区得分一般，而西部地区较低；第二个公因子得分，北方地区普遍偏高，南方地区相对较低，这主要是受天气的影响，气候较为严寒的地区用于衣着、医疗保健方面的支出占消费支出总额的比重较高，而气候较为温和的南方地区则相反。我们将31个地区按照F1和F2的得分为标准作散点图，如图2、3所示。图2反映了一般生活支出占总支出的比重，图3反映了受气候影响的消费支出比重。

图2表明，上海、广东和北京用于一般生活性支出占总支出比重较高，而这个公因子包含了6项指标，占总消费支出的比重较大，所以可以反映各地区的综合性消费支出。因此，综合性消费支出占比较高的还有浙江、福建、天津和安徽。黑龙江在最下边，说明该地区的城镇居民综合性消费支出较低。如果按照F1得分的标准进行分类，可以将用日常生活和享

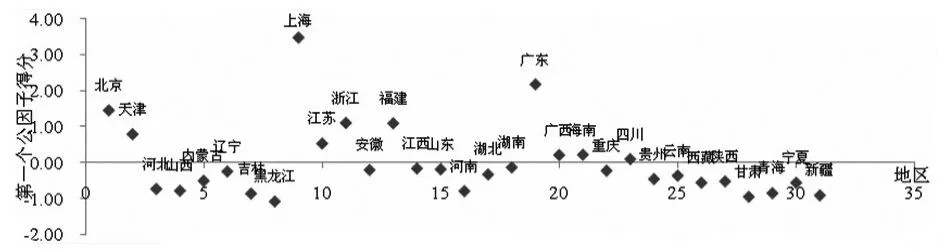
图2 全国31个地区一般消费支出散点图（按照F1得分）

受娱乐的消费支出的地区分为三个集团。将F1得分在0以上的地区视为第一集团，共有10个地区，分别是上海、广东、北京、浙江、福建、天津、江苏、海南、广西和四川，在得分较高的地区中，除了广西和四川属于西部地区经济水平较低的地区以外，其他8个地区都是经济比较发达的东部沿海地区；将F1得分在-0.05～0之间的地区以上的地区视为第二集团，也有10个地区，分别是湖南、江西、山东、安徽、重庆、辽宁、湖北、云南、贵州和内蒙古，位于这一集团的大部分地区都是中部地区，也有部分西部地区和少量的东部地区；将F1得分低于-0.05的地区视为第三集团，共有11个地区，分别是陕西、西藏、宁夏、河北、山西、河南、青海、吉林、新疆、甘肃和黑龙江，第三集团的特征是，大部分地区都属于经济发展相对落后的地区，其中西部和东北地区占主要部分，也有少部分中部地区。

从图3来看，内蒙古和北京最靠上边，说明这两个地区用于御寒的消费支出占总支出比重较高；海南省在最下边，受气候影响的消费支出占比较低。我们以公因子F2得分区间为标

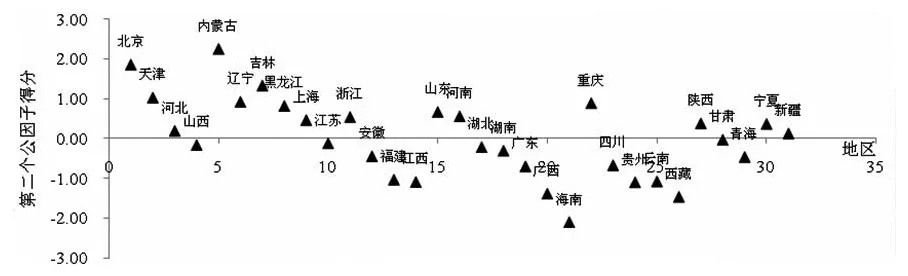
图3 全国31个地区受气候影响的消费支出散点图（按照F2得分）

准来对消费地区进行分类，将F2得分大于0的地区列为第一集团，这些地区分别是内蒙古、北京、吉林、天津、辽宁、重庆、黑龙江、山东、河南、浙江、上海、陕西、宁夏、河北和新疆等15个地区。从这些地区来看，由于受气候影响消费支出比重较高的地区绝大部分都是北方地区和西部气候寒冷地区，如用于购买衣服和医疗保健方面的支出占比较大。此外，这一集团中也有部分南方地区，如上海、浙江、重庆等，如果仅仅使用气候条件来解释这三个地区的消费支出，我们认为未必客观，因为三个地区的一年中的气候相对来讲比较温和，但是在受气候影响的消费支出中，医疗保健是也变量之一；此外，部分衣着支出增加不一定是因为气候原因，而是地区时尚或者其他原因引起。因此我们认为部分南方地区主要因为时尚因素或医疗保健支出较多，从而导致该部分支出比重较大，而并不是为了御寒购买衣服的支出增加。

我们以表7中综合因子得分为标准来将全国31个地区的消费支出进行分类。将综合因子F得分大于0的地区列为第一集团，分别是上海、广东、北京、浙江、天津、福建和江苏等7个沿海经济发达地区；综合因子得分大于-0.05小于0的地区是第二集团，主要有15个地区，分别是内蒙古、重庆、四川、山东、辽宁、广西、湖南、海南、安徽、湖北、江西、陕西、宁夏、吉林和云南。在这综合消费支出的第二集团中，大部分地区都位于中部地区和西部地区，只有山东省来自东部地区；综合得分小于-0.05的地区有9个，这些地区是河南、贵州、河北、山西、西藏、新疆、黑龙江、青海和甘肃，消费综合支出落后的地区几乎都是经济水平不发达地区，这一集团的部分地区虽然由于受气候影响而增加消费支出的比重较大，但是用于一般生活消费、娱乐支出较少，从而导致综合消费支出费用较低。

3 结论与政策建议

本文使用因子分析技术研究了我国31个地区城镇居民消费支出的结构特征，得出以下结论：一是我国城镇居民消费支出的规模主要受地区经济发展水平和气候等两个因素影响。对于经济发展水平较高的沿海地区，用于一般生活支出、娱乐支出的比重较高；气候寒冷的北方地区，城镇居民用于衣着、医疗保健支出的比重较高。二是部分西部地区近年消费支出水平位居前列，如广西和四川两个地区的一般消费支出和娱乐支出占总消费支出的比重位于全国第一集团，而在综合消费支出中，除了四川和广西以外，还有内蒙古、重庆、陕西、宁夏和云南等地区近年的消费支出较高，高于大部分中部地区。三是个别地区消费支出的特殊性。比如，在讨论受气候影响的地区中，衣着和医疗支出受到影响最大的15个地区中，有12个地区都属于北方，而还有上海、浙江和重庆三个南方地区。因此，衣着支出增加在个别地区也并不一定就是气候原因，还可能是时尚等元素导致。

因此，我国政府在制定刺激内需的消费政策时，要针对不同地区的特征有的放矢出台相关政策。对于经济发达地区，在刺激一般性消费支出时，还要为当地居民提供较多的文化、休闲、娱乐等特殊性消费品，进一步扩大发达地区的消费规模；对于西部地区而言，可以通过减少消费税收的形式刺激一般消费需求，以此进一步提高经济落后地区城镇居民的消费水平；对于上海、北京、重庆以及经济发达的其他地区具有较强的时尚消费需求意愿，政府可以有重点地引导具有地方特色的时尚产业发展来刺激消费需求。

[1]吴栋,李乐夫,李阳子.近年居民消费结构统计分析的研究综述——关于因子分析和聚类分析的应用[J].数理统计与管理,2007,(9).

[2]王学民.我国各地区城镇居民消费性支出的分析研究[J].财经研究,2002,(1).

[3]孙冰,王其元.我国居民家庭消费支出结构的对比分析[J].哈尔滨工业大学学报,2002,(8).

[4]宁自军.因子分析在居民消费结构的变动分析中的应用[J].数理统计与管理,2004,(11).

[5]孙艳玲.我国农村居民生活消费实证研究[J].农村经济,2003,（12）.

[6]王芳,王景东.我国城镇消费结构的因子分析[J],商业研究,2004,(21).

[7]纪荣芳.城市居民消费结构的因子分析模型及应用[J].山东农业大学学报(自然科学版),2007,(2).

[8]庄燕君.区域产业结构与消费结构关联分析[J].统计与决策,2005,(1).

[9]申秋红.基于层次分析法的农村居民消费结构研究[J].财贸研究,2007,(5).

[10]殷玲.我国居民消费行为的实证分析[J].商业研究,2004,（20）.

[11]孔祥利,马丽霞.基于面板数据的陕西省农村居民消费结构分析[J].统计与信息论坛,2011,(10).