风险指标与灵敏度相结合的重合时序策略协调
孙士云,束洪春,于继来
(1.昆明理工大学 电力工程学院,云南 昆明 650500;2.哈尔滨工业大学 电气工程系,黑龙江 哈尔滨 150001)
0 引言
自动重合闸装置作为提高输电可靠性和暂态稳定性的有效措施之一,已取得广泛应用[1]。实际应用中的重合闸采用检无压侧首先重合的方式,这是依据电力系统安全稳定导则与电气操作导则,并结合当前重合闸技术的实际应用水平制定的。出于解决两侧断路器工作条件不对等这一问题的考虑,实际中通常由线路首、末端轮换投入同步检定首先重合[1]。
重合闸投入时序对交直流电力系统的暂态功角稳定性 TAS(Transient Angle Stability)和暂态电压稳定性 TVS(Transient Voltage Stability)存在较大影响[2-3]。文献[4-5] 在揭示重合时序对交直流混联输电系统暂态功角稳定性影响规律的基础上,提出了使转移电抗较小的一侧首先重合的时序整定策略,可改善系统暂态功角稳定性。文献[6-7] 在揭示重合时序对交直流混合电力系统暂态电压稳定性影响规律的基础上,提出了考虑负荷模型和故障位置的重合时序整定策略,可改善系统暂态电压稳定性。
文献[4-7] 分别从暂态功角、电压稳定角度提出了相应的重合时序整定策略,适用场景有所不同:提高系统暂态功角稳定性的策略主要用于对系统暂态功角稳定性影响较大的线路,如构成电网主网架的输电线路和区域联络线等;而提高暂态电压稳定性的策略主要考虑重负荷或无功支撑不足的节点。因此,暂态功角和电压稳定视角下的重合时序策略冲突时需进行协调。本文从风险角度出发,提出了风险指标与重合时序灵敏度相结合的重合时序协调方法。
1 全局与局部风险指标
电力系统风险评估的一个显著特点就是能够反映系统及其事件的不确定性本质[8],在辨识失效事件发生的可能性的同时,识别这些事件所带来后果的严重程度。风险定义为对不期望发生的结果的概率和其严重性乘积[8],表达式如下:

根据故障元件是否确定,可以将系统故障的风险评估[9-11]分成下述 2 种情况。
a.故障元件不确定。考虑可能发生的故障及后果,在给定或随机抽样的运行方式下,计算各种故障的风险指标,累计得到全局系统的平均风险指标,来表征系统的总体风险水平。计算流程如图1所示。

图1 全局风险指标评估流程图Fig.1 Flowchart of global risk index estimation
b.故障元件确定。针对某一指定故障元件,在给定或随机抽样的运行方式下,计算该故障的风险指标,得到的是系统在这一指定故障下的局部风险水平信息。计算流程如图2所示。
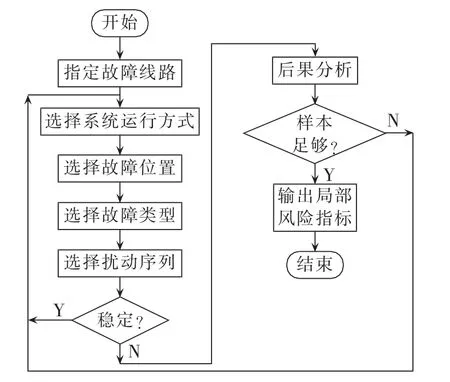
图2 局部风险指标评估流程Fig.2 Flowchart of local risk index estimation
全局风险指标考虑了系统中可能发生的所有故障,计算量较大,更适用于离线计算。而局部风险指标的计算量较之全局指标大为减小,更适用于在线计算。实际应用时,可综合考虑系统规模、运行方式变化情况和计算速度等因素予以选择。
2 重合时序灵敏度
将改变重合时序而引起的表征系统特征的指标变化量定义为该问题对重合时序的灵敏度。例如,衡量系统暂态稳定性的指标可选用暂态功角稳定裕度[5]和暂态电压安全裕度[7],也可采用临界切除时间。
据线路首、末端重合时暂态功角稳定裕度λMAh、λMAe,可得暂态功角稳定裕度对重合时序的灵敏度SMA:

暂态电压稳定裕度对重合时序的灵敏度SMV为:

将分别由线路首、末端重合时的暂态功角稳定临界切除时间记作tAch、tAce,暂态电压稳定临界切除时间记作tVch、tVce,则可由下式计算得到从时间裕度角度出发的暂态功角稳定对重合时序的灵敏度STA和暂态电压稳定对重合时序的灵敏度STV:

3 全局风险指标与重合时序灵敏度相结合的策略协调
3.1 基于时间裕度的暂态稳定风险指标
对电力系统暂态稳定影响较大的不确定性因素主要有系统运行方式(A)、故障发生的概率(B)、故障位置(C)、故障类型(D)和重合闸成功率(E)等,对各个因素的概率分布简述如下[8]。
a.系统运行方式。实际系统的典型运行方式通常考虑丰期大方式、丰期小方式、枯期大方式和枯期小方式4种,历史数据充分时,可通过统计确定其对应概率,否则,可按均匀分布进行计算第h种运行方式发生的概率为 P(Ah)。
b.故障发生的概率。线路发生故障的概率一般满足泊松分布,计算式如下:

其中,P(Bi)为第 i条线路发生故障的概率;λi为给定时间段内第i条线路发生故障的频率;nL为待分析的线路总数。
c.故障位置的概率。根据计算需要,将线路划分成M段,在第j段发生故障的概率为:

其中,lj为线路第j段的故障数。
d.故障类型的概率。计算暂态稳定时通常考虑的故障类型有单相接地、两相接地、三相短路和两相相间短路4类,分布情况可由历史数据统计得到,计算式如下:

其中,tk为第k种故障类型的数目。
e.重合闸不成功的概率。一般故障信息管理系统中不会记载重合闸的成功率,可由与成功率密切相关的故障原因概率来估算。统计分析结果显示,雷击跳闸的重合成功率在90%左右,而非雷击跳闸的重合成功率一般在50%,则重合闸不成功的概率可由下式计算:

其中,P(E)为重合闸失败概率;P(L)、P(N)为雷击、非雷击故障发生的概率;为雷击、非雷击故障下重合闸失败的条件概率。
结合上述A、B、C、D、E 5个方面不确定性因素,可以得到系统在第h种运行方式、第i条线路的第j段内发生第k种类型故障时重合闸不成功的概率:

故障临界切除时间是表征系统暂态稳定性的一个重要指标,它反映了故障对系统的影响程度。时间裕度定义为故障的临界切除时间与整定切除时间的差值[12],它可用以衡量故障的严重程度,裕度越大,系统的稳定性越好。结合式(12)计算出的故障概率与时间裕度定义第n个故障的风险指标绝对值RnA和相对值RnR如下:

其中,tnc为第n个故障下的临界切除时间(s);tns为第n个故障的整定切除时间(s)。
第n个故障的综合风险指标RGn定义为风险指标绝对值和相对值的平均值:

系统中待分析故障的总数记为nc,利用式(13)逐一计算得到各个故障的综合风险指标后,形成风险指标向量RG:

系统的全局风险指标[8]定义为:

其中,ω1、ω2为权重系数,ω1+ω2=1;‖RG‖1、‖RG‖∞为向量RG的1范数和∞范数。
3.2 暂态功角与电压稳定视角下的重合时序策略协调
3.2.1 基于时间裕度的暂态稳定性全局风险指标计算步骤
暂态稳定视角下的全局风险指标计算步骤如下:
a.计算预想故障集中各故障下线路首端重合时暂态功角与电压稳定的故障临界切除时间tncAh、tncVh;
b.计算预想故障集中各故障下线路末端重合时暂态功角与电压稳定的故障临界切除时间tcnAe、tncVe;
c.由式(13)计算首端重合时各个故障下的暂态功角和电压稳定综合风险指标RnGAh和RnGVh,并以此对各个故障进行排序;
d.由式(13)计算末端重合时各个故障下的暂态功角和电压稳定综合风险指标RGnAe和RGnVe,并以此对各个故障进行排序;
e.由式(14)计算首端重合时系统的全局暂态功角和电压安全风险指标RWAh和RWVh;
f.由式(14)计算末端重合时系统的全局暂态功角和电压安全风险指标RWAe和RWVe;
g.由式(15)、(16)计算重合时序改变对全局暂态功角和暂态电压风险指标的影响程度RWA和RWV。

3.2.2 重合时序策略协调
从提高系统暂态功角稳定性和暂态电压稳定性的角度提出的重合时序的整定方法,二者的整定思路是一致的。差异在于前者是对功角轨迹进行量化评估,通过2种重合时序下的暂态功角稳定裕度,得到优化的重合时序方案;而后者是对负荷节点的电压变化轨迹进行定量评估,比较2种重合时序下的暂态电压安全裕度后,给出重合时序方案。如果系统不能保持暂态功角稳定,必然也不能满足暂态电压稳定。即使系统能保持暂态功角稳定,但暂态电压稳定却不一定能够满足。
求得线路首、末端重合时的暂态电压安全裕度λMVh和λMVe和首、末端重合时的暂态功角稳定裕度λMAh和λMAe;或计算暂态功角稳定临界切除时间tAch、tAce和暂态电压稳定临界切除时间tVch、tVce。由于暂态功角稳定裕度和暂态电压安全裕度的内涵不同,不能直接比较,提出全局风险指标与重合时序灵敏度相结合的暂态功角、电压重合时序策略协调方案,计算流程如图3所示。监测到故障发生时,由式(2)或式(4)计算出暂态功角稳定性对重合时序的灵敏度,由式(3)或式(5)计算出暂态电压稳定性对重合时序的灵敏度,结合预先计算好的系统暂态功角、电压全局风险指标变化量RWA、RWV,考虑权重计算反映重合时序对暂态功角、电压稳定影响程度的综合指标CMA和CMV:

其中,ω3、ω4为全局风险指标变化量与重合时序灵敏度的权重,ω3+ω4=1。

图3 提高暂态功角和电压稳定的重合时序方案协调Fig.3 Coordination of reclose sequence strategies to enhance transient angle and voltage stability
通过比较综合指标CMA和CMV,选取较大者对应的重合时序方案作为协调方案。
暂态功角稳定临界切除时间和暂态电压稳定临界切除时间具有相同的量纲,在未获得系统全局风险指标时,结合暂态稳定裕度和临界切除时间,采用“失稳优先”原则的简化重合时序协调方案,见图4。

图4 TAS和TVS视角下重合时序策略的简化协调方案Fig.4 Simplified coordination scheme of reclose sequence strategies in view of TAS and TVS
首先判断2种重合时序下功角稳定裕度乘积的符号,若乘积为负,表明可通过改变重合时序将系统由失稳变为稳定,则选择可提高系统暂态功角稳定性的重合时序方案。若乘积为正,继而判断2种重合时序下暂态电压安全裕度的符号,若为负,则选择可提高系统暂态电压稳定性的方案。功角和电压裕度的乘积均为正时,分别计算基于时间裕度的重合时序灵敏度STA和STV,比较二者的大小:若STA较大,则表明重合时序对功角稳定性的影响较大,选取提高暂态功角稳定性的方案;若STV较大,则选取提高暂态电压稳定性的方案。
4 局部风险指标与重合时序灵敏度相结合的策略协调
局部风险指标与全局风险指标的差别在于,前者针对给定的单一故障进行计算,而后者要考虑系统中可能出现的故障。应用于在线计算[13-15]时,一旦检测到故障发生,由保护装置提供的信号可确定故障线路和类型,系统对应的运行方式亦可确定,即系统运行方式(A)、故障发生的概率(B)、故障类型(D)均已成为确定性因素,若能获得由测距装置提供的故障距离,则故障位置(C)亦可确定。此时需考虑的不确定性因素主要有重合闸成功率(E)。则对于给定故障重合闸不成功的概率为:

4.1 基于时间裕度的暂态稳定性局部风险指标计算步骤
暂态稳定视角下的局部风险指标计算步骤如下:
a.确定系统运行方式、故障位置、故障类型等信息;
b.计算指定故障下线路首端重合时的暂态功角与电压稳定的故障临界切除时间tcAh和tcVh;
c.计算指定故障下线路末端重合时的暂态功角与电压稳定的故障临界切除时间tcAe和tcVe;
d.由式(13)计算首端重合时的暂态功角和电压稳定综合风险指标RGAh和RGVh;
e.由式(13)计算末端重合时的暂态功角和电压稳定综合风险指标RGAe和RGVe;
f.计算重合时序改变对全局暂态稳定和暂态电压风险指标的影响程度RGA和RGV。
4.2 重合时序策略协调
基于局部风险指标和灵敏度的重合时序暂稳协调方案如图5所示。

图5 基于局部风险指标和灵敏度的重合时序暂稳协调Fig.5 Coordination of reclose sequence strategies for transient stabiltity based on local risk index and sensitivity
5 仿真验证
3机9节点系统如图6所示,系统数据示于表1—4,功率基准值为 100 MV·A,表中电阻、电抗、导纳皆为标幺值。以该系统为例,分别仿真计算三相重合时序对暂态功角、电压稳定性的稳定裕度指标,进而分别计算全局风险指标、局部风险指标和重合时序灵敏度相结合的重合时序协调方案。
表4中,τj为发电机的惯性时间常数;x′d为直轴暂态电抗;x′q为交流暂态电抗;xd为直轴不饱和同步电抗;xq为交轴不饱和同步电抗;τ′d0为直轴暂态开路时间常数;τ′q0为交轴暂态开路时间常数;xL为定子漏抗;x″d为d轴次暂态电抗;x″q为q轴次暂态电抗;τ″d0为d轴次暂态时间常数;τ″q0为q轴次暂态时间常数。

图6 3机9节点系统Fig.6 3-generator 9-bus system

表1 3机9节点系统节点参数Tab.1 Node parameters of 3-generator 9-bus system

表2 3机9节点系统线路参数Tab.2 Line parameters of 3-generator 9-bus system

表3 3机9节点系统变压器参数Tab.3 Transfomer parameters of 3-generator 9-bus system

表4 3机9节点系统发电机参数Tab.4 Generator parameters of 3-generator 9-bus system
5.1 基于全局风险指标与重合时序灵敏度的协调
系统在不同运行方式下发电机出力和负荷水平如表5所示。在各运行方式下进行线路首端三相永久故障扫描计算,0 s线路首端故障,0.1 s线路首端断路器跳闸,0.12 s线路末端断路器跳闸,0.8 s先合闸侧重合,0.9 s重合侧再次跳闸。得到各故障下线路首、末端重合时的暂态功角稳定和暂态电压稳定的临界切除时间,以运行方式1为例,线路首、末端重合时的暂态功角、电压稳定临界切除时间tAc和tVc示于表6和表7。

表5 运行方式信息Tab.5 Information of operating mode

表6 运行方式1暂态功角稳定临界切除时间Tab.6 CCT of transient angle stability in operating mode 1

表7 运行方式1暂态电压稳定临界切除时间Tab.7 CCT of transient voltage stability in operating mode 1
故障原因采用文献[8] 中的统计数据,雷击故障率为82.51%,非雷击故障率为17.49%,则由式(9)计算重合闸不成功的概率为:

以系统中分别发生故障5和故障12为例,权重系数ω1、ω2均取 0.5,由式(14)算得各运行方式下暂态功角稳定和暂态电压稳定的系统全局风险指标R后,由式(15)、(16)计算其变化量。由稳定裕度信息计算故障5和故障12的灵敏度S,由式(17)、(18)计算综合评价指标 C,ω3、ω4均取 0.5,计算结果见表8。

表8 各运行方式综合评价指标Tab.8 Comprehensive estimation index for different operating modes
对比综合评价指标可以发现,发生故障5时,在运行方式1和4下,输出的是提高暂态电压稳定的重合时序方案,即由线路首端首先重合,而在运行方式2、3、5、6下,输出的是提高暂态功角稳定的重合时序方案,即由线路末端首先重合。发生故障12时,在考察的6种运行方式下,均得到由提高暂态功角稳定的重合时序方案,即由线路首端首先重合。
以运行方式1下发生故障5为例,暂态功角和电压稳定的综合指标分别为0.1339和0.1356,比较可知,应采用提高系统暂态电压稳定的重合方案,即由线路首端首先重合。综合评价指标与权重系数ω3的变化关系如图7所示。暂态功角稳定和暂态电压稳定的综合指标均随权重系数ω3的增大而增大,二者曲线交于权重系数为0.5383处。权重小于该值时,输出的是提高暂态电压稳定的重合时序方案;若大于该值,则选择提高暂态功角稳定的方案。

图7 综合指标与权重系数变化关系Fig.7 Relationship between comprehensive index and weight coefficient
5.2 基于局部风险指标与重合时序灵敏度的协调
以运行方式1下的故障5和故障12为例,由式(13)计算故障下的系统暂态功角稳定和电压稳定的风险指标R后,计算其变化量。由稳定裕度信息计算灵敏度S,考虑权重系数计算综合评价指标C,权重系数均取0.5时的计算结果见表9和表10。故障5下暂态功角和电压稳定的综合指标分别为0.1938和0.1194,比较可知,应采用提高系统暂态功角稳定的重合方案,即由线路末端首先重合。故障12下暂态功角和电压稳定的综合指标分别为0.083 4和0.0411,比较可知,应采用提高系统暂态功角稳定的重合方案,即由线路首端首先重合。

表9 故障5局部风险指标与灵敏度结合的评价指标Tab.9 Estimation index integrating local risk index with sensitivity for fault 5

表10 故障12局部风险指标与灵敏度结合的评价指标Tab.10 Estimation index integrating local risk index with sensitivity for fault 12
6 结论
分别从暂态功角和电压稳定视角下提出的重合时序整定策略,角度和适用场景有所不同与侧重。2个视角下得到的重合时序策略冲突时,需进行协调。本文提出的风险指标与重合时序灵敏度相结合的重合时序协调方法,可以有效协调这种冲突。
3机9节点系统中的计算表明:结合全局风险指标与重合时序灵敏度的协调结果部分故障下与运行方式有关。分别采用全局、局部风险指标与重合时序灵敏度结合的方法对同一故障的协调结果有可能不一致,实际应用时,可综合考虑系统规模、运行方式变化情况和计算速度等因素予以选择。

