兆瓦级全功率风电并网变流器功率组件设计

杨 捷，金新民，吴学智，梁小广，宋高升，尹靖元

（1.北京交通大学 电气工程学院，北京 100044；2.三菱电机机电（上海）有限公司，上海 200245）

0 引言

风能不仅可以缓解能源危机，还可以抑制环境的恶化，因此受到世界各国的广泛关注[1-5]。全球风电产业2012年新增风电装机容量达44800 MW，使全球累计风电装机容量达到282500 MW。在全球经济的大背景下，风电成为可再生能源发电技术的首选[6]。变流器是风电机组的重要组成部分，目前主流变流器分为双馈变流器和全功率变流器。全功率变流器能实现风机与电网的完全隔离，因此能够实现更大范围的最大功率点跟踪，故障穿越能力也更强。如今，全功率变流器已经成为大功率风电变流器发展的主要趋势[7-11]。

与小功率变流器一体化结构设计不同，鉴于散热、维护等因素，大功率兆瓦级变流器主要采用模块化功率组件结构设计。功率组件是兆瓦级全功率变流器的重要组成部分，功率组件设计水平直接决定了变流器的性能。影响功率组件可靠性和寿命的主要因素包括功率器件的温升与直流侧滤波电容的温升。器件损耗估算方法一直是变流器设计的难点问题。已有很多文献对器件功率损耗进行研究。文献[12-17] 对器件每个阶段的工作状态进行了深入的分析，模拟器件特性搭建了器件的物理模型以及损耗模型，这种方法精确度高，但是要求用户清楚器件内部结构和工作特性，且模型参数确定过程非常复杂，不容易被应用到实际工程中；指数方法[18-20]是将损耗表示成交流电流指数幂形式，计算速度比物理模型快，但计算前需要大量测试数据；文献[20-22] 充分利用器件手册数据，采取线性化方法计算器件损耗，使用方便简单，但只适用于交流电流纹波小的情况。针对上述问题，本文在考虑交流电流纹波的基础上，提出一种高精度功率器件损耗计算方法，该方法只需器件手册即可实现损耗估算，适用于实际工程应用。

传统直流电容选型方法只从直流电压稳定性能与跟随性能[23-24]出发，并未考虑电容的纹波电流。实际上直流电容温升与直流侧纹波电流密切相关，纹波电流过高将导致电容发热甚至损坏，影响功率组件的可靠性。文献[25-28] 已对直流侧纹波电流进行了深入的研究，但是没有考虑功率组件间连接的杂散参数对各组件直流电容纹波的影响，并不适用于采用功率组件结构的兆瓦级全功率风电并网变流器。本文在考虑功率组件间杂散参数对直流电容纹波电流的影响后，提出一种分析电容纹波的简化方法，为直流电容的选型提供了更全面的依据。

最后，为验证所提方法适用于兆瓦级全功率风电并网变流器的功率组件设计，本文据此设计了包含功率器件、散热器、直流电容、电流传感器等器件的1 MW标准功率组件，并对所设计的功率组件进行了全面的测试。测试结果表明所提计算方法的正确性，可满足兆瓦级风电变流器的设计要求。

1 器件的损耗计算

1.1 器件损耗分析及计算方法

精确估算器件损耗对散热系统的设计具有重要的指导意义。由于文献[20-22] 提出的线性方法简单易用，被广泛应用到工程中。这种方法计算时认为每个开关周期交流电流不变，但实际由于开关频率次纹波的存在，开通关断时的估算值与实际值存在误差，交流电流纹波越大，估算精度越低。因此本文在拟合过程中将考虑交流电流纹波对器件开关损耗的影响，提出一种精度较高的损耗估算方法。

器件S运行时功率损耗主要包括通态损耗Pon-s和开关损耗Psw2个部分。

1.1.1 通态损耗Pon-s

利用器件手册中器件端压降US与电流IS关系曲线，可以将器件电压、电流进行线性拟合，表达式为：

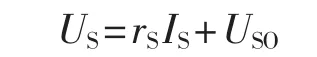
其中，rS、USO分别为器件正向导通电阻和擎住电压。

设器件S在一个基波周期T0内导通区间为[t1，t2] ，式（1）为器件通态损耗的表达式。

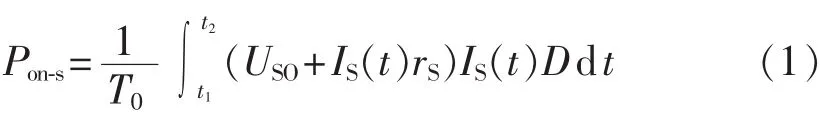
其中，占空比D是关于调制比M和时间t的函数。

1.1.2 开关损耗Psw

器件手册给出了特定条件下的单个脉冲损失的能量，包括IGBT开通损耗的能量Eon.nor、IGBT关断损耗的能量Eoff.nor以及二极管的反向恢复损耗的能量Err.nor。在结温和驱动电阻相同的情况下，开关损耗的能量与器件电压、电流基本呈线性关系，因此可以得到单个脉冲损耗能量的一般表达如式（2）所示。

其中，Ion、Ioff、Irr分别为 IGBT 开通、关断和二极管反向恢复时刻对应的电流值，Udc为直流电压，Inor、Udcnor分别为特定条件下对应的电流、电压。若运行时器件开关频率为fs，在导通区间对单个脉冲损失的能量进行积分，即可得到开关损耗的表达如式（3）所示。

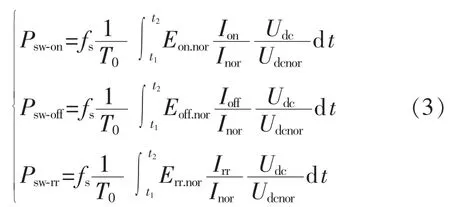
1.1.3 器件损耗计算方法

如上文所述，传统算法认为每个开关周期Tsw的导通区间内交流电流不变，即开通电流Ion与关断电流Ioff相等，这种假设将导致估算精度在交流纹波大时明显降低。每个开关周期内，器件电流的平均值应符合下式：

其中，Ip为交流电流峰值。

考虑开关频率次电流纹波的存在，则每个开关周期导通区间[0，DTsw] 内器件交流电流的表达式如式（4）所示。

其中，L为滤波电感值，占空比D与调制方式有关。本文采用SPWM方法，此时IGBT、二极管占空比的表达式如式（5）所示[29]。

将式（4）、（5）代入式（1）、（3）可以推导出 IGBT和二极管通态损耗、开关损耗分别如式（6）、（7）所示。

IGBT损耗PI、二极管损耗PD以及器件总损耗Ptotal如式（8）所示。

其中，n为每个模块所含IGBT或二极管个数。

1.2 1 MW功率组件器件损耗算例

1MW风电变流器的功率组件技术参数如下：直流电压为1000 V，交流电压为690V，交流电流为1000 A。

本文采用的功率器件CM1800DY-34S属于桥臂模块，即n=2，电感L实际中取50 μH。利用CM-1800DY-34S器件手册①Mitsubishi Electric.CM1800DY-34S application note.2010.，得到在Udc=1000 V、器件电流 IS=1800 A、驱动电阻Rg=1ω、结温Tj=125℃的条件下，计算损耗所需要的器件参数为：Uceo=1.5 V，UD=1.1 V，rIGBT=0.66 mΩ，rD=0.64 mΩ，Eon=1050 mJ，Eoff=450 mJ，Err=350 m J。其中结温 Tj=125°C，与第 4节实验情况相符。

功率组件主要运行于网侧变流器、机侧变流器2种工况下。不同功率因数下，功率器件损耗差别很大，需进行详细计算分析。将上述CM1800DY-34S的技术指标和技术参数代入式（6）、（7）可得到IGBT损耗、二极管损耗、总损耗与功率因数F、调制比M的关系，关系曲线见图1。从图中可知，功率因数F=1时（网侧变流器）IGBT功率损耗最高；功率因数F=-1时（机侧变流器）二极管功率损耗最高；器件总损耗最高可达4704 W，因此按照5000 W来设计水冷散热器。

2 直流电容电流纹波分析

2.1 直流电容电流纹波理论分析

直流电容吸收PWM变流器产生的高频纹波电流，纹波电流与电容温升有密切关联。若直流电容选择不当，纹波电流大于电容额定电流，将造成电容温升过高甚至损坏。

传统直流纹波电流计算是利用三相PWM开关矢量推导出直流侧电流的平均值Idc和有效值Irms的表达式，继而可以得到纹波电流有效值Irip表达式如式（9）所示[26]。

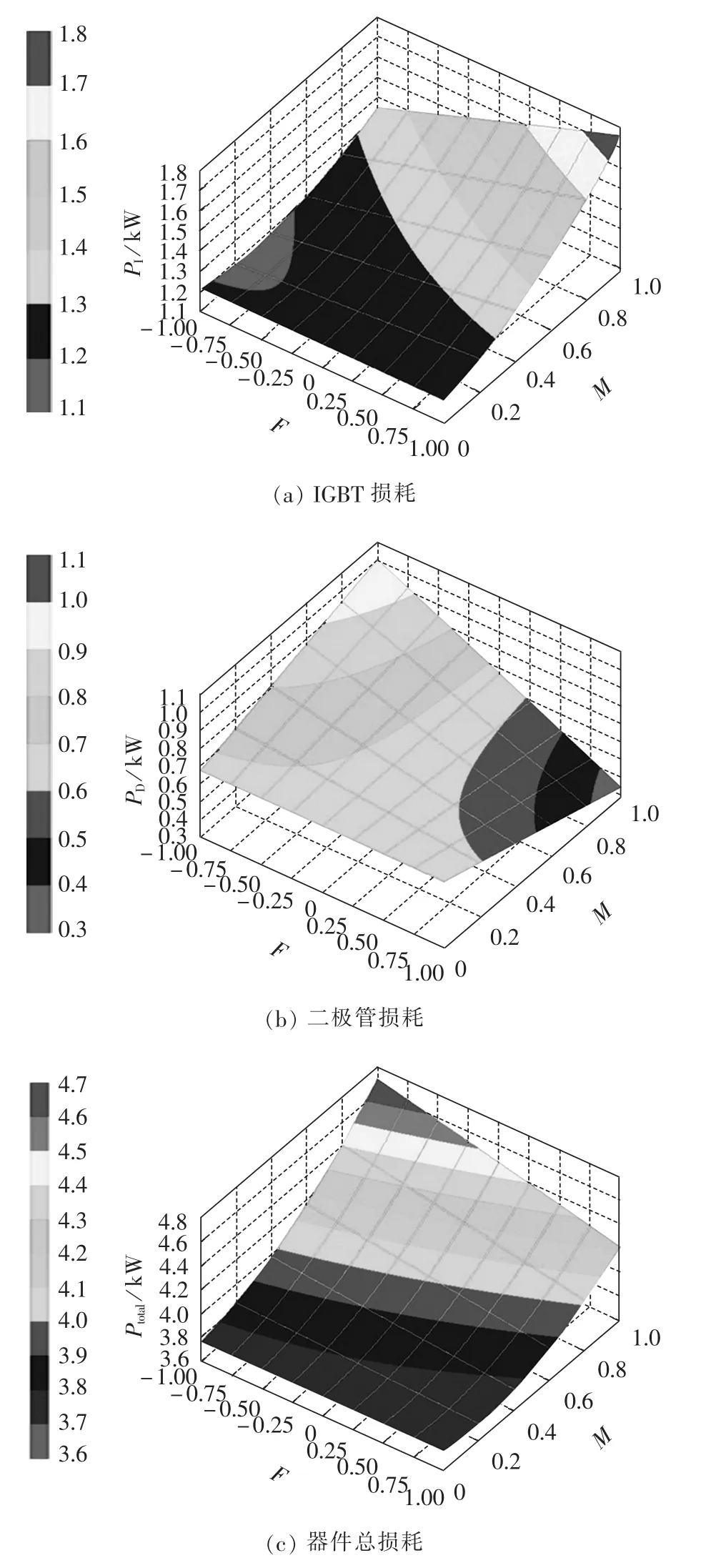
图1 器件损耗、调制比M和功率因数F关系曲线Fig.1 Relationship curves among power loss，modulation ratio and power factor

其中，Iorms为输出交流电流有效值，每相功率组件的直流电容平均分配总纹波电流Irip的1／3。

然而兆瓦级全功率风电并网变流器由功率组件方式构成，目前设计基本都采用低ESR薄膜电容构成直流单元，组件之间通过铜排连接。薄膜电容与铜排电感之间构成LC谐振回路，导致直流电容的电流纹波显著增加。考虑连接杂散参数后，变流器的等效电路如图2所示。

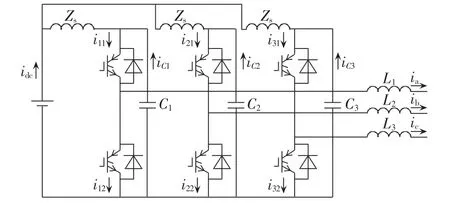
图2 含杂散参数的变流器电路Fig.2 Converter circuit with parasitic parameters

将每相桥臂视为PWM谐波电流源，假设三相杂散参数相同，变流器等效简化模型如图3所示。

图3 变流器等效简化模型Fig.3 Equivalent and simplified model of converter

ihx（x=a，b，c）为每相桥臂的谐波电流源；Rs为杂散电阻，主要是由复合母排的电阻与电容的ESR组成；Ls为杂散电感，一般在10～100 nH之间。从简化模型可以看出，该电路为具有初始储能值的二阶电路，若杂散电阻小于临界阻尼，即，则产生谐振。但是实际设计中，为了限制铜排的损耗，通常杂散电阻的阻值远小于临界阻尼，容易导致电容纹波电流显著增加。

根据叠加原理可得到每相直流电容纹波有效值为：

2.2 1 MW功率组件直流电容纹波算例

直流电容纹波有效值是关于输出电流Iorms、杂散电感Ls、杂散电阻Rs、直流电容Cdc、调制比M以及功率因数cos θ的函数，解析表达式非常复杂，本文给出了数值计算结果，并将其绘制成曲面图，如图4所示。从图中可以看出纹波电流随着杂散电感的增大而增加，电容越小发生振荡的可能性就越大。因此，在设计功率组件时，应尽量减小线路中的杂散电感，并增大直流电容以降低电路的临界阻尼。

图4 电容纹波电流、杂散电感、直流电容关系曲线Fig.4 Relationship curves among capacitor ripple current，parasitic inductance and DC-link capacitor

本文在设计功率组件时，采用复合母排连接以降低杂散电感，复合母排的杂散电感大约为30 nH。为避开纹波电流过高的区域，结合图4，直流电容容值应大于4.3 mF。综合直流电压稳定性能和跟踪性能考虑，本文采用10个470 μF／1100 V／50 A的薄膜电容并联作为直流单元，此时对应每相直流纹波电流为427 A，小于电容额定电流。

3 功率组件的实现

3.1 功率组件原理

功率组件原理图如图5所示。功率组件主要功能是实现直流-交流转换，其输入直流电压经直流侧滤波电容滤波后，给开关器件相桥臂提供直流电能；通过控制器件动作，将输入直流电能转换成电压和频率可调节的输出交流电能。

图5 功率组件原理图Fig.5 Schematic diagram of power stack

3.2 结构设计

为了减小系统体积，降低杂散参数，减少加工难度，兆瓦级功率组件设计应采用标准化模块结构，将功率器件、散热系统、传感器等元件紧凑地集成于高功率密度的功率组件中。按此设计的1 MW功率组件的结构如图6所示。其中，1为水冷板，2为CM-1800DY-34S，3为转接板，4为测温电阻，5为吸收电容，6为复合母排，7为电流传感器，8为直流电容。

图6 1 MW功率组件结构图Fig.6 Structure of 1 MW power stack

4 实验验证

为验证所提方法正确性，本文分别进行了简化的组件测试实验和后期的整机实验。

4.1 组件测试

组件测试是在整机实验之前，搭建H桥电路提前检验功率组件的稳定性和可靠性，图7为组件测试实验的原理图。

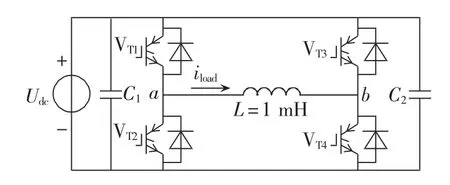
图7 组件测试实验原理图Fig.7 Schematic diagram of stack test

利用所提算法可知，iload=1200 A时H桥电路可模拟功率组件在最大损耗4704 W下的运行情况，此时各器件损耗为：PI=1 678 W，PD=722 W，Ptotal=4 800 W。图8为组件测试实验波形，在极限进水温度50℃条件下，热稳定时主要元件的温度为：IGBT 96.9℃；二极管92.3℃；直流电容35.8℃；进水温度50℃；出水温度57.7℃；散热器最高温度87.3℃。

图8 组件测试实验波形Fig.8 Experimental waveforms of stack test

4.2 整机实验

整机实验为机侧变流器、网侧变流器之间进行的1 MW功率互馈实验，原理图如图9所示。图10为整机实验的实验波形，图10（a）中，Ubc为网侧电压，iN、iG分别为网侧和机侧电流。在极限进水温度50℃条件下，热稳定时主要元件的温度如表1所示。

图9 1 MW互馈实验平台Fig.9 Platform of 1 MW mutual-feeding experiment

图10 1 MW互馈实验波形Fig.10 Experimental waveforms of 1 MW mutual-feeding experiment

表1 1 MW互馈实验元件温度Tab.1 Device temperature of 1 MW mutual-feeding experiment

4.3 损耗估算方法验证

对比4.1节中的器件损耗、元件温度和表1可知，进水温度相同的条件下，2个实验出水温度及散热器最高温度相同，说明组件测试的总损耗与整机实验基本吻合。该器件壳-散热器热阻为0.0062 K／W，结合图1、4.1节中的器件损耗、元件温度和表1可以将传统方法和本文方法进行精度对比，如表2所示。从表2中可知，由于组件实验和整机实验滤波电感值不同，传统方法的误差存在较大差异，说明交流电流纹波对传统方法精度影响较大；与传统方法相比，本文所提考虑交流电流纹波的方法明显提高了损耗估算精度。另外，IGBT与二极管壳-芯片热阻分别为0.0213 K／W，0.0366 K／W，结合表2中损耗的实测值计算出IGBT与二极管的结温都在125℃附近，以上损耗估算的设定条件与实验基本相符。

表2 损耗实测值与估算值的对比Tab.2 Comparison between measured and estimated losses

4.4 电容纹波电流分析方法验证

图10（b）中电容纹波实测值为38.4 A，本文方法和传统方法估算的电容纹波分别为42.7 A、18.2 A。据对比显示，采用本文所提电容纹波分析模型得到的电流值与实测值吻合较好，误差比传统方法小，证明了本文所提考虑杂散参数的电容纹波分析方法的有效性。

5 结论

本文针对影响兆瓦级全功率风电并网变流器功率组件运行可靠性的两大问题，提出了精度更高的器件损耗估算方法和电容纹波电流分析方法，并用于1 MW功率组件的设计，组件测试和整机实验验证了所提方法有较好的精确性，适用于兆瓦级功率组件设计。

a.详细分析了器件损耗估算方法的推导过程，指出传统估算方法精度不高的主要原因在于没有考虑交流电流纹波的影响，并进行了改进。

b.损耗估算方法可以计算各种工况下IGBT和二极管的损耗，只需用到器件手册数据，公式简单，具有较强的工程应用价值。

c.直流电容选型时应考虑电容纹波这一重要因素，而传统选型方法只关注直流电压的稳定性和跟随性。

d.传统方法认为电容纹波只与调制比、功率因数、输出电流有关，本文指出电容纹波还受杂散参数、电容本身参数的影响较大。采用本文方法可对电容纹波进行较精确的分析，为兆瓦级功率组件直流电容选型提供重要依据。