负荷模型简化辨识及在河南电网的仿真应用

王景钢，孙建华，付红军

（河南电力调度控制中心，河南 郑州 450052）

0 引言

电力综合负荷是电力系统的重要组成部分，其中感应电动机负荷是最主要的动态成分。为了得到更加符合实际的负荷模型，电网运行人员希望通过实测方法建立可信的模型。总体测辨法就是通过现场实测的电力负荷特性数据，利用系统辨识具体负荷群的等值感应电动机负荷模型。文献[1] 提出了一种综合负荷模型，经现场实测数据验证，该模型泛化能力较强，且曲线拟合精度更高。但由于在结构中加入了感应电动机模型，该模型有14个待辨识参数，使得该负荷模型的待辨识参数很多，负荷模型的结构变得更加复杂，在工程应用上非常不方便。因此，有必要对综合负荷模型的结构以及参数进行简化。

本文从简化负荷模型辨识入手，结合电网实际扰动仿真、暂态故障曲线Prony分析以及电网小扰动分析等电网实例，使用综稳程序PSASP对模型简化前后进行了仿真验证。

1 综合负荷模型感应电动机模型结构

三阶感应电动机部分待辨识的参数：Rs、Xs、Xm、Rr、Xr、H、A、B，它们都是电动机容量基值下的标幺值；ZIP 模型部分待辨识的参数：kPP、kPZ、kQP、kQZ。除以上12个参数外，为了将所有模型参数标幺化还定义了参数Kpm和Mlf，Kpm用来分配初始有功功率，Mlf为额定初始负荷率系数。综合负荷模型结构见图1。

图1 综合负荷模型结构Fig1 Structure of composite load model

设负荷总的初始有功、无功功率分别为P0、Q0，感应电动机的初始有功功率为P′0，则定义Kpm为：

定义Mlf为：

其中，SMB为感应电动机的额定容量。

若 U0、P′0、Rs、Xs、Xm、Rr、Xr、H、A、B（皆为在电动机容量基值下的标幺值）均为已知，那么有：

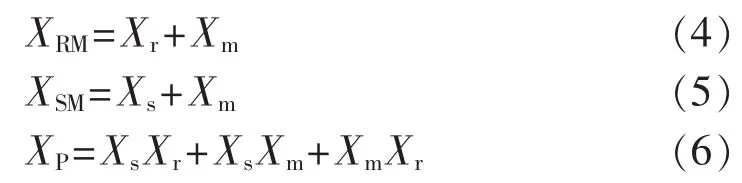
可得：

所以有：

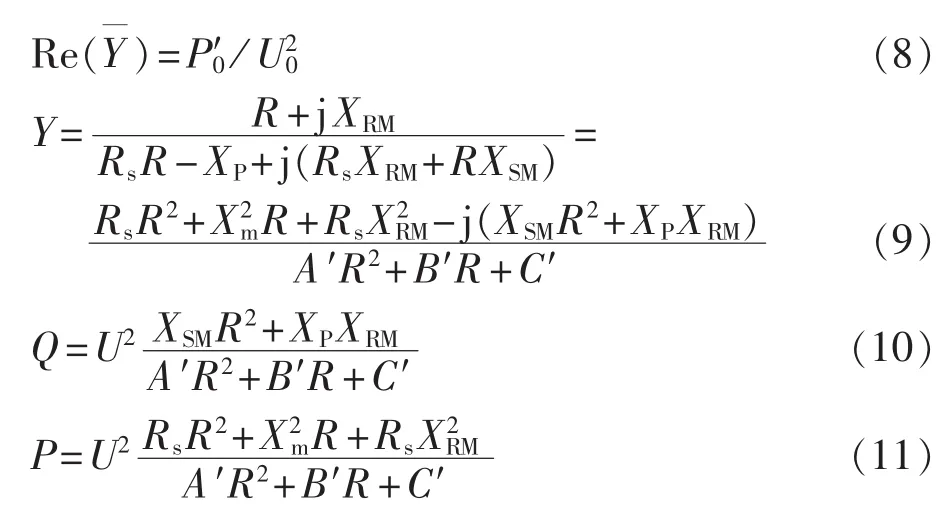
其中，XRM为转子电抗；XSM为定子电抗；XP无物理意义，为参与计算代入值；R为转子电阻。

由此得到Q、P随电压U变化的函数Q=F（U）和P=F（U），如果做出一个包括凹陷和凸变的电压扰动序列，就可以得到一个相应的无功和有功响应序列。

2 电动机参数灵敏度分析

表1给出了进行辨识所采用的综合负荷模型的14个参数值，以下摄动分析都基于这14个参数值进行。

摄动方法为每次固定其他参数值，仅对1个参数进行10%的扰动变化，观察电动机参数的变化对系统功率的影响。图2、3为摄动感应电动机负荷各参数，在电压发生凹陷及凸变的同一时刻，取该时刻的无功、有功响应的数值，用参数变化比例作为横坐标，依次描点所得的无功响应曲线。由此可直观地看出，在电压发生变化时Kpm、Mlf对系统动态影响很大。

表1 综合负荷模型的参数值Tab.1 Parameters of composite load model

图2 无功响应曲线Fig.2 Response curves of reactive power

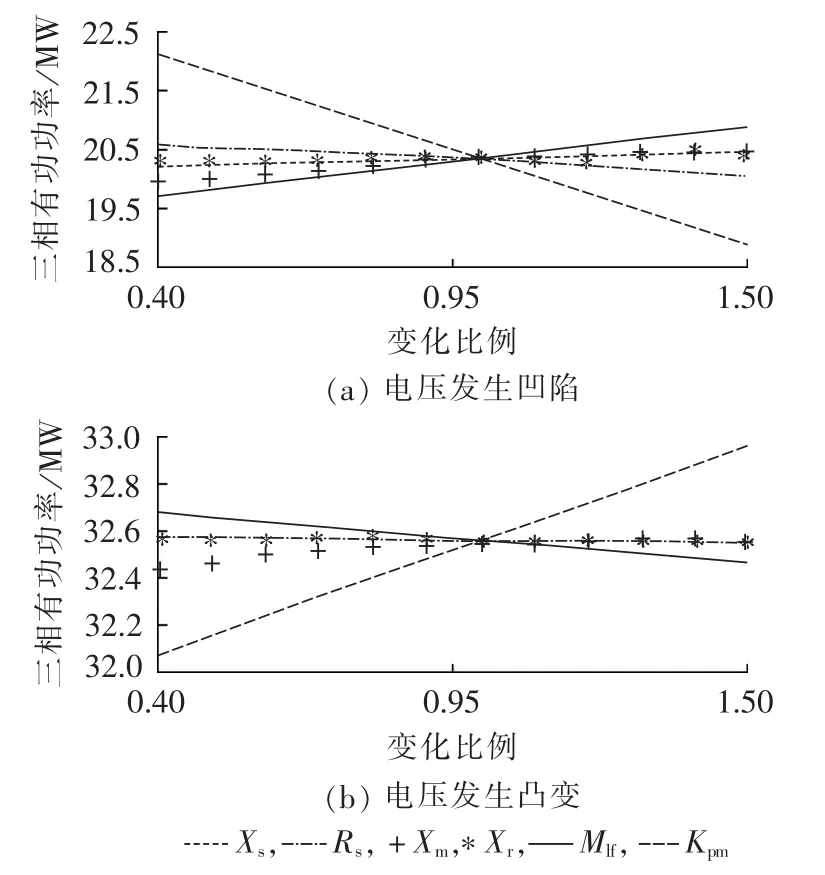
图3 有功响应曲线Fig.3 Response curves of active power

在综合负荷模型中，Mlf与电动机的基准容量密切相关。电动机的比例一定，即Kpm一定时，Mlf越小，综合负荷模型中等值电动机的容量就越大，电动机特性对系统动态的影响就越大。当Kpm越大或者Mlf越小时，电动机负荷起到“缓冲器”的作用，减小电压波动下负荷响应对系统的冲击。

3 简化辨识误差分析及实例仿真

3.1 误差分析

在参数简化辨识之后，需用误差指标对辨识结果进行校验，本文对此从整体上给一个误差指标，定义为误差能量指标Ee：

其中，ysimp（i）为简化辨识变量序列，ydeta（i）为详细辨识变量序列，ystab为详细辨识数据序列扰动前稳态值，N为实测变量与仿真变量个数。ysimp、ydeta、ystab从简化辨识数据变量和详细辨识数据变量的局部动态特性上刻画了二者的差异，可从有功曲线和无功曲线分别统计误差指标，总体指标为二者之和。

式（12）为详细辨识数据和简化辨识数据的偏差能量相对于详细辨识数据变量扰动能量的比值，反映了一定扰动强度下，仿真误差整体值的大小，是一个宏观的误差指标。当该值接近零时，详细辨识与简化辨识模型的结构完全吻合；该值越大，误差越大。

大量建模实验表明，Et＜10×10-3为可接受的误差范围。通过比较发现，简化模型能够较准确地反映负荷特性。为了说明模型对负荷特性的描述能力，对于某变电站2010年测得的357条数据，分别利用简化和详细辨识模型进行建模，从统计学的角度，上述误差分析指标给出了357条数据的平均误差、最大误差、最小误差以及误差的方差如表2所示。这里简化的负荷模型中Rs的取值为0.35。从误差的平均值和误差的方差都可以看出，简化后的综合负荷模型在描述测点无功、有功变化方面与详细辨识的模型精度相差不大。从目前对已测得的负荷曲线的拟合程度来看，该负荷模型结构能够反映已记录的配电网的有功功率和无功功率随电压变化的动态特性。

表2 2010年全年数据统计误差Tab.2 Statistical error of 2010’s annual data

3.2 实例仿真

图4 简化及详细模型仿真与实测曲线比较Fig.4 Comparison between measured curve and curve simulated with simplified or detailed model

图4为某次电网波动后使用PSASP进行仿真分析的结果，可见简化辨识前后曲线拟合效果基本一致。简化辨识与详细辨识的误差为：功角曲线7.47×10-4，母线电压曲线6.18×10-4，仿真结果非常接近。

图5和表3、4为某条500 kV线路发生三相接地故障时详细辨识模型与简化模型系统功角曲线及Prony分析结果，本文只示出作用较强的振荡模式的Prony分析结果，其中振荡模式2为主导振荡模式。由Prony分析可见，系统振荡频率分别为0.369575Hz、0.380 481 Hz，阻尼比分别为3.79% 和3.61%，2种负荷模型的电网动态稳定性分析结果一致。

图6、7为使用详细辨识模型与简化模型，进行系统小扰动分析后得到的河南对四川振荡模式的对比模态图，采用2种负荷模型下分析的振荡频率分别为0.379869 Hz和0.38035 Hz，阻尼比均在9.2%左右，简化辨识负荷模型在大电网仿真工程应用上具有和详细模型仿真辨识一致的拟合效果。

图5 同一扰动下详细模型功角曲线及Prony分析结果Fig.5 Power angle curve of detailed model and result of Prony analysis for same disturbance

表3 同一扰动下详细模型的Prony分析Tab.3 Prony analysis of detailed model for same disturbance

表4 同一扰动下简化模型的Prony分析Tab.4 Prony analysis of simplified model for same disturbance

图6 详细模型的模态图Fig.6 Modal chart of detailed model

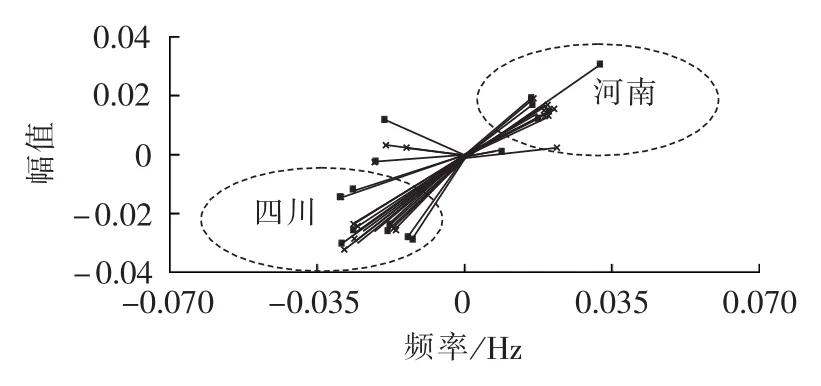
图7 简化模型的模态图Fig.7 Modal chart of simplified model

4 结论

本文针对从现场安装的负荷记录仪所得的实测数据，使用负荷建模系统程序，进行了感应电动机负荷模型参数解析灵敏度分析，并利用负荷辨识软件以及PSASP加以仿真验证，简化参数模型和详细参数辨识模型的仿真结果非常接近，简化辨识参数的工作是可行的，用参数灵敏度分析的方法指导简化辨识的思路也是实测负荷模型实用化的重要方法之一。

简化辨识后的负荷模型可以节省大量参数辨识的时间，其泛化能力较强、曲线拟合精度较高，具有工程推广的价值。在下一步工作中，将在电网日常方式分析及年度方式计算中进一步推进和改进负荷模型参数简化辨识在实际工作中的应用。