适用于宽带电力线通信的OFDM信噪比估计方法

梁 栋，张保会，牛东文，付科源，郝治国

（西安交通大学 电力设备电气绝缘国家重点实验室，陕西 西安 710049）

0 引言

高级量测体系AMI（Advanced Metering Infrastructure）与智能电网（smart grid）和智能家居（smart home）的快速发展对高速可靠的电力线数据通信提出了更高的要求。自适应正交频分复用AOFDM（Adaptive Orthogonal Frequency Division Multiplexing）技术为带宽受限的电力线信道提供了高效的数据通信解决方案。AOFDM中最为关键的参数就是准确的信噪比SNR（Signal to Noise Ratio）。自适应算法如比特能量分配算法、turbo码解码以及信道均衡等算法都要求有准确有效的信噪比估计参数。

信噪比估计算法一般分为2种：第1种是数据辅助（DA）的估计方法（data-aided estimator），该方法使用OFDM系统的同步帧或者导频来完成估计；第2种是盲估计（blind estimator）算法，该算法建立在有用信号和噪声的统计特性基础上，采用盲估计算法的系统效率更高，然而其估计性能不如数据辅助的估计算法。上述2种算法适用于不同场合的通信系统。

单载波通信系统在加性高斯白噪声信道（AWGN）下有许多高效的信噪比估计算法，比如最小均方误差（MMSE）算法、二阶四阶矩（M2M4）算法和最大似然（ML）算法等。这些算法在AWGN信道下大多可以直接推广到多载波的OFDM系统中。然而对于多径电力线信道而言，频率选择性衰减、严重的电力线背景噪声和脉冲噪声使得以上算法的估计性能严重下降。对于OFDM系统的信噪比估计问题已经引起很多的学者关注［4-7］。文献［6］针对无线信道中的MIMO-OFDM系统提出了一种信噪比估计算法，算法通过2段相同的前导序列来估计噪声功率和信号功率，估计值在信噪比低于一定门槛时趋近于-3 dB。文献［7］为中压电力线信道提出了一种基于相位的信噪比估计算法，同样在信噪比较低时估计效果不甚理想。本文提出一种适用于电力线信道的信噪比估计算法。该算法通过使用重复结构同步训练序列中的虚拟子载波或者保护边带的虚载波，可以灵活地进行数据辅助估计或者盲估计，使整个系统高效地完成自适应通信。由于虚载波中只含有噪声信息，所以在频域计算接收信号的二阶矩就能很容易地推导出系统的平均信噪比。算法最多使用1个同步训练序列，而且计算复杂度比经典的信噪比估计算法要低。

1 系统模型

1.1 OFDM系统接收机模型

本节首先介绍了基于电力线通信的OFDM系统模型。假设系统已经完成了完美的时间和频率同步，并且循环前缀（cyclic prefix）足够长，以抵消信道时延扩展使得系统没有码间干扰（ISI）和载波间干扰（ICI）。图1所示为自适应OFDM通过电力线信道的系统框图。

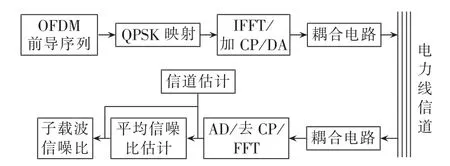
图1 信噪比估计系统框图Fig.1 Block diagram of SNR estimation system

本文自适应OFDM系统中使用重复结构的训练序列作为前导码来完成同步和信道估计等计算。序列是由N个单位幅度的QPSK数据符号cm（k）组成，可以记作 Cm= ［cm（1），cm（2），…，cm（k），…，cm（N）］，其中 N 为逆傅里叶（IFFT）运算的长度，m（=0，1）表示第 m 个 OFDM 符号，k（=1，2，…，N）代表第k个子载波。本文以4段相等的训练序列为例，序列满足：

由于没有ICI和ISI，并且循环前缀比信道冲击响应要长，在接收机完成了同步运算后，频域的接收信号可以表示为：

其中，nm（k）为服从零均值方差为的复高斯分布；S为每个子信道上接收信号的功率；W为噪声的功率；Hm（k）为电力线信道的频率响应，由式（3）给出。

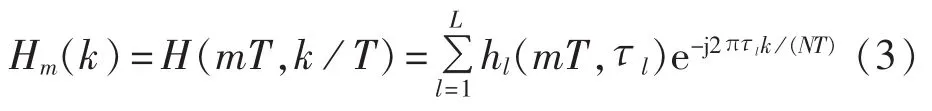
其中，hl（mT，τl）为第 m 个 OFDM 前导符号在信道第l径上的增益系数，满足T 为OFDM前导符号的持续时间；L为电力线信道多径的总径数。

1.2 电力线信道测量与建模

要得出可信的计算与仿真结果，电力线信道的准确测量和建模十分重要。本文采用了基于传输线理论的自下而上的建模方法［8-10］，低压电力线信道网络拓扑、电缆和负载参数在典型的大学办公室环境实测得到。根据文献［8］的方法，电力线网络拓扑被分割成若干个基本单元，每个基本单元的传输函数可以由式（4）计算。

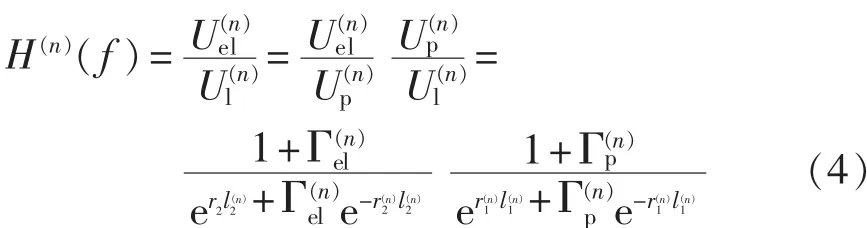
图2和图3分别给出5条有不同传输函数的低压电力线信道的幅频特性图和相频特性图，频率范围为 10 kHz～40 MHz。

噪声建模方面，低压电网的噪声主要包括［1］：有色背景噪声、周期或非周期性的脉冲噪声和由空间耦合过来的窄带干扰。

实测中有色背景噪声变换相对缓慢，所以自回归（AR）模型被用作背景噪声建模；脉冲噪声则使用服从泊松分布的模型。办公室环境下24 h实测电力线噪声见图4。

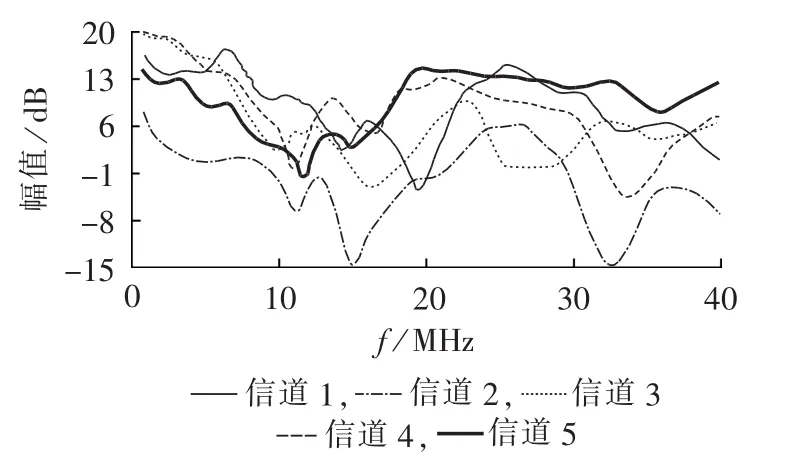
图2 电力线信道幅频响应Fig.2 Amplitude-frequency response of power line channel

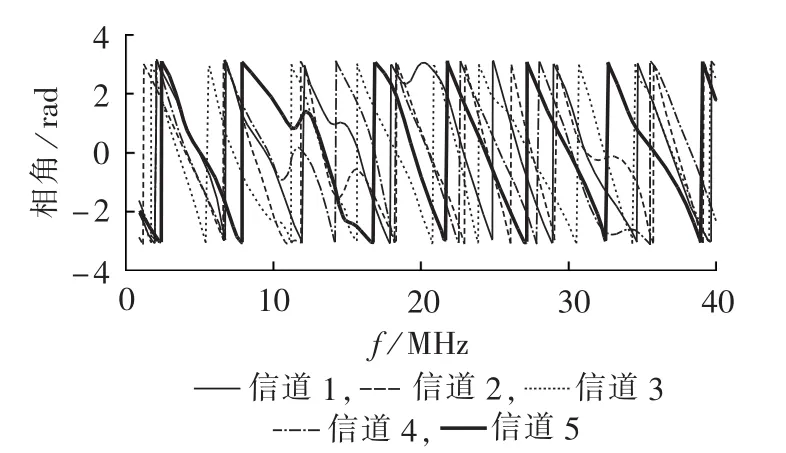
图3 电力线信道相频响应Fig.3 Phase-frequency response of power line channel

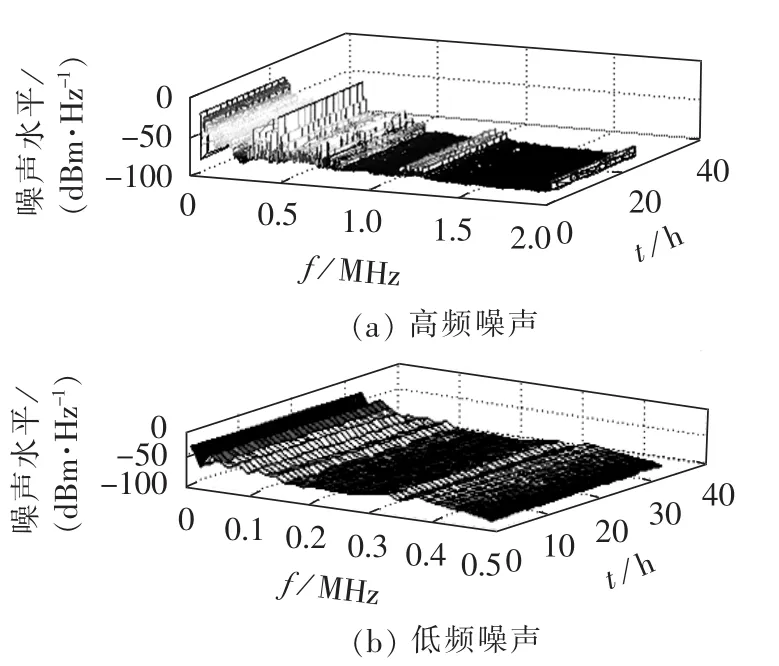
图4 24 h实测电力线噪声Fig.4 Measured power line noise for 24 hours

2 OFDM信噪比估计算法

基于上述OFDM系统模型和电力线信道模型，对接收端第m个OFDM符号的信噪比估计可以表示为：

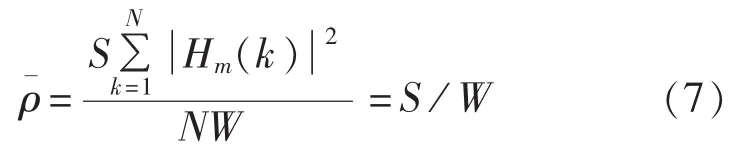
而每个子载波上的信噪比为：

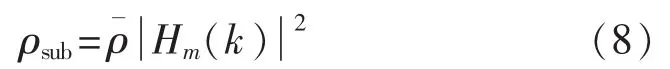
最小均方误差（MMSE）的信噪比估计算法是以估计值误差与信道频率响应估计的正交性为基础，其表达式为：

其中，Y（n）、C（n）分别为接收信号和原始发送序列的幅值，N为序列的长度，“*”表示共轭。

文献［6］为采用2段相等结构同步训练序列的MIMO-OFDM提出一种新的信噪比估计算法，此方法可以扩展到SISO-OFDM系统中，算法可表示为：

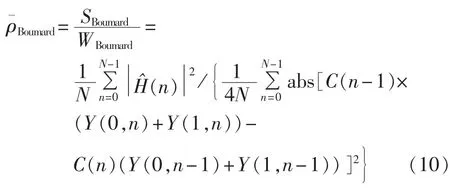
其中，Y（k，n）为接收信号中第k+1个符号的第n个抽样的幅值；abs［·］表示取绝对值。

盲信噪比估计中经典的算法有M2M4算法，算法对接收信号分别做二阶矩和四阶矩并化简，该算法可以表示为：

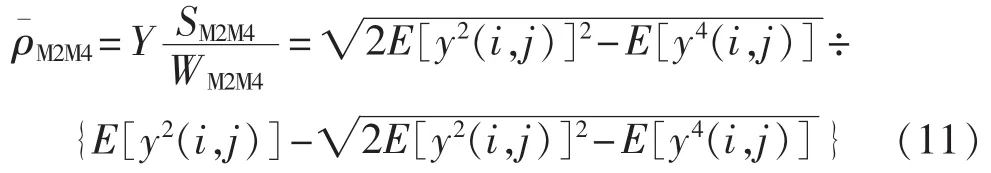
其中，y（i，j）为第 i个接收符号的第 j个抽样值。

本文提出算法用于数据辅助估计时采用系统的同步训练序列。本文使用的同步训练序列在时域上为4段相等的结构，这样在频域上2个装载了数据的相邻子载波间有3个虚拟的子载波。对于有N个子载波的OFDM系统，虚拟子载波如下：

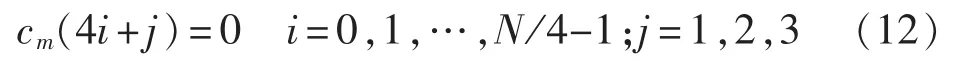
而其余的子载波 cm（4i）（i=0，1，…，N／4-1）为QPSK映射后的复数。这样接收信号的二阶矩可以写为：

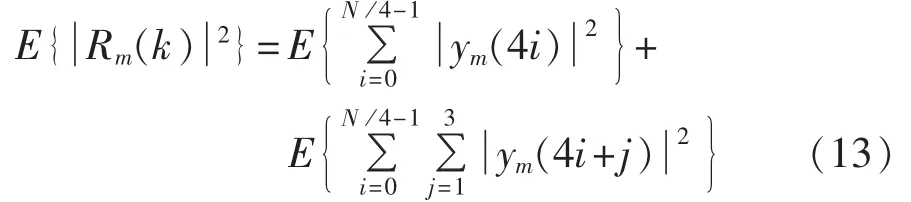
等式右边的第1项可以化为：

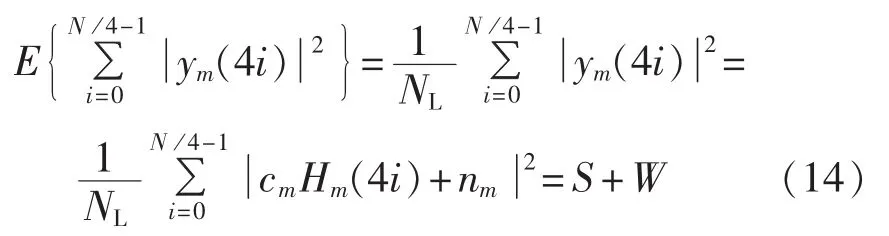
其中，NL为数据子载波的数目。

第2项是虚拟子载波二阶矩的期望值：

所以基于虚拟子载波的OFDM平均信噪比估计可以写作：

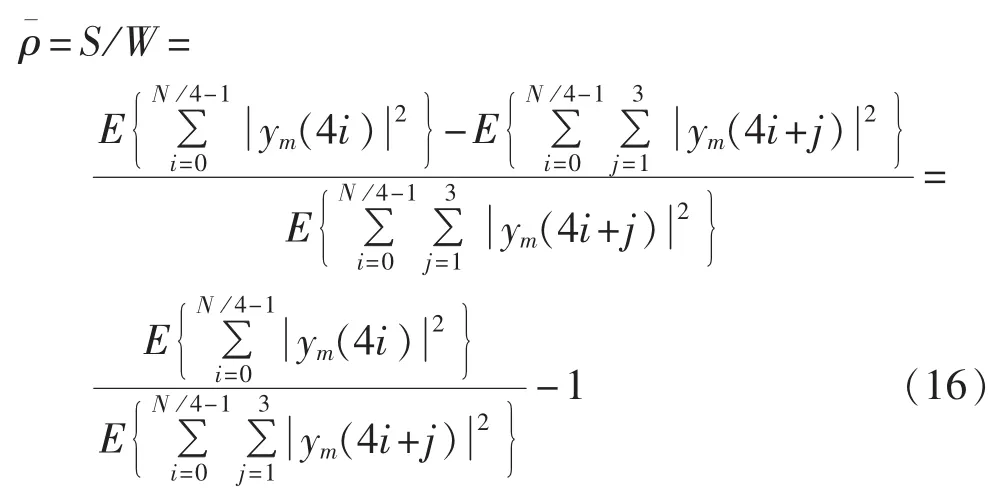
同理，在OFDM频域首尾两端的保护虚拟子载波可以用来进行信噪比的盲估计。假设系统频域cm（k）（k=0，1，…，t-1）和 cm（k）（k=N-t+1，…，N）为虚拟子载波，而其他载波为QPSK映射的数据。这样可以由任意一帧不含有训练序列或导频的OFDM信号估计得到信噪比：

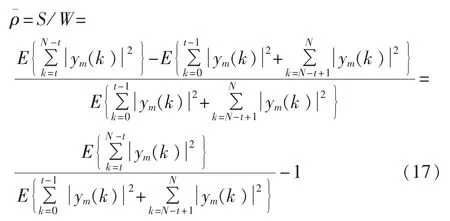
每个子载波的信噪比可以由平均信噪比ρ¯和信道系数得到：

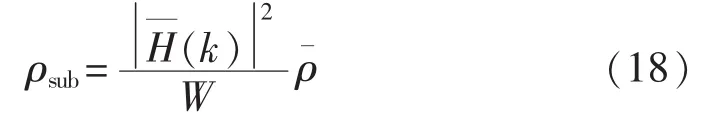
从式（16）、（17）可以看出，本文算法只需要计算接收端训练序列时域各点的能量，然后求比值，只需要N次乘法运算，比经典信噪比估计算法式（9）—（11）更加高效，因此更加适用于实际载波系统的硬件实现。同时由等式（14）、（18）可以看出本文算法的估计精度是受虚拟子载波的数目以及信道系统的估计精度影响。

3 仿真验证

信噪比估计算法的仿真采用了蒙特卡洛仿真方法，进行10 000次的仿真计算。本文算法用作数据辅助算法时与经典的MMSE算法以及Boumard算法进行比较，用作盲估计时与经典的M2M4算法做对比。系统参数如下：每个OFDM符号采用1 024个子载波，循环前缀84个采样长度；前导帧包含2个训练序列，其中本文算法利用第1个训练序列而Boumard算法使用全部的2个训练序列；在盲估计的系统中同样使用1 024个子载波的OFDM符号，其中首尾共有102个子载波为虚拟子载波。

信噪比估计的性能分析对比在AWGN信道（信道1）和基于实测数据的低压电力线信道（信道2）中展开；算法的对比结果采用归一化均方误差值（NMSE）来对比：

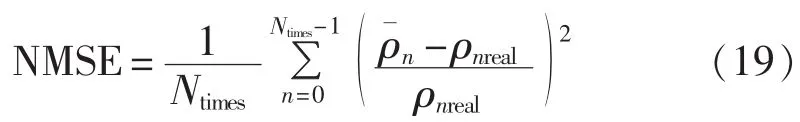
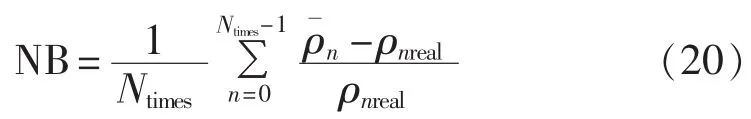
对于每个子载波的归一化均方误差为：

图5所示为本文算法与Boumard算法、MMSE算法通过实测电力线信道的平均信噪比均值在数据辅助模式下的对比。仿真结果可见本文算法与Boumard算法在实际信噪比大于-5 dB的区间估计性能均好于MMSE算法，但在实际信噪比低于-5 dB的情况下，本文算法具有比其他2种算法更好的估计性能。在实际信噪比趋于-∞时，Boumard算法的估计值趋于-3 dB。

图6和图7所示为不同数据辅助算法的归一化均方误差和归一化偏差对比图。可见在实际信噪比较高的情况下本文算法与Boumard算法有近似的估计精度，而在实际信噪比较低的情况下本文算法的误差要小于另外2种算法，在-20 dB下算法的归一化偏差也很小。

图8和图9显示了不同算法在盲估计模式时的性能对比。图8所示为信噪比的估计均值对比，图9为归一化均方误差对比。盲估计可以用在信噪比估计的跟踪模式或者其他对精度要求较低的场合。本文算法与M2M4算法在1个OFDM符号内均使用102个虚拟子载波，算法在实测电力线信道中实现。可见在大多数情况下，本文算法的估计精度要高于经典的M2M4算法。

图10所示为各算法在不同的信道下的归一化均方误差的对比。同其他算法相比本文算法在电力线信道和AWGN信道下均显示出较好的估计性能，更加接近克拉美罗界。

图5 不同数据辅助算法的平均信噪比估计均值Fig.5 Mean of SNR estimated by different DA algorithms

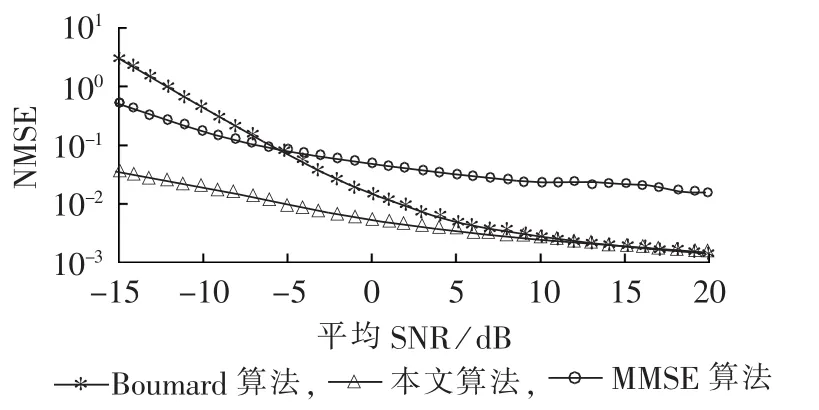
图6 不同数据辅助算法的信噪比估计归一化均方误差Fig.6 NMSE of SNR estimated by different DA algorithms

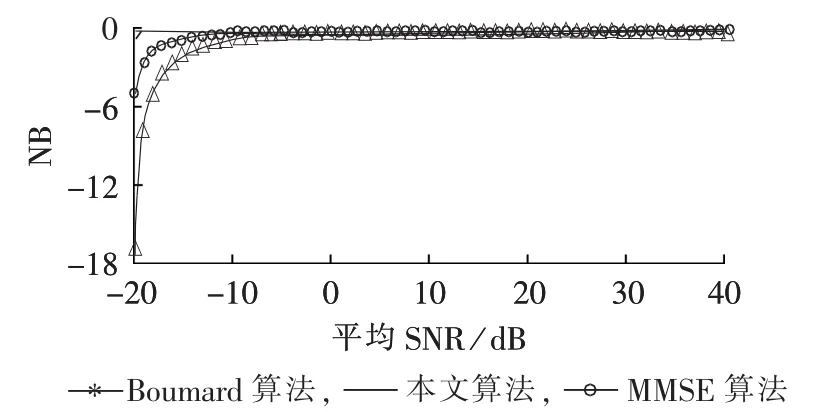
图7 不同数据辅助算法的信噪比估计归一化偏差Fig.7 NB of SNR estimated by different DA algorithms

图8 不同盲估计算法的平均信噪比估计均值Fig.8 Mean of SNR estimated by different blind estimation algorithms

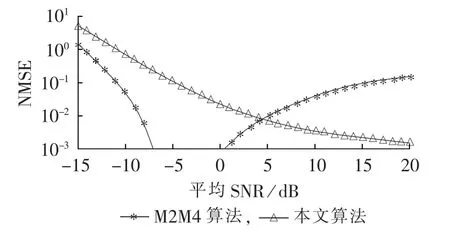
图9 不同盲估计算法的信噪比估计归一化均方误差Fig.9 NMSE of SNR estimated by different blind estimation algorithms

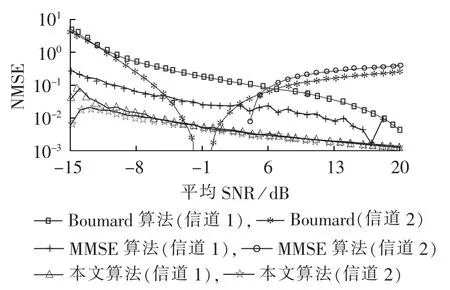
图10 信道1和信道2的信噪比估计归一化均方误差Fig.10 NMSE of estimated SNR of channel 1 and channel 2

4 结论

自适应OFDM为带宽受限的电力线通信提供了高效的频带利用率和更高速的比特率。准确并且灵活的信噪比估计算法是实现自适应OFDM的前提和基础。研究适用于电力线信道特点的信噪比估计算法对改善宽带电力线的通信质量有非常重要的意义。

本文针对电力线信道下自适应OFDM系统中的信噪比估计问题，提出一种基于虚载波的算法。该算法使用频域中的虚拟子载波信息，通过计算接收信号的二阶矩来完成信噪比的推导，可以灵活运用于需要数据辅助估计和盲估计的情况。计算机仿真结果表明本文算法在实测电力线信道下有较高的估计精度，同时算法复杂度相对较低，是一种适用于实际系统的信噪比估计方法。