一种基于谱修正数字脉压旁瓣抑制的改进方法*
张云雷 龚 诚 卢建斌 席泽敏
(1.海军工程大学电子工程学院 武汉 430033)(2.海军司令部 北京 100032)
1 引言
线性调频信号经过匹配滤波后的归一化第一旁瓣约-13.2dB,显然这样高的距离旁瓣在检测中会引起虚警,或是将所在距离单元的主瓣淹没,实际脉压中均需要设计旁瓣抑制。通常,脉压的旁瓣特性用峰值旁瓣比(PSLR)和积分旁瓣比(ISLR)来衡量,前者指最高旁瓣能量和主瓣能量之比,后者指副瓣能量和主瓣能量之比,一般用分贝数表示。
在气象雷达中应用脉冲压缩体制可以获得很多常规体制雷达不能达到的性能[1],但气象目标对距离旁瓣特性提出了更高的要求。由于气象目标往往有很大的动态范围,并分布在多个连续的距离单元中。如果不进行旁瓣抑制,大的峰值旁瓣会掩盖小目标,而大的积分旁瓣使临近距离单元的能量进入当前检测单元,从而影响当前距离单元的检测。文献[2]提出气象雷达若应用脉冲压缩体制,为了精确测量分布式目标的反射率和速度,对50m/s以内的气象目标,要求峰值旁瓣在-40dB以下;测量降雨的气象雷达为了检测地杂波中的雨水目标,通常要求PSLR在-60dB以下[3~4]。而采用一般加窗抑制旁瓣,只能达到-40dB的PSLR,远不能达到测高超低旁瓣的要求。
时宽带宽(BT)积是脉压信号的一个重要参数,决定了脉压前后的脉宽比。一般来说,由于菲涅尔起伏,小BT积信号脉压效果往往较差,为了得到和大BT积信号相似的性能,文献[5~6]提出的频谱修正的方法,通过对信号频谱进行矩形化修正,可以降低距离旁瓣。通过对该算法分析发现,如果选择合适的窗函数可使得PLSR达到-60dB的效果,但往往带来很大的主瓣展宽和信噪比损失。本文通过分析加窗的机理,提出了改变窗函数频域加权的带宽的方法,在可以接受的主瓣展宽和信噪比损失条件下,得到很低的峰值旁瓣。
2 窗函数加权局限性
加窗进行距离旁瓣抑制是脉压雷达的常用方法。加窗分为时域加窗和频域加窗,当时BT积较大时,两者的效果趋向于相同[7]。由于匹配滤波往往设计成加权系数保存,采用频域加窗处理能够不增加匹配滤波的工作量,所以频域加窗应用更加普遍。
这里对频域加窗的窗函数加权降低旁瓣的过程进行分析。常见的窗函数为升余弦窗,频域加窗时的表达为[8]

当k=0.08,n=2时就是常用的海明窗;当k=0.5,n=2时为汉宁窗。
当信号BT积较大时,信号频谱在过渡带的菲涅尔起伏较小,近似为矩形,此时可以表示为
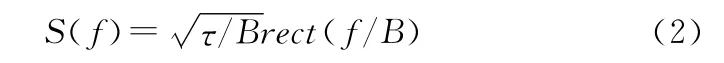
脉压结果可以用信号通过加权网络的输出表示,其中网络的传输系数见式(1),所以脉压输出可以表示为

上式中g1(t)、g2(t)和g3(t)分别为三个谐波分量,表示为
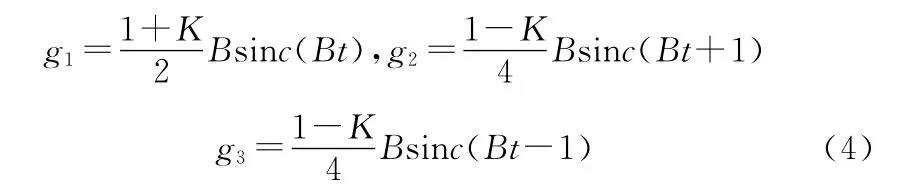
故窗函数的频谱可以看做谐波分量搬移后的加权和,图1给出了海明窗的三个谐波分量降低旁瓣的过程。

图1 海明窗函数频谱分量示意图
从式(3)可以看出,窗函数加权降低旁瓣的过程可以从频谱搬移上来解释。频域上加窗(点乘)相当于时域上对sinc函数进行搬移并加权求和,如果式(1)中选择合适的K值,使得时域上信号不同谐波的峰值和谷值叠加相消,就能达到降低旁瓣的效果。
常见窗函数加窗后脉压性能如表1所示[8]。可以看出不同窗函数的旁瓣性能不同,随着旁瓣的降低,信噪比损失和主瓣展宽也变大。需要指出的是,表1给出的结果是当BT>200时得到的,当信号的BT<100时,信号频谱并不能等效于矩形谱,加窗输出脉冲还不能达到表1的性能。

表1 常见窗函数的脉压性能表
3 谱修正算法及改进
从上面讨论可知,当线性调频信号的BT积较小时,此时信号频谱和矩形谱差别较大,文献[6]通过对信号频谱修正,可以得到较好的旁瓣效果,称为谱修正算法。假设信号的频谱为S(f),频域窗函数为W(f),*表示共轭操作,则修正后的匹配滤波器表示为
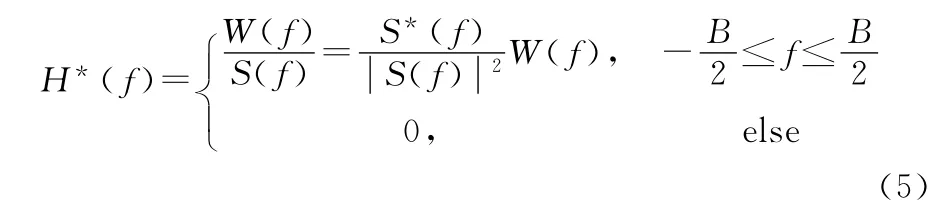
经过该滤波器后信号输出为
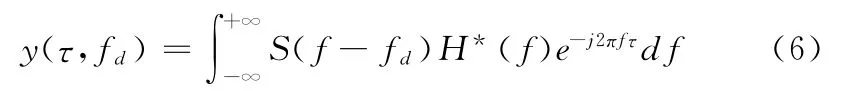
假定信号的频谱为矩形谱,见式(2),当fd=0时,则有:
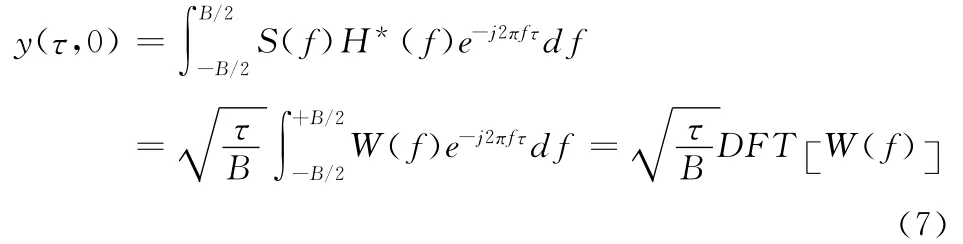
从式(7)可以看出,脉压结果可以表示为窗函数的傅里叶变换,故可通过选择频谱特性满足旁瓣要求的窗函数W(f)来实现超低旁瓣,如布莱克曼窗、切比雪夫窗等[9]。由于部分窗函数的旁瓣可控,如切比雪夫窗,理论上可以得到任意低的脉压输出,但仿真表明,超低旁瓣脉压的结果对应的主瓣展宽和信噪比损失也很大,见表2。应用中一般需满足主瓣展宽不大于1.5,信噪比损失小于1dB,可以看出,在上述要求下超低旁瓣性能条件下的其他性能很难得到满足。
图2给出了采用2倍信号带宽采样的频域加窗的示意图。矩形虚线框代表了信号带宽,不规则波形为信号频谱,信号频谱主要能量分布在矩形框内,由于频谱存在泄露[10],在整个采样频带内都有能量分布。-60dB的切比雪夫窗函数为点划线表示,该窗函数在信号带宽内的频谱形状很窄,所以对信号的频谱的削减很厉害,导致较大的信噪比损失和主瓣展宽。为了保留频带外信号能量,减小能量损失,这里引入频带展宽因子α,将窗函数的加窗频带扩展,见双划线所示,此时α=1.5。

图2 基于频谱修正的加窗对信号频谱影响
采用扩展窗函数加窗频带方式的参考函数见式(8)所示,通过扩展频带,减少了频带内信号能量的损失,且对频带外泄漏的信号能量也部分保留;同时由于等效带宽的增加,减小了主瓣展宽。须注意这里的信号采样频率须大于信号带宽。

注意,如果采取增大带宽后截断窗的方法,同样可减少滤波能量损失,但对窗函数进行截断处理会恶化距离旁瓣性能,这是因为截断会改变窗函数机理。本文所提出的扩展频带方法是对加窗的信号带宽增大,而窗函数形状不变,可得到较好的效果,但系统必须保证大于信号采样带宽。
4 算法仿真
条件设置:频线性调频信号,带宽10MHz,采样频率20MHz,脉冲宽度为20μs,信噪比60dB,采用Blackman窗函数加权。仿真过程如下:
Step1:生成线性调频信号;
Step2:进行FFT变换;
Step3:选择窗函数,生成频域滤波器系数;
Step4:频域加窗;
Step5:进行IFFT变换得到脉压输出;
Step6:统计输出脉压性能。
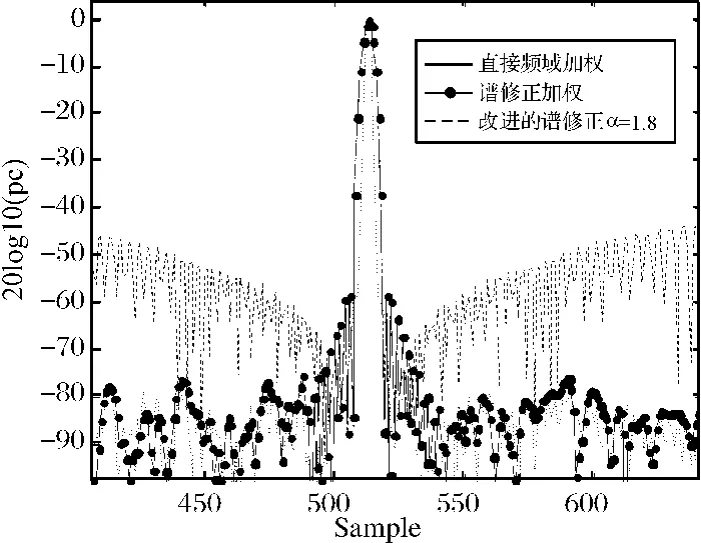
图3 不同频域加权脉压效果
图3给出了采用Blackman频域脉压结果,将频域直接加权输出和经过频谱修正、改进的谱修正算法的脉压结果画在一起,可以看出,谱修正算法和改进后的谱修正算法均能够有效地抑制旁瓣,但改进算法的主瓣展宽更小。表2给出了几种窗函数采用谱修正(SMA)和本文算法(α-SMA)算法的频域加权脉压输出性能,其中α=1.4。可以看出,后者明显优于前者。

表2 SMA和α-SMA脉压输出性能(α=1.4)
不同α的脉压性能是不同的。一般来说,α越大信号能量保留的越多,信噪比损失越小。但当α增大到一定程度时,扩大α所带来的信号能量收益小于进入噪声或杂波的能量时,信噪比的损失会变大,所以存在一个使得信噪比损失最小α值,该值和回波噪声功率有关。

图4 α-SMA算法脉压性能随α的变化
图4给出了采用Blackman窗函数脉压性能随展宽因子α的仿真,仿真条件见图3条件按设置。可以看出,随着α的增大,主瓣展宽减小,逐渐逼近于理想值1;而信噪比损失则存在极小值,这是因为信噪比损失存在一个对α的折中选择,如果限定最大信噪比,则存在最优的一个α值,而不同窗函数对应的最优值应该不同。表3给出了在信噪比-60dB条件下,不同窗函数在满足D<1.5时的最小α值。由于回波信号存在着各种畸变,包括动目标存在多普勒频移,故不能准确得到和发射的信号完全相同的频谱,由于修正的信号频谱和矩形谱存在较大差距,所以谱整形算法的旁瓣特性就会恶化,解决的办法一方面是放松对加窗整形的限制,使整形后的频谱不完全是窗函数而允许有一定的波动,从而提高脉压算法的鲁棒性;另一方面是对回波的畸变进行补偿。

表3 不同窗函数的α选择
5 结语
针对气象雷达应用脉冲压缩体制所需的超低旁瓣技术,本文通过改变加窗频带来改进频谱整形算法,在保证主瓣展宽和信噪比损失满足一定条件下,实现了一种并不增大运算量的超低旁瓣。仿真表明该方法能有效地解决旁瓣性能和分辨率的矛盾,可以应用于气象雷达中超低旁瓣设计。但必须满足的前提是此时的采样带宽须大于信号带宽,性能的提升是以硬件资源耗费为前提的。针对该算法的应用,本文进一步讨论了加宽因子的选择。由于对信号频谱进行修正的算法的旁瓣特性对信号畸变很敏感,所以需要重点解决算法鲁棒性的问题,这是下一步工作要研究的方向。
[1]Merrill I.Skolnlk.Radar handbook(Second Edition)[M].McGraw-Hill,c1990.
[2]Keeler R J,Hwang C A.Pulse compression for weather radar[C]//Radar Conference,Record of the IEEE 1995International,8-11May 1995:529-535.
[3]LARVOR J P.Digital pulse compression with low range sidelobes[J].Thomson–CSF/SDC,France:391-394.
[4]H.D.Griffiths,Ultra-Low Range Sidelobe Pulse Compression for Satellite-Borne Rain Radar[C]//Record of the 1993IEEE National Radar Conference,1993:28-33,20-22.
[5]吕幼新,向敬成,陈辅新.降低线性调频脉冲压缩信号旁瓣的方法[J].电子科技大学学报,1993,22(4):344-349.
[6]杨斌,武剑辉,向敬成.谱修正数字旁瓣抑制滤波器设计[J].系统工程与电子技术,2000,22(9):90-94.
[7]贺知明,黄巍,向敬成.数字脉压时域与频域处理方法的对比研究[J].电子科技大学学报,2002,32(2):120-124.
[8]向敬成,张明友.雷达系统[M].北京:电子工业出版社,2001,5.
[9]邹鲲,袁俊泉,龚享铱.MATLAB 6.x信号处理[M].北京:清华大学出版社,2002,5.
[10]程佩青.数字信号处理[M].第二版.北京:清华大学出版社,2001,8.

