大规模机器学习问题研究*
罗 霖
(中国人民解放军73232部队 舟山 316200)
1 引言
近年来,随着数据采集手段的飞速发展以及数据来源的日益丰富,尤其是互联网的大规模使用,我们所能获得的数据规模已经从十年前的数万、数十万到今天的动辄上千万、甚至是数亿,知识量成“爆炸式”增长,如文本分类数据库达到107样本个数,109样本维数。如何学习和处理这些大规模海量数据是当前值得关注而又亟需解决的问题。
目前,机器学习(Machine Learning)已经被公认是处理和学习这些数据最为有效的手段之一。将机器学习问题的求解归结为优化问题是当前机器学习界主流的做法。实际上,优化理论已经成为机器学习研究的核心内容之一,可以用经验风险最小化、最大似然、最大熵和最小描述长度等方法来表示,它是机器学习算法设计的根本依据。批处理(Batch)方法是优化理论早期的算法形式,如梯度下降法、(拟)牛顿法和内点法等,其每一步迭代都要遍历所有的样本信息甚至需要处理海森(Hesse)矩阵。如果处理规模较小的数据,可以直接用经典的批处理优化方法很容易对其求解,但是如果面临的是大规模海量数据,整个求解过程就发生了重大转变。以文本分类的数据库为例(规模为107个数,109维数),光存储数据本身所需要的内存空间为107×109×4Byte=4×107GB,当前64位计算机的内存总量也就是264Byte=16GB,即便全部拿来存储数据,其容量还是杯水车薪,更不要说去处理和分析数据。虽然这些年来计算机硬件也相应地有着快速发展,但仍跟不上数据集规模增大所带来的计算需求爆炸式增长的步伐。
因此,在实际应用中,对于大规模问题的学习算法的研究就是非常必要和迫切的。本文以大规模机器学习问题的研究为主线,围绕坐标优化和在线优化算法,综述近几年来求解大规模机器学习问题的相关理论和研究进展。
2 机器学习若干问题介绍
机器学习最初的研究动机是为了让计算机系统具有人的学习能力[1~2],以便实现人工智能。上世纪四、五十年代兴起的神经网络和感知机算法在一些特殊领域取得了良好效果[3],但Vapnik指出“这些理论成果并没有对一般的学习理论带来多大贡献[4]。”自上世纪九十年代以来,具有坚实理论基础和良好应用效果的 SVM[5]、adaBoost[6]等算法吸引了人们极大的兴趣,统计机器学习理论从此也进入了蓬勃发展期。
自1995年以来,机器学习理论经历了“间隔”和“损失函数”两个重要的发展阶段。在损失函数具有贝叶斯一致性的前提条件下[7],大多数机器学习问题都可以表示成为“正则化项+损失函数”[8]形式的优化问题。以二分类为例,对于独立同分布的训练样本集 S={(X1,y1),...,(Xm,ym)}∈Rn×{+1,-1},求解下述优化问题:

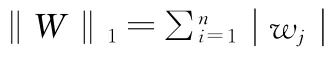
最初的机器学习算法主要考虑如何进行核最优化以提高决策函数的泛化能力,传统的算法难以高效地对大规模数据进行处理。实际上,机器学习理论关注可以实现的,行之有效的学习算法。很多推论问题属于无程序可循难度,所以部分的机器学习研究是开发容易处理的近似算法。大量实验表明线性分类决策函数能够有效地分类高维数据。没有先验知识告诉我们最优化问题的精确解对应的分类面就一定是泛化能力最强的,而诸多实验却表明近似最优解通常比精确解提供更好的分类面,因此专门针对线性核的训练算法受到广泛关注。从近五年机器学习顶级会议ICML和NIPS发表论文的质量和数量,足以看出研究者对这一热点问题的关注程度,也涌现出一些高效实用的海量数据分析方法。比较著名的方法主要有[9~11]:随机(次)梯度下降算法(Stochastic Gradient Descent,SGD);割平面方法(SVMperf)[12],bundle 方 法[13]和 置 信 域 牛 顿 方 法(TRON)[14]以及坐标优化算法[15~16]。这些算法能够较为有效解地决大规模线性问题,获得快速而稳定的收敛结果。
本文介绍近年来机器学习的一些代表性算法、发展趋势以及分析常用方法和技巧,进而对大规模机器学习问题的应用机理进行分析探讨。
3 求解大规模机器学习问题研究现状
大规模数据的学习问题给机器学习带来了新的挑战。因此,对于这类问题的求解就不再是一般意义上的优化问题,随之转化为机器学习问题。经典优化方法花费大量时间寻找给定精度下的最优解。与经典方法不同的是,大规模数据的优化不再要求是精确解,而是要突破计算机存储空间的瓶颈和计算开销的负担,让算法既快又准确地运行,寻找最具有测未知样本的决策函数并得到理想的分类器。传统的批处理算法由于无法突破计算机存储空间的瓶颈和计算开销的负担而失效。下面主要围绕线性核的形式,在“正则化项+损失函数”框架下介绍当前求解此类大规模机器学习问题的研究和发展的现状。
3.1 在线算法理论和实现

直到2007年,Shalev-Shwartz等人[10]提出的投影次梯度算法Pegasos,第一次在大规模数据上取得了实质性的成功,处理来自路透社的文本分类rcv1问题(800,000训练样本)只需不到5秒钟时间,这对于以前的算法是无法想象的。与其它算法相比,在线算法的优势明显。至此,在线算法的研究无论是在理论还是应用上都取得了比较成功的第一步,也引起了众多学者的强烈关注。
3.2 投影算子和截断算子方法
Pegasos在L2正则化问题(SVM)上取得相当的成功后,人们自然想拓广这种方法求解一般形式的正则化损失函数优化问题,即“L1正则化项+损失函数”的形式。针对L1正则化大规模在线算法的求解,2008年Duchi提出了高效的L1投影算子[19],可以将L1正则化问题转化为L1投影的梯度方法来解,但同时付出了klogn的计算代价(k是解向量非零特征个数),实现起来也很复杂。2009年,著名学者Langford[20]指出,随机梯度(SGD)方法在实际使用过程中并不具有稀疏性。为避免L1投影算子的计算复杂性问题,同时为确保在线算法解的稀疏性,他提出了截断梯度(Truncated Gradient)的方法[20]。该方法是一种为达到稀疏性目的而强制在梯度上进行的一种截断,并不具有明确的机器学习含义。尽管在形式上与Duchi的L1投影算子很相像,并且文献[20]在一定条件下也证明了这种方法的regret bound,但此时我们并不知道算法优化的目标函数是什么,这可能会涉及到复杂的非凸优化问题,同时也使得收敛速度难以分析,这使得L1的正则化的在线算法陷入了严重的困境。
3.3 结构优化策略
研究人员越来越意识到,正则化项和损失函数往往有着机器学习的特殊含义。同时,一些在线算法往往不能保证机器学习问题的结构,如在求解L1正则化学习问题时得不到稀疏性,收敛速度也缓慢。如何高效求解大规模机器学习问题并保证问题的结构是研究中的难点。早在1983年,Y.Nesterov[21]就指出如果能充分优化问题本身特殊的结构,可达到O(1/t)的收敛速率。随后Nesterov得到了多种形式的O(1/t)收敛速率的结构优化算法,比直接使用梯度的“黑箱(Black-Box)”方法要快一个数量级。结构优化的研究成果在优化领域产生了重要的影响,该方法又称为Proximal Gradient Method(PG)。所谓“黑箱”方法将正则化项和损失函数组成的目标函数作为一个整体来考虑,而不考虑各部分的细节,是凸优化方法在机器学习领域的直接应用。Y.Nesterov甚至曾经说过,“黑箱方法在凸优化问题上的重要性将不可逆转地消失,彻底地取而代之的是巧妙运用问题结构的新算法。”当然,并非所有问题的结构都能为我们所熟知,但至少机器学习问题的结构越来越明了地呈现在了研究者面前。
目前,结构优化算法已经被成功地应用解决一些机器学习问题,产生了极大的成功和极其重要的影响。2009年,Xiao的L1正则化在线学习算法(RDA)[22],不仅能够保证与批处理同等的稀疏性,算法的收敛速度也得到了保证,这是将结构优化思想与机器学习问题相结合的第一篇文章。机器学习结构优化方法的研究已经初现端倪,它为机器学习的研究注入了新的活力,一种新的机器学习优化问题求解模式由此展开篇章。而文献[23]的FOBOS则是RDA方法的一个特例。2009年Amir Beck等人[24]在Y.Nesterov的基础上对PG算法的理论进行了统一和完善,并在将其运用到图像复原正则化技术中,取得了很好的效果,不论是速度上还是图像复原度上均优于以往的算法。2010年Duchi[25]在Xiao RDA结构学习的框架内引入镜面下降(Mirror Descent,MD)方法求解大规模在线学习问题,并将其称之为复合目标镜面下降(Composite Objective Mirror Descent,Comid)。与RDA方法类似,Comid不仅保证了问题的结构,而且适用于光滑和非光滑的损失函数;但不同的是,Comid以瞬时梯度替代了RDA的平均梯度,使得Comid比RDA方法更加简洁和易操作[25]。Comid的在线算法做了充分的理论证明,得出不同损失和正则化项情况下的收敛速度。文献[22]和[25]成功的关键在于在优化过程中将正则化项和损失函数分别看待,对损失函数进行近似展开,对涉及正则化项的优化问题进行解析求解,从而减少了计算代价并保证了正则化项的结构。在理论上,文献[22]和[25]通过regret bound建立了在线优化和批处理优化之间的密切联系。
3.4 坐标优化算法
在大规模数据处理方面,除了在线优化方法,另一个值得关注的方法就是坐标优化算法。坐标优化方法的思路非常简单直观,主要是对高维优化问题采取各个击破的方法分而治之。具体的计算步骤就是固定其它维坐标,一次仅对选中的一维坐标进行优化求解。在线算法和坐标优化的主要区别是前者每一步迭代需要解单个样本关于所有维数的优化问题而后者每一步迭代需要解单维关于所有样本的优化问题。
Paul Tseng是坐标优化算法研究方面的著名学者,他从优化理论的角度对多种不同光滑性和凸性条件下的优化问题建立了坐标优化算法[26],其中也包括了机器学习正则化损失函数的优化问题。但Tseng的研究工作偏重于理论分析,缺乏解决实际问题和说明算法性能的实验。机器学习的一些研究者分别针对具体的学习问题提出了一些实用的坐标优化算法,并在真实数据库进行了大量的实验。
坐标优化方法来源于梯度下降原理,其主要思路是对一维优化子问题,根据偏导数得出下降方向,并根据目标函数的光滑性或者线搜策略进一步求出下降步长,通过在每个坐标方向上使目标函数不断递减,得到收敛性。在损失函数导数为Lipschitz连续的情形下可以根据Lipschitz常数求出步长,进而可以使用软阈值方法[24]得出单维子问题的下降步长,由于高维数据固有的稀疏性,这类方法适合求解L1正则化光滑损失函数的优化问题。
为了验证坐标优化算法在处理大规模实际问题的性能,一些研究者进行了广泛的实验比较,实验结果表明坐标优化是处理大规模稀疏数据特别是文本数据的首选算法[27]。鉴于坐标优化在解决大规模问题中如此重要的地位,林智仁教授继开发了著名的支持向量机软件包LibSVM[28]之后,又针对大规模稀疏数据的线性分类问题专门开发了Liblinear[29]软件包,Liblinear中的主要算法就是坐标优化算法。2010年,Nesterov对坐标优化方法进行了重新审视,指出坐标优化方法成功的关键在于利用了数据的稀疏性和使用了计算代价低的偏导数求取方法,在更新部分坐标的基础上使用最小化或梯度下降更新下一个坐标融入了更多的信息。因此,与全导数方法相比,坐标优化方法在不增加计算代价的基础上,往往会使目标函数下降得更快[32]。在这些分析的基础上,Nesterov提出了随机坐标优化方法,证明了随机坐标优化比使用全导数方法概率意义下收敛的速度会更快,具有处理海量数据(hugescale)的能力。
4 结语
回顾大规模机器学习优化问题的发展历程,在线和坐标优化两种方法在求解高维大样本问题时,各有优势和特点。在线方法主要利用大规模数据独立同分布的统计规律,而坐标优化主要利用高维数据稀疏的特性,可以认为这两种算法是机器学习的主流优化方法。单变量子问题解析解和结构优化策略是对在线和坐标优化算法的丰富和拓展。在线和坐标优化方法能够充分地利用了机器学习问题自身的特点,很好地满足了机器学习问题大规模和结构的实际需求。因此,求解具有结构特点的大规模机器学习优化问题是当前机器学习发展中的关键性科学性问题之一,是时代发展的迫切需求,对机器学习的发展也会产生深远的影响。
[1]边肇祺,张学工,等.模式识别 [M].北京:清华大学出版社,2000:18-26.
[2]周志华.机器学习[J].中国计算机学会通讯,2009,5(8):6-6.
[3]R.O.Duda,P.E.Hart,D.G.Stork.Pattern Classification[M].Second ed.New York:Wiley,2001.
[4]V.Vapnik.统计学习理论的本质 [M].张学工,译.北京:清华大学出版社,2000:32-36.
[5]B.E.Boser,I.Guyon,and V.N.Vapnik.A training algorithm for optimal margin classifers C//In proceedings of the Fifth Annal Workshop of Computational Learning Theory,PittsburgACM,1992,5:144-152.
[6]Friedman,J.,Hastie,T.and Tibshirani,R.Additive logistic regression:A statistical view of boosting(with discussion)[J].The Annals of Statistics,2000,28:337-407.
[7]T.Zhang.Statistical behavior and consistency of classification methods based on convex risk minimization[J].The Annals of Statistics,2004,32:56-85.
[8]Tong Zhang.Adaptive forward-backward greedy algorithm for sparse learning with linear models[C]//In Advances in Neural Information Processing Systems,2008.
[9]Zhang,T.Solving large scale linear prediction problems using stochastic gradient descent algorithms[C]//Proc of the 21th International Conference on Machine Learning,2004:919-926.
[10]Shalev-Shwartz,S.,Singer,Y.,& Srebro,N.Pegasos:primal estimated sub-gradient solver for SVM[C]//Proc of the 24th International Conference on Machine Learning,2007:807-814.
[11]Bordes,A.and Bottou,L.Careful quasi-Newton stochastic gradient descent[J].Journal of Machine Learning Research.2009(10):1737-1754.
[12]Joachims,T..Training linear SVMs in linear time[C]//Proc of the of the 12th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining,2006,33:82-95.
[13]Smola,A.J.,Vishwanathan,S.V.N.,& Le,Q..Bundle methods for machine learning[C]//Advances in Neural Information Processing Systems 20,Cambridge MA,2007,20:1377-1384.
[14]Lin,C.-J.,Weng,R.C.,& Keerthi,S.S.Trust region Newton method for large-scale logistic regression[J].Journal of Machine Learning Research,2008(9):627-650.
[15]Chang,K.-W.,Hsieh,C.-J.,& Lin,C.-J..Coordinate descent method for large-scale L2-loss linear SVM[J].Journal of Machine Learning Research,2008(9):1369-1398.
[16]Hsieh,C.J.,Chang,K.W.,Lin,C.J.,Keerthi,S.S.,and Sundararajan,S.A dual coordinate descent method for largescale linear SVM[C]//Proc of the 25th International Conference on Machine Learning,2008:408-415.
[17]M.Zinkevich.Online convex programming and generalized infinitesimal gradient ascent[C]//Proc of the 20th Interna-tional Conference on Machine Learning,2003.
[18]Hazan,E.,Kalai,A.,Kale,S.,&Agarwal,A..Logarithmic regret algorithms for online convex optimization[J].COLT,2006.
[19]Duchi,J.,Shalev-Shwartz,S.,& Singer,Y.Efficient projections onto the l1-ball for learning in high dimensions[C]//Proc of the 25th International Conference on Machine Learning,2008:272-279.
[20]J.Langford,L Li and T.Zhang.Sparse online learning via truncated gradient[J].Journal of Machine Learning Research,2009,10:777-801.
[21]Nesterov,Y.A method of solving a convex programming problem with convergence rate O(1/k2)[J].In Soviet Mathematics Doklady,1983,27:372-376.
[22]Xiao,L.Dual averaging methods for regularized stochastic learning and online optimization[J].Journal of Machine Learning Research,2010,11:2543-2596.
[23]J.Duchi and Y.Singer.Efficient online and batch learning using forward backward splitting[J].Journal of Machine Learning Research,2009,10:2899-2934.
[24]Beck and M.Teboulle.Mirror descent and nonlinear projected subgradient methods for convex optimization[J].Operations Research Letters,2003,31:167-175.
[25]John Duchi,Shai Shalev-Shwartz,Yoram Singer,and Ambuj Tewari.Composite objective mirror descent[J].In COLT,2010b.
[26]Z.-Q.Luo and P.Tseng[J].On the convergence of coordinate descent method for convex differentiable minimization[J].Journal of Optimization Theory and Applications,1992,72(1):7-35.
[27]Chang C C,Lin C J.A Library for Support Vector Machines[DB/OL].http://www.csie.ntu.edu.tw/~cjlin/libsvm/
[28]C.-H.Ho and C.-J.Lin.LIBLINEAR—A Library for Large LinearClassification[DB/OL].http://www.csie.ntu.edu.tw/~cjlin/liblinear/
[29]Yuan,G.X.,Chang,K.W.,Hsieh,C.J.,and Lin,C.A comparison of optimization methods for large-scale L1-regularized linear classification [J].Methods,2010,1:1-51.
[30]杨凌霄,武建平.机器学习方法在人脸检测中的应用[J].计算机与数字工程,2008,36(3).
[31]鲁庆明,徐东平.基于支持向量机和纹理特征的人脸识别[J].计算机与数字工程,2010,38(10).
[32]Nesterov,Y.Efficiency of coordinate descent methods on huge-scale optimization problems.[R].Belgium:University catholique de Louvain,Center for Operations Research and E-conometrics(CORE),2010:02-20.http://130.104.5.100/cps/ucl/doc/core/documents/coredp2010_2web.pdf.

