基于规范化的B样条密度模型的聚类算法

刘 哲, 谭振江, 王洪君

(1. 吉林师范大学 计算机学院, 吉林 四平 136000； 2. 江苏大学 电气信息工程学院, 江苏 镇江 212013)

0 引 言

聚类分析在模式识别和图像处理领域中具有广泛的应用前景[1,2]。图像识别和图像分割是其主要的应用方面, 目前研究已经取得了许多成果。早在1979年, Coleman和Andrews就提出了用聚类分析进行图像分割。Yao等[3]提出了基于数学形态学的K-means聚类算法实现图像分割。Zhao等[4]提出了广义的模糊C-means聚类算法实现灰度图像有效分割。Liu等[5]提出了一种结合空间信息的模糊谱聚类算法实现对噪声图像分割。这些方法大多数都是直接在图像上进行聚类分析, 由于图像的复杂性和无规律性, 存在很多缺陷。基于密度聚类方法是根据密度概念对数据对象进行聚类和分割的。它根据数据对象的密度或某种密度函数生成聚类。ISC(Intelligent Subspace Clustering)[6], Rough-DBSCAN(Density Based Spatial Clustering Applications with Noise)[7], DBSC(Density-Based Spatial Clustering)[8]等都是具有代表性的基于密度的聚类方法, 并在应用中表现了良好性能。

在基于密度的聚类方法中, 通常选择熟知的高斯、t、Poisson和α等分布。这些带有先验性质的参数化方法并非总能给出对各种医学图像合适的描述, 模型的基本假设与实际的物理模型之间存在较大差异, 即有“模型失配”问题。非参数密度估计方法在无需对模型做任何假设前提下, 具有有效拟合任意形式的概率分布性能, 文献[9]提出基于核密度估计(KDE: Kernel Denstity Estimate)的聚类方法, 该方法可有效地实现腹部CT图像分割, 但随着样本量增加计算量也不断增大, 而且存在平滑参数难以自适应估计及计算速度较慢等缺点。为此, 文献[10]提出了无监督的非参数正交多项式密度模型实现图像分割, 但随着样本量增加正交多项式密度估计以恒速率收敛, 而且正交多项式密度估计是一个函数而不是概率密度函数。

笔者以图像数据为研究对象, 利用B样条函数在函数逼近方面的优势, 在研究图像灰度密度分布基础上, 提出一种基于B样条密度函数的图像聚类算法。首先定义灰度图像的非参数标准化的B样条密度估计模型, 通过NNBEM(Non-parametric B-spline Expectation Maximum)算法估计模型的参数, 最后根据贝叶斯准则实现对图像的聚类。

1 传统的混合模型

设X={X1,X2,…,XN}为随机观察数据集,Xi是d维随机变量,Xi间相互独立,fi(x|θi)(i=1,2,…,K)是对应的概率密度函数, 其中,x∈Rd是Xi取值,θi是模型参数。若将Xi样本按一定权重混合后, 再从中任取一个进行观察, 则其概率密度函数

(1)

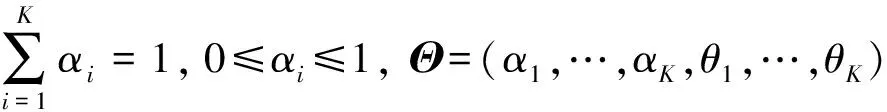
在有限概率混合模型中, 最常见的是高斯混合模型(GMM: Gaussian Mixture Model), 模型中每个高斯密度函数的未知参数θ=(α1,μ1,Σ1,α2,μ2,Σ2,…,αk,μk,Σk),μk为均值,Σk为协方差, 则用EM算法[11]进行极大似然估计。

算法1

1) 模型参数初始赋值。假设混合模型的分类数k已知, 对混合模型中各密度分布待估计参数θ进行初始设置。

2) 期望步。计算在第n次迭代时每个样本i属于第j类的后验概率

(2)

3) 最大化步。通过求解对数似然方程, 计算期望值到达极大值点时的参数： 均值μ, 协方差矩阵Σj及权重αj, 用于下次迭代

(3)

(4)

(5)

4) 满足结束条件则停止, 否则转至2)。

2 基于规范化的B样条密度模型的图像聚类

2.1 基于B样条密度函数的模型构造

在数值分析中, B样条[12]是样条曲线一种特殊的表示形式, 采用逼近原理构造曲线、 曲面, 保留了Bezier方法中的优点, 是B样条基曲线的线性组合, 也是目前广泛应用的一种拟合方法。

Curry和SchCoenberg提出d次(d=1,2,…)k(k=1,2,…)个节点的每个B样条曲线段表示为

(6)

(7)

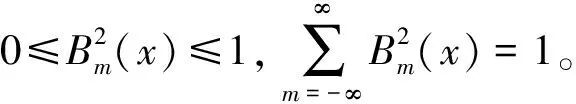
设x1,x2,…,xn是n个独立同分布f的随机样本, 线性组合f是多个B样条的混合, 则B样条密度函数估计为

(8)

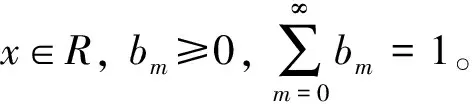
(9)

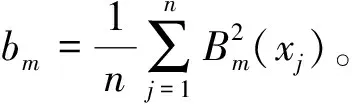
2.2 聚类算法

根据定义的非参数规范化的B样条密度模型, 不需要预先假设图像像素的条件概率密度函数, 直接根据样本数据估计出该数据场的概率密度函数。若模型中参数θk=(b0,k,…,bN-1,k)[11], 图像样本数据分类数k=1,…,K, 则fN(x)=f(x|θk)。采用NNBEM算法估计模型参数, 得到图像聚类结果。

算法2 (NNBEM算法)

输入： 图像样本数据X=(x1,…,xn)[12], 分类数K

输出： 聚类结果

Step1 Initialization: 使用K-means算法初始划分为K类, 并对参数进行初始化设置

(10)

(11)

其中nk是第k类包含的样本个数,l=0,…,N-1。

Step2 Expectation: 在m次迭代时, 像素xi属于第k类的后验概率

(12)

Step3 Maximization: 根据第m次迭代得到样本的后验概率, 第m+1次迭代更新参数为

(13)

(14)

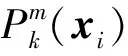
(15)

其中j(xi)表示像素xi的类别标签。

3 实验结果与分析

为验证提出的NNBEM算法效果, 该实验使用Dell公司图像专用工作站, Matlab7.0作为实验开发工具, 采用的模拟图像和实验数据来源于美国加州大学伯克利分校的BSDB标准测试图像数据库[13]。为验证聚类算法的聚类性能, 对该算法与非参数正交多项式混合模型的聚类算法(SNEM: Stochastic Nonparametric Expectation Maximum)[10]进行了比较。为评价聚类算法性能, 采用指标VI(Variation of Information)、 ARI(Adjusted Rand Index)[14]和F-measure[15]衡量。

对于有n个样本的数据集, VI利用参考聚类图像的熵和实际聚类结果的熵计算获得, 用来衡量实际聚类结果相对参考聚类结果的信息变化, VI值越小, 其聚类结果越准确。计算如下

VVI(S,S′)=H(S)+H(S′)-2I(S,S′)

(16)

其中H和I分别表示聚类结果的熵和S和S′两个聚类结果之间的互信息。其计算如下

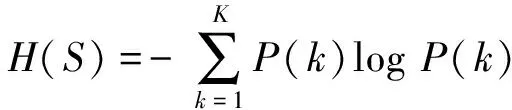
(17)

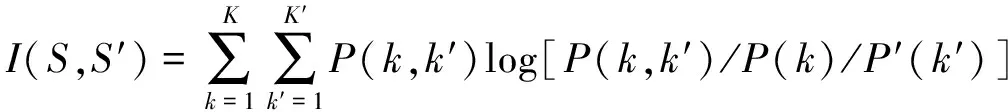
(18)

其中P(k)为图像中任意一个像素属于第k个聚类的概率；P(k,k′)为像素在S中属于第k个聚类并且同时在S′中属于第k′个聚类的联合概率。

指标ARI把样本类别划分看作是它们之间一种关系, 或将样本分在同一类, 或在不同类, 通过统计正确聚类对数评价算法性能。对于有n个样本的数据集, ARI计算如下

(19)

其中nkk′为被划分到类别k类别k′的样本个数；AARI(S,S′)值越大, 聚类的正确率越高。

a 原始图像 b 聚类结果

3.1 模拟图像

采用模拟图像, 其灰度取值范围Ω={0,1,…,255}, 有3个聚类Λ={1,2,3}, 图像大小为237×237像素。模拟图像分割结果如图1所示。从图1中可看出, 通过笔者算法可实现对模拟图像的准确聚类。

3.2 真实图像聚类

实验数据来源于美国加州大学伯克利分校的BSDB标准测试图像数据库[12], 对非参数正交多项式密度模型的SNEM聚类算法与笔者的NNBEM聚类算法进行比较的结果如图2所示。

图2a为原始图像, 图2b非参数正交多项式混合模型SNEM算法聚类结果[10], 图2c为笔者NNBEM算法聚类结果。从视觉角度看, 笔者提出的方法效果优于SNEM聚类算法。

a 原图 b SNEM算法 c 笔者NNBEM算法 d 人工分割

为量化聚类划分的性能, 对上述图像数据每种算法分别运行20次, 计算其评价指标VI、 ARI及F-measure的平均值如表1所示。从实验结果可看出, 笔者聚类算法NNBEM的VI指标值小于SNEM算法, 其聚类结果较SNEM算法更准确； 笔者聚类算法ARI及F-measure值均大于SNEM算法, 其聚类性能都优于基于非参数正交多项式的SNEM聚类算法。

表1 两种算法聚类算法性能比较

4 结 语

笔者提出了一种规范化的B样条密度模型的图像聚类算法。通过定义非参数规范化B样条混合模型, 利用EM算法估计B样条混合模型参数, 最后根据贝叶斯准则实现图像聚类。该算法有效地克服了有参混合模型对每个模型分布的假设带来的不一致问题及目前存在的非参数正交多项式密度函数不是概率密度函数的缺陷。实验结果表明, 该算法优于SNEM算法, 对图像聚类效果较好, 准确率高。算法的计算复杂度高于SNEM算法及对初始值仍比较敏感, 如何在聚类性能和计算复杂度之间进行折中以及如何设定初始值不影响聚类性能问题, 将是下一步研究的重点。

参考文献：

[1] KANNAN S R, DEVI R, RAMATHILAGAM S, et al. Effective FCM Noise Clustering Algorithms in Medical Images [J]. Computers in Biology and Medicine, 2013, 43(2): 73-83.

[2]曲福恒, 胡雅婷, 马驷良, 等. 一种高效鲁棒的无监督模糊c均值聚类算法 [J]. 吉林大学学报: 理学版, 2012, 50(6): 1179-1184.

QU Fu-heng, HU Ya-ting, MA Si-liang, et al. An Efficient and Robust Clustering Algorithm for Unsupervised Fuzzy c-Means [J]. Journal of Jilin University: Science Edition, 2012, 50(6): 1179-1184.

[3]YAO Hong, DUAN Qing-ling, LI Dao-liang, et al. An Improved-Means Clustering Algorithm for Fish Image Segmentation [J]. Mathematical and Computer Modelling, 2013, 58(3/4): 784-792.

[4]ZHAO Feng, JIAO Li-cheng, LIU Han-qiang. Kernel Generalized Fuzzy C-Means Clustering with Spatial Information for Image Segmentation [J]. Digital Signal Processing, 2013, 23(1): 184-199.

[5]LIU Han-qiang, ZHAO Feng, JIAO Li-cheng. Fuzzy Spectral Clustering with Robust Spatial Information for Image Segmentation [J]. Applied Soft Computing, 2012, 12(11): 3636-3647.

[6]JAHIRABADKAR S, KULKARNI P. Isc-Intelligent Subspace Clustering, A Density Based Clustering Approach for High Dimentsional Dataset [J]. World Academy of Science, Engineering and Technology, 2009, 55: 69-73.

[7]VISWANATH P, SURESH BABU V. Rough-DBSCAN: A Fast Hybrid Density Based Clustering Method for Large Data Sets [J]. Pattern Recognition Letters, 2009, 30(16): 1477-1488.

[8]LIU Qi-liang, DENG Min, SHI Yan, et al. A Density-Based Spatial Clustering Algorithm Considering Both Spatial Proximity and Attribute Similarity [J]. Computers & Geosciences, 2012, 46: 296-309.

[9]XIE Cong-hua, SONG Yu-qing, LIU Zhe. Density-Based Clustering Algorithm Using Kernel Density Estimation and Hill-down Strategy [J]. Journal of Information & Computational Science, 2010, 7(1): 135-142.

[10]刘哲, 宋余庆, 陈健美, 等. 基于二类切比雪夫正交多项式非参数混合模型的图像分割 [J]. 计算机研究与发展, 2011, 11(48): 2008-2014.

LIU Zhe, SONG Yu-qing, CHEN Jian-mei, et al. Image Segmentation Based on Non-Parametric Mixture Models of Chebyshev Orthogonal Polynomials of the Second Kind [J]. Journal of Computer Research and Development, 2011, 11(48): 2008-2014.

[11]MELNYKOV V, MELNYKOV I. Initializing the EM Algorithm in Gaussian Mixture Models with an Unknown Number of Components [J]. Computational Statistics & Data Analysis, 2012, 56(6): 1381-1395.

[12]颜庆津. 数值分析 [M]. 北京： 北京航空航天大学出版社, 1992.

YAN Qing-jin. Numerical Analysis [M]. Beijing: Beihang University Press, 1992.

[13]FOWLKES C, MARTIN D, MALIK J. The Berkeley Segmentation Dataset and Benchmark(BSDB). [2013-02-10]. [DB/OL]. http://www.cs.berkeley.edu/projects/vision/grouping/segbench.

[14]WANG Li-jun, DONG Ming. Multi-Level Low-Rank Approximation-Based Spectral Clustering for Image Segmentation [J]. Pattern Recognition Letters, 2012, 33(16): 2206-2215.

[15]STEINBACH M, KARYPIS G, KUMAR V. A Comparison of Document Clustering Techniques [C]∥Proc of the KDD Workshop on Text Mining. Boston, USA: [s.n.], 2000: 109-111.