基于模型预测的无人机组合陀螺在线标定

贾鹤鸣, 宋文龙, 牟宏伟, 车延庭

(1. 东北林业大学 机电工程学院, 哈尔滨 150040； 2. 中国运载火箭技术研究院, 北京 100076；3. 哈尔滨工程大学 自动化学院, 哈尔滨 150001)

0 引 言

对于捷联惯性导航系统(SINS: Strap Down Inertial Navigation System), 由于工作时间长、 环境等因素的变化, 陀螺漂移会导致标定值产生很大差异, 使系统无法满足对准、 导航精度的要求[1,2]。为改善这种状况, 笔者提出了捷联惯性导航系统/天文导航系统(SINS/CNS： SINS/Celestial Navigation System)组合陀螺在线标定方法。

捷联惯导系统通常利用卡尔曼滤波(KF: Kalman Filter)方法实现标定, 但其精度在很大程度上由系统的能观测性所决定； 同时, 它需要建立比较准确的系统状态空间模型[3]。而模型预测滤波(MPF:Model Prediction Filter)是一种基于非线性系统模型的实时滤波方法, 克服了卡尔曼滤波的缺点, 能在线估计任何形式的未知模型误差, 降低了系统的维数, 计算速度快, 具有良好的鲁棒稳定性[4]。

1 SINS/CNS组合在线标定陀螺输出误差模型

陀螺仪长时间工作, 由于环境变化等因素会引起陀螺漂移、 标度因数误差和陀螺安装轴不正交误差等因素的变化, 为更好地估计陀螺漂移后修正惯性器件误差, 将陀螺误差源建入陀螺模型得陀螺测量值

ωg=ω+b+K+τ+ng

(1)

(2)

其中S为刻度因数误差阵,ω为陀螺实际输出的角速度；Δxy,Δxz,Δyx,Δyz,Δzx,Δzy为陀螺的安装误差角。

2 模型预测滤波基本算法

模型预测滤波(MPF： Model Prediction Filter)是利用预测输出跟踪测量输出, 估计系统的模型误差, 将模型误差作为估计量, 利用观测量纠正模型中不确定的误差[5,6]。

假设一个非线性系统如下

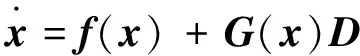
(3)

Z=h(x)+v

(4)

其中f∈Rn是连续可微的非线性函数,x∈Rn是状态变量,D∈Rq是模型误差向量,G∈Rn×q是模型误差分布矩阵。Z∈Rm是量测向量,v是量测噪声向量, 并假定其为零均值的高斯白噪声, 协方差为E{vvT}∈R。

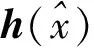
(5)

根据李导数定义k阶李导数

缺血性脑血管病好发于中老年人，近年来发病率越来越高[1] 。绝大多数患者患病与颈动脉粥样硬化有着密切关系。而症状性颈动脉狭窄是导致动脉粥样硬化的主要病变，针对此病应于恰当的时间给予外科手术干预[2] 。本研究收集2015年7月至2017年11月大连市中心医院诊治的30例症状性颈动脉狭窄患者的临床资料，通过比较颈动脉内膜切除术(carotid endarterctomy,CEA)术前与术后狭窄率及颈内动脉收缩期峰值流速，分析其治疗效果。

(6)

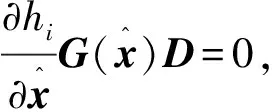
(7)

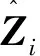
(8)

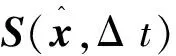
(9)

Λ(Δt)∈Rm×m为对角阵, 其对角元素为

(10)

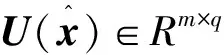
(11)

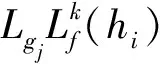
(12)

定义性能指标函数

(13)

其中W∈Ru×u是模型误差加权矩阵。

假定小的时间间隔为常数, 则Z(t)=Zk,Z(t+Δt)=Zk+1。为使J最小, 需要满足条件∂J/∂Dk=0, 由此可得到[tk,tk+1]时间区间内的模型误差估计

(14)

3 基于模型预测的SINS/CNS组合陀螺在线标定混合滤波方法

3.1 SINS/CNS组合陀螺在线标定方法

首先取误差四元数的矢量部分和陀螺漂移误差6维完全可观测变量为状态变量, 以误差四元数的矢量部分作为观测量, 利用卡尔曼滤波算法估计陀螺漂移； 将估计的陀螺漂移平均值建入陀螺误差模型, 再取误差四元数的矢量部分和陀螺漂移平均值共6维变量为状态变量, 刻度因数估计误差和安装误差估计误差共9维变量为模型误差向量, 误差四元数的矢量部分为观测量, 利用模型预测滤波估计陀螺刻度因数误差和安装误差。

3.2 基于模型预测混合滤波方法的状态方程和量测方程

⊗q=[δq,δe1]T

(15)

由四元数运动学方程有

(16)

对式(15)求导, 并将式(16)代入得

(17)

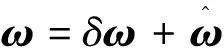
(18)

(19)

将式(18)代入(17)得

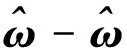
(20)

将式(19)和式(21)代入式(20)后对其线性化, 得

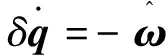
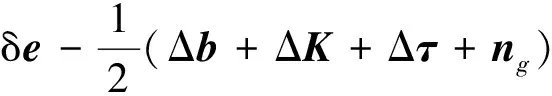
(22)

将式(2)代入式(22), 写成矩阵形式为

(23)

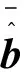
(24)

根据模型预测滤波算法, 系统状态方程为

(25)

其中F∈R6×6是系统状态转移矩阵,X∈R6是状态变量,G1∈R6×6是模型误差分布阵,D∈R9是模型误差向量,G2∈R6×6是系统噪声驱动阵,W∈R6是系统噪声。

取δq1的矢量部分δe作为观测量

(26)

系统量测方程为

Z(t)=HX(t)+V(t)

(27)

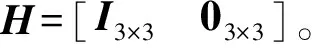
根据第2节中模型预测滤波基本算法, 取pi=1,n=6,u=3,m=9, 可得

根据模型预测滤波步骤, 应用模型预测滤波算法, 对刻度因数和安装误差进行估计。

4 仿真研究

4.1 仿真条件

假设无人机的初始位置为东经126.63°, 北纬47.75°, 高度是5 000 m； 载体匀速飞行且飞行速度为150 m/s, 飞机做航向变化的姿态机动, 1 200 s方位角改变60°； 0～10 min采用KF估计陀螺漂移, 10～20 min切换滤波方式, 采用MPF估计刻度因数和安装误差； 初始航向角为30°, 初始俯仰角为0, 初始横滚角为0； 方位失准角5角分, 水平失准角20角秒； 陀螺常值漂移为0.01°/h； 刻度因数误差为50×10-3‰； 安装误差为3角分； 仿真时间为1 200 s, 采样周期为1 s。

4.2 仿真结果分析

安装偏差角的估计结果只给出Δzx,Δzy,Δyz的情况。从图1～图3可看出, 经过SINS/CNS组合在线标定, 陀螺仪的零偏标定误差在万分之几度/小时级别上, 陀螺仪的刻度因数误差小于3×10-3‰, 陀螺仪的安装误差角误差也小于0.06角分, 估计结果均收敛于设置值, 标定结果比较理想。由图2和图3可看出, 10 min后切换滤波方式, 利用模型预测滤波有效地估计了陀螺刻度因数和安装误差, 收敛速度快, 同时保证了滤波的数值稳定性。

图1 模型预测混合滤波陀螺漂移仿真曲线

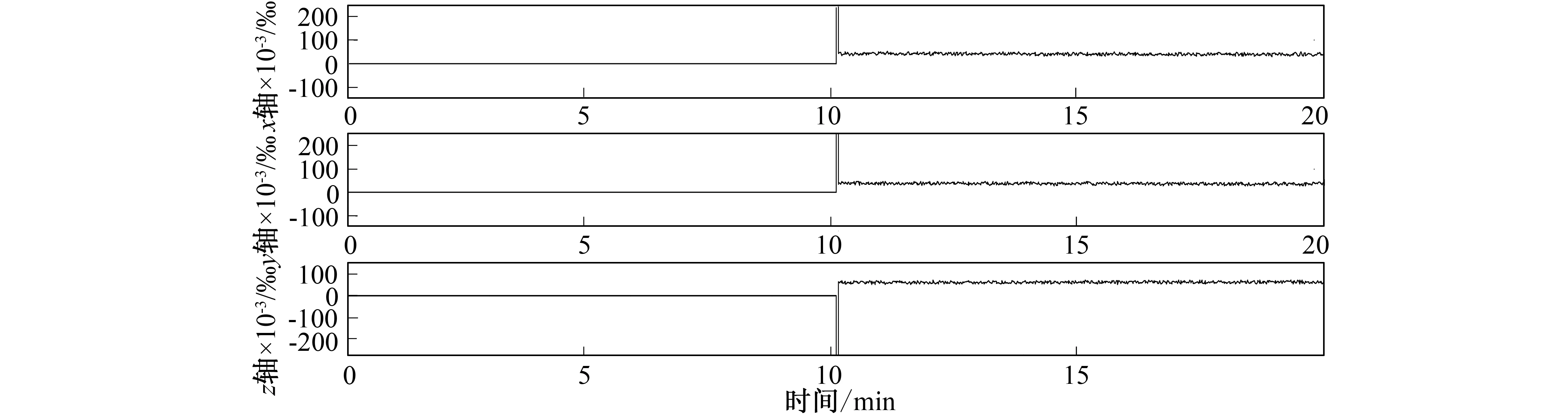
图2 模型预测混合滤波陀螺刻度因数仿真曲线

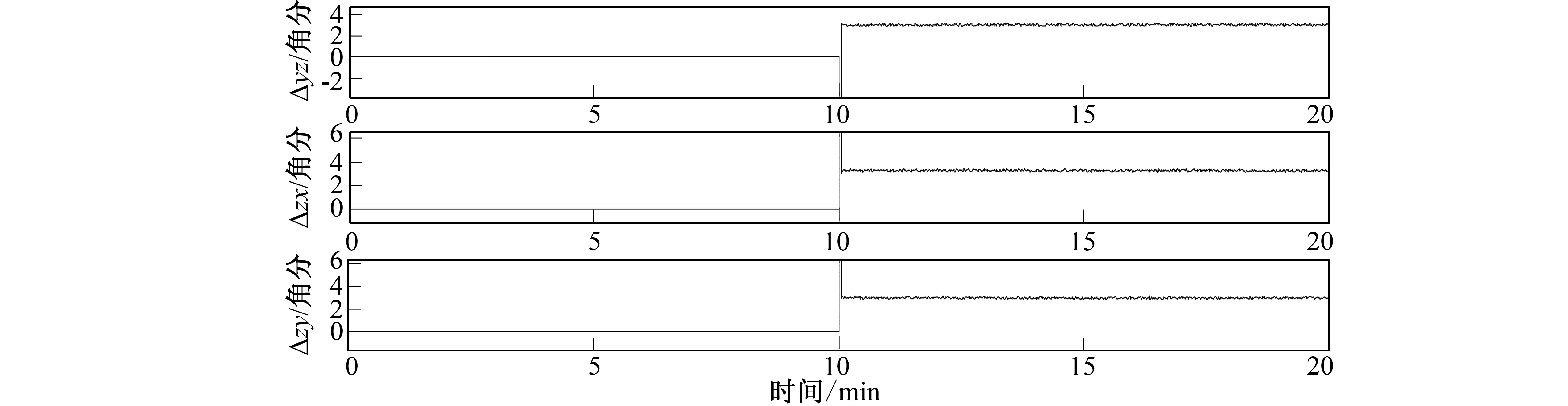
图3 模型预测混合滤波陀螺安装误差仿真曲线

5 结 语

笔者对KF-MPF混合滤波在SINS/CNS组合陀螺在线标定的应用进行了研究, 分析了MPF的数学机理。实验仿真结果表明, KF-MPF混合滤波能很好地适用于在线标定中, 避免了线性化的局限, 而且不需要建立准确的状态空间模型, 提高了可靠性。同时, KF-MPF混合滤波可减少计算量, 保证了数值稳定性。结果证明了KF-MPF混合滤波在陀螺在线标定中的可行性和优越性, 具有工程应用价值。

参考文献：

[1]张树侠, 孙静. 捷联式惯性导航系统 [M]. 北京： 国防工业出版社, 1992： 6-10.

ZHANG Shu-xia, SUN Jing. Strap Down Inertial Navigation System [M]. Beijing: National Defence Industrial Press, 1992： 6-10.

[2]白俊卿, 卫育新. 车载SINS/GPS组合导航系统的在线标定算法 [J]. 电子设计工程, 2010, 18(2)： 89-90.

BAI Jun-qing, WEI Yu-xin. Arithmetic of Vehicular SINS/GPS Integrated Navigation System’s On-Line Calibration [J]. Electronic Design Engineering, 2010, 18(2)： 89-90.

[3]CHOUKROUN D, WEISS H, ITZHACK Y, et al. Kalman Filtering for Matrix Estimation [J]. IEEE Transactions on Aerospace and Electronic System, 2006, 42(1)： 147-159.

[4]郑庆辉. 基于GPS的航天器姿态、 相对姿态确定研究 [D]. 长沙： 国防科技大学航天科学与工程学院, 2003.

ZHENG Qing-hui. GPS Based Absolute and Relative Attitude Determination of Spacecraft [D]. Changsha: College of Space Science and Engineering, National University of Defense Technology, 2003.

[5]LU Ping. Nonlinear Predictive Controllers for Continuous Systems [J]. Journal of Guidance Control and Dynamics, 1994, 17(3)： 553-560.

[6]LU Ping. Optimal Predictive Control of Continuous Nonlinear Systems [J]. International Journal of Control, 1995, 62(3)： 633-649.

[7]陈少华. 高轨机动航天器SINS/GNSS/CNS自主导航技术研究 [D]. 南京： 南京航空航天大学自动化学院, 2012.

CHEN Shao-hua. Research on Autonomous SINS/GNSS/CNS Navigation for High Orbit Vehicle Transfering [D]. Nanjing: College of Automation, Nanjing University Aeronautics and Astronautics, 2012.

[8]陈哲. 捷联惯性导航系统原理 [M]. 北京：中国宇航出版社, 1986.

CHEN Zhe. Strap Down Inertial Navigation System Principle [M]. Beijing: China Astronautics Publishing House, 1986.

[9]贾鹤鸣, 宋文龙, 牟宏伟, 等. ISR-CDKF在SINS大方位失准角初始对准中的应用 [J]. 吉林大学学报: 信息科学版, 2013, 31(2)： 196-202.

JIA He-ming, SONG Wen-long, MU Hong-wei, et al. Application of ISR-CDKF in Initial Alignment of Large Azimuth Misalignment in the SINS [J]. Journal of Jilin University: Information Science Edition, 2013, 31(2)： 196-202.