基于改进DBSCAN算法的高性能计算中心用户分类的研究及应用

徐海啸, 麻 婧, 吴 旗

(吉林大学 a. 计算机科学与技术学院； b. 高性能计算中心, 长春 130012)

0 引 言

数据挖掘是指从数据库的大量数据中揭示出隐含的、 先前未知的并有潜在价值信息的非平凡过程。聚类分析则是数据挖掘中的一个研究方向。聚类的目标是将数据分类到不同的类或簇, 使同一簇中对象有很大的相似性, 而不同簇间的对象有很大的相异性。聚类分析可应用于各种用户数据的分类中, 如民航客户分类[1]以及电信客户分类[2]。

DBSCAN(Density Based Spatial Clustering of Applications with Noise)算法[3]是基于密度的聚类分析算法, 对噪声有抵抗性, 并且能发现任意形状的类簇,但却对初始参数E(邻域半径)和MPts(E邻域最小点数)非常敏感[4]。

针对这一缺点, 近些年出现了一些改进研究。文献[5]提出了K-dist图的思想, 主要解决了类之间包含和交叉关系。文献[6]采用对象投影的方法, 考察对象的临域平衡性, 使用平衡密度可达聚簇, 有效排除了边界稀疏对象的噪声。文献[7]采用选取核心对象邻域中的代表对象扩展类, 相比文献[5,6]算法, 提高了算法时间性能。其他聚类算法的改进思路也可应用到DBSCAN算法中, 如文献[8]提出的加速k-means算法, 利用迭代调整簇阈值的方法将簇中心迁移, 这一思路与文献[9]中通过构建网格密度矩阵划分密度阈值, 从而解决DBSCAN参数选取困难的方法相似。文献[9]中提到的MDBSCAN算法相比于上述算法能有效发现密度相差较大的簇, 但由于其使用了从密到疏的分阶段聚类方法, 对初始参数的依赖性依然很大。

为更大程度地降低初始参数的影响, 笔者提出了改进算法, 即在MDBSCAN[9]的基础上添加了簇排序队列。改进的算法相比于MDBSCAN更注重数据的内部簇结构。在聚类的同时引入可表达簇信息的队列, 根据队列的信息寻找下一个扩展点, 因此, 降低了选点的随机性。同时, 变化的队列相当于可变参数, 在每层次阈值的建簇中起到调整初始参数的作用, 因此, 降低了参数的依赖性。

将改进的DBSCAN算法应用到高性能计算中心用户分类中, 可发现用户群体行为的共性。通过进一步分析不同用户群体提交作业和申请资源的特点, 可帮助不同用户建立资源使用策略。这对提高集群整体资源的使用效率有很大意义。

1 DBSCAN算法的主要缺点

DBSCAN算法的思想是利用密度连通特性, 即要求聚类空间中一定区域内对象的数目不小于某一给定阈值, 从而快速发现任意形状的类。但是, 由于它使用了全局性表征密度的参数, 因此在聚类密度不均匀或聚类间距离差距较大时, 聚类质量也较差[10,11]。

确定初始参数E的方法是用户指定的, 因此很难具有确定性。当数据密度和类间距离分布不均匀时, 较大的E的初值选取导致将较稀的类的对象误认为是边界对象, 而较小的E的初值选取会将不同的类合并为同一类, 从而降低聚类的精度。然而, 真实世界的数据集合往往分布不均。因此, 全局的密度参数不能刻画数据集的内在聚类结构。

对DBSCAN算法的改进比较著名的是OPTICS(Ordering Points to Identify the Clustering Strueture)算法, 其思想是对数据库中所有对象进行排序, 找出簇结构的信息, 从而确定合适的E值。但由于其复杂的处理方法以及大量的I/O操作, 使其运行速度远低于DBSCAN。

2 DBSCAN改进算法

2.1 采用多密度阈值解决输入参数E的全局性

当密度不均匀分布时, 需要用不同的邻域半径值作为聚类标准。所以, 只要将数据空间按照密度大小进行划分, 同一密度空间的数据按相同参数E进行聚类即可[9]。

数据空间的密度划分方案可采用网格划分的方法。将数据空间表示为网格形式的密度分布图, 统计不同密度的网格数量。将分布图的峰值作为网格密度阈值, 按等效规则转化为DBSCAN算法中的各个E值。最后将整个数据空间按网格密度从密到疏分阶段进行局部聚类。

等效规则的核心思想是： 相同容积内的对象数目相同。在基于网格的CLIQUE(Clustering In Quest)算法中, 将n维空间划分为长方形单元, 通过比较单元中数据点个数与输入模型参数k, 判断单元的密集程度。DBSCAN算法在思想上与CLIQUE相同, 只是用半径为E的n维球形区域进行度量, 因此可将两者进行等效[12]。即

(1)

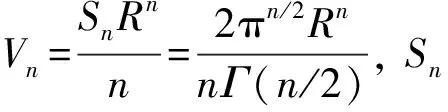
2.2 采用簇排序序列减小输入参数MPts对聚类结果的影响

DBSCAN算法在选取下一个核心点时具有随机性, 并没有考虑数据的内部簇结构。通过增加一个簇排序队列可解决该问题。

簇排序队列存储核心对象及其直接密度可达对象, 并按可达距离升序排列。每次选取该队列中距离最小的样本点进行拓展。簇排序队列的更新是通过求出每次选取核心点直接密度可达点的可达距离, 对队列进行重新排序。簇排序信息相当于一个可变的参数, 使输入参数的变化不会影响样本点的相对输出顺序。

算法中的直接密度可达的定义如下： 给定一个对象集合D, 如果p在q的E邻域内, 而q是一个核心对象, 则称对象p从对象q出发时是直接密度可达的。

3 算法描述

3.1 算法基本流程

1) 将表示x轴和y轴的n维数据分别向一维映射, 数据做归一化处理, 形成平面散点图。

2) 对数据空间进行网格划分, 一般以值域的1/20～1/50进行划分, 网格宽度记为B。

3) 统计网格内点数目, 统计各层次的数据密度占有的网格数, 从而计算密度阈值的划分层次。

4) 对每个层次的密度阈值根据等效规则计算参数E(MPts设定为4)。

5) 选取密度最高的网格单元,任选一个数据进行类扩展, 具体方法如下:

① 创建两个队列R1,R2。R1用于存储核心对象及其直接可达对象, 并按可达距离升序排列。R2用于存储已确定分类的样本点。

② 若该密度的样本集中所有点都处理完毕, 则进入步骤④; 否则, 选一个不在R2且为核心对象的样本点, 并找到其直接密度可达点, 存入R1中并排序。

③ 从R1中取出可达距离最小的样本点进行拓展, 并保存至R2中。若该点已经存在于R2中, 且具有更小的可达距离, 则用此点取代旧点, 并将R1重新排序。

④ 该密度阈值的簇聚类完毕, 进入步骤6)。

6) 采用低一级的密度阈值, 重复步骤5), 直至完成最低一级密度阈值的聚类。

3.2 算法伪代码

算法首先求出每个层次的密度阈值[9], 即先求得每个网格内的点数目, 并绘制密度分布图, 由分布图的每个峰值作为密度阈值, 算法的伪代码如下：

procedure threshold_value (U)

begin

if(pis inG(i,j))

thenG(i,j)=G(i,j)+1;//G(i,j)存储每个网格内的点数目

endif;

Create density spread graph according toG;//绘制密度分布图

Store density valueskin threshold[];//确定密度阈值

return threshold;

end

其次, 对每个层次的阈值用等效规则计算不同的参数E[12], 伪代码如下：

procedure calculate_E(D)

begin

E=sqrt(MPts*V/(D*π));

returnE;

end

再次, 对每层阈值下的点进行聚类, 在原始DBSCAN基础上增加簇排序队列信息, 保证每次从队列中取出可达距离最小的样本点进行拓展, 从而减小初始参数选取对聚类结果的影响。算法的伪代码如下：

procedure queue_dbscan (U,D,MPts)

begin

for each unvisitedpinU

begin

Markpas visited;//将p标记为已访问

N=getNeighbours(p,E);

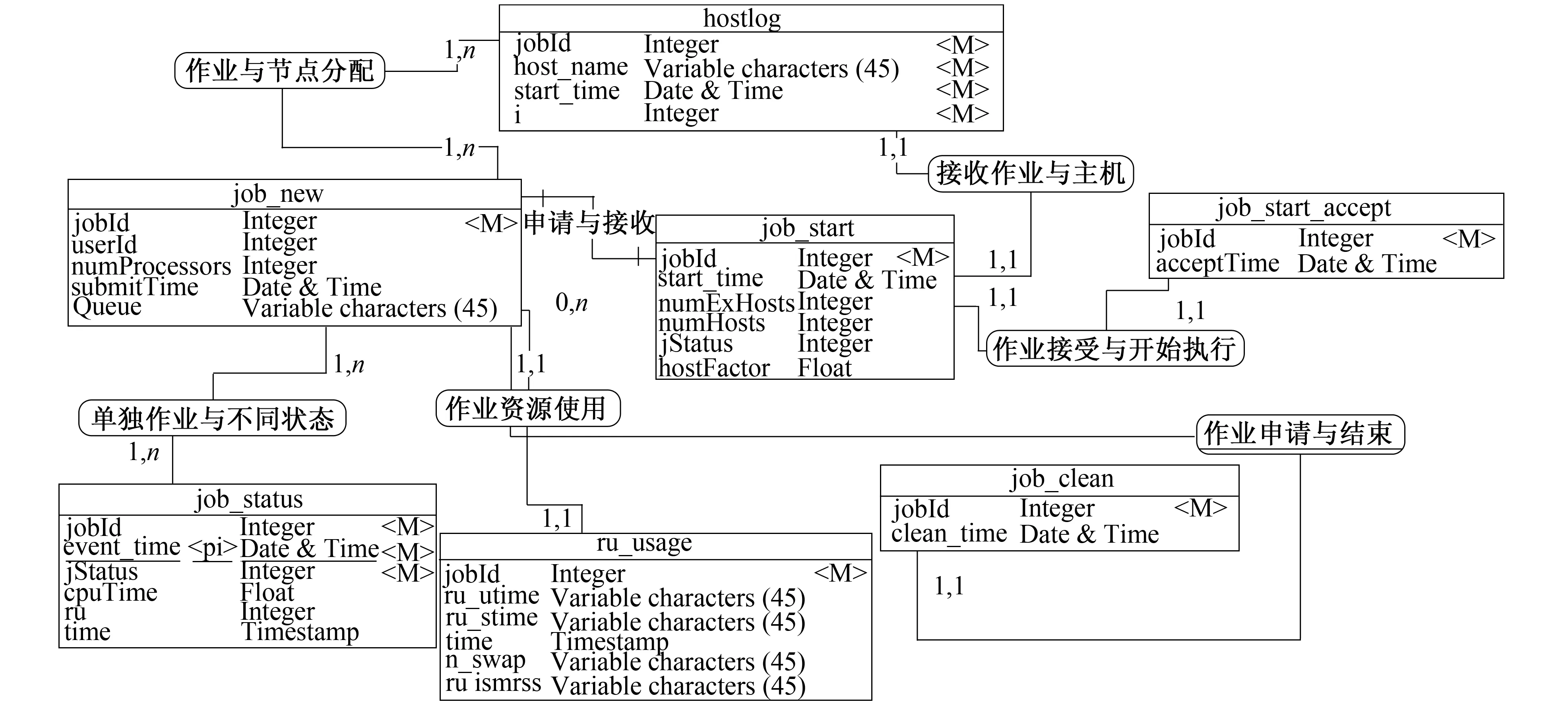
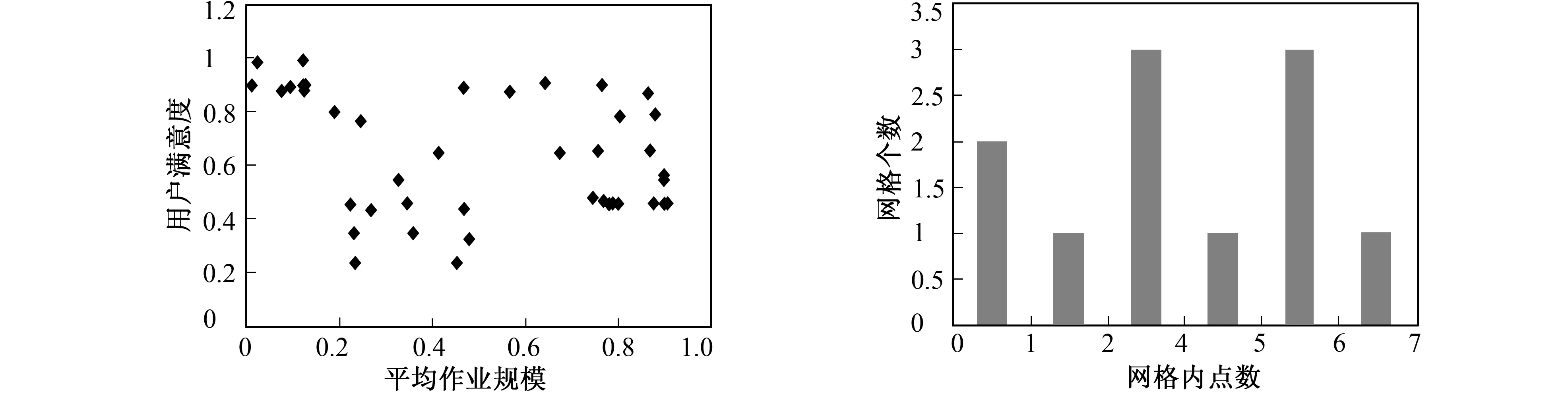
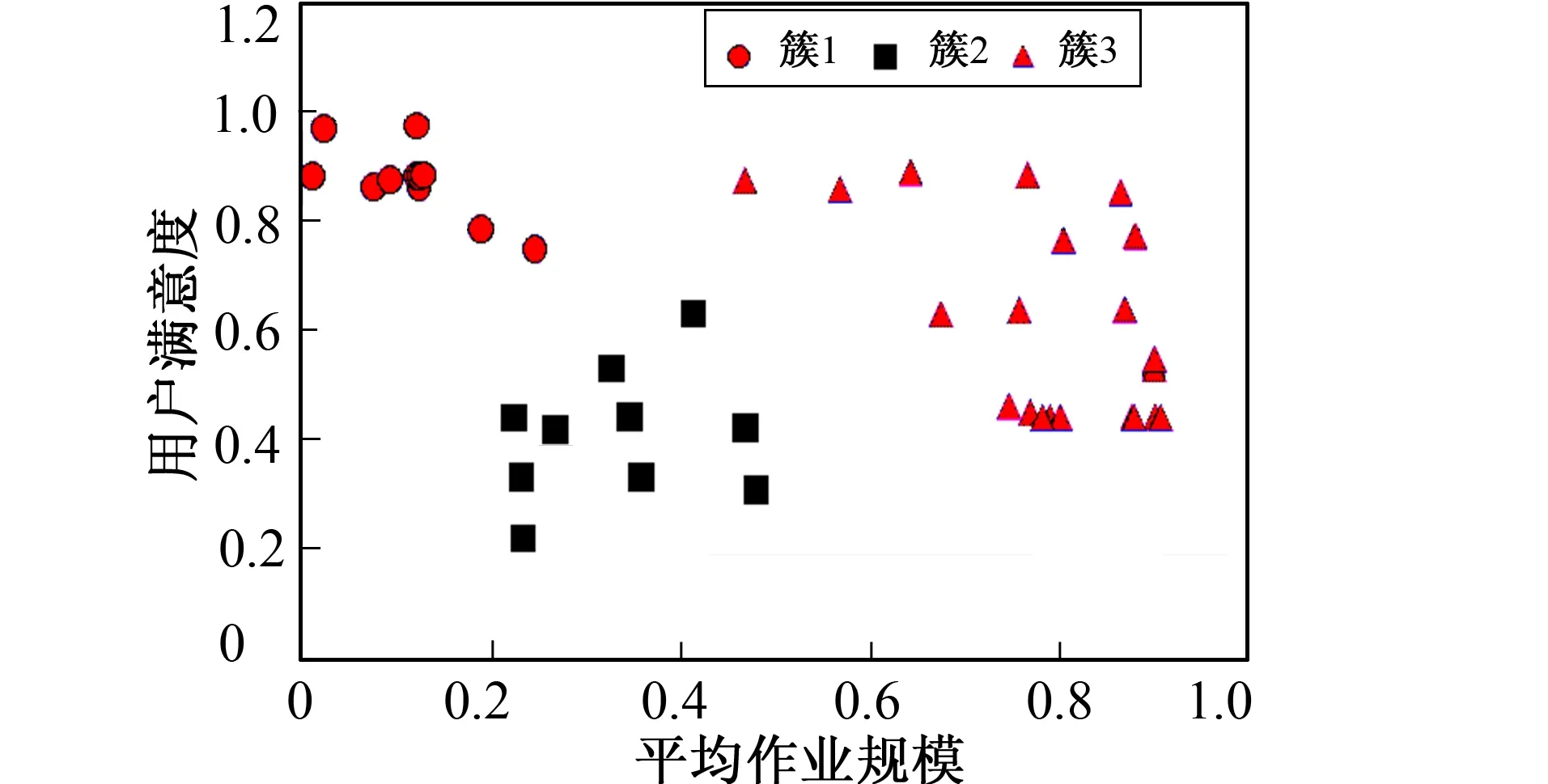
if sizeof(N)

then Markpas Noise;//将p标记为噪声

else

C=new cluster//建立新簇C

Addp(i) toR1//创建队列R1

Sort(R1)//将R1重新排序

Choose(p,R1)//在R1中选择距离最小的点

Save(p,R2)//将点保存至R2中

if(exists(p,R1)) then//若p已经存在

Instead(p,R1)//用新点代替旧点

Sort(R1)//将R1重新排序

endif

endif

endfor

end

最后算法的主调程序如下：

procedure QDBSCAN(U,MPts)

begin

threshold[]=threshold_value(U);

for each density valuekin threshold[]

begin

E=calculate_E(k);

G=units inUwhose points>k;

Find max unitUmaxinG;

queue_dbscan(Umax,k,MPts);

end

end for

end

4 算法在高性能计算中心用户数据的实例分析

该实验数据取自吉林大学高性能计算中心集群服务器的作业调度系统Platform LSF产生的日志lsb.events。日志信息由后台程序操作存入数据库中, 由应用程序完成数据统计。用户数据分析主要包括用户组成, 用户使用效果, 用户操作成熟度和用户占用资源分析等。相关数据包括作业成功率、 平均等待时间、 cpu利用率、 作业提交成功率、 使用天数、 作业规模和占用核心数等。

首先, 进行数据采集, 建立的数据库如图1所示。

图1 数据库E-R模型

其次, 对用户数据进行统计, 其统计项目如表1所示。

表1 用户数据统计表

再次, 将上一步所述数据进行归约和整理。即计算用户平均作业规模和用户满意度。平均作业规模使用平均消耗cpu时间进行度量

(3)

用户满意度使用作业成功率的正比例函数与平均队列等待时间的反比例函数的乘积表示

(4)

因此作业成功率越高, 平均等待时间越低, 则满意度越高。将式(3)、 式(4)结果归一化到[0,1], 并作为聚类分析的X和Y坐标。最终得到的数据集如表2所示。

表2 数据采集表

图2 数据网格划分 图3 密度分布图

然后, 对数据空间进行网格划分, 结果如图2所示。做出密度分布图, 结果如图3所示(B=0.025)。

可得到密度阈值分别为4和6, 根据等效原则[12]求出邻域半径

图4 聚类结果

最后, 依次使用阈值4和6, 根据改进聚类算法得出聚类结果如图4所示。

从聚类结果可看出, 用户分为3类。簇1代表的用户属于初级用户, 占用较少的集群资源, 有较好的满意度。簇2代表的用户属于中级用户, 该类用户占用一定集群资源, 但提交作业的效果并不理想。簇3属于高级用户, 该类用户相对于前两者占用较多的资源, 且在操作上较为成熟, 有较高的满意度。

算法分析的数据采集自中心试运行阶段, 用户数46, 作业样本数76 582。由于各位老师习惯于分享账号给自己课题组的学生用, 因此账号数较少, 实际使用人数在220人左右。从数据分析结果看, 簇1用户整体作业规模偏小, 平均等待时间较短, 提交作业成功率高, 运行成功率高, 具有较高满意度； 簇2用户作业规模中等, 处于常规调度排队中, 由于作业编写失误率偏高, 满意度偏低； 簇3用户属于集群大用户, 在调度策略中处于较高优先级, 通常该类用户在作业编写和运行方面较为谨慎, 所以有较高满意度。通过以上分析说明, 该实验的结果符合中心调度策略的调整, 具有准确性和可靠性。

实际对照用户信息, 簇1用户群体分为两部分： 一部分用户属于较成熟的用户, 以前使用过并行计算, 作业数据较简单, 倾向于做对比性测试, 在中心以试用资源为主, 实际提交的作业规模都偏小, 是中心的潜在客户群; 另一部分是在中心提交大量的单核作业, 计算时间较短, 但数量较大, 如生物类的基因比对等。这部分用户成熟度较高, 计算目的明确, 数据成熟, 是中心的重要用户群。簇2用户较多没接触过并行计算, 用户中初学者较多, 提交作业规模大且多, 作业数据不合理的偏多, 作业失败率偏高, 同时由于对用户控制了最大使用资源上限, 导致平均排队时间较长。根据反馈, 该类用户的意见较大, 需要进行针对性的技术培训, 加深对并行计算应用程序的了解, 以发展成簇3或簇1类的用户。簇3用户大都在校外租用过上海超算的计算资源, 有成熟的应用背景, 计算有明确的目的性, 是中心要优先保障和支持的客户群体。

改进后的算法与同类算法相比, 具有屏蔽输入参数变化的优点。在寻找下一个扩展点时, 其他同类算法采用随机选取, 忽略了已形成的簇本身带来的信息, 因此, 当输入参数产生细微变化时, 有可能导致输出点顺序上的很大改变。而本算法中利用了簇内部的信息, 因此降低了对参数的依赖, 使算法具有更高的可靠性。

5 结 语

笔者提出的DBSCAN改进算法, 在使用多密度阈值确定参数的基础上, 添加一个簇排序队列作为辅助工具, 更进一步减小初始参数选取对聚类结果的影响。实验结果表明, 改进的DBSCAN算法能较全面地对高性能计算中心的用户进行分类, 对调整调度策略, 提高集群使用效率等具有现实意义。

该实验的研究结果应用在集群作业调度方案调整中, 对不同类用户针对性地展开相关的技术培训, 提升用户体验； 关注簇2中用户作业提交失败原因并帮助其改善, 提高集群的有效资源使用效率, 从而从整体上提高集群的资源利用率。

参考文献：

[1]潘玲玲, 张育平, 徐涛. 核DBSCAN算法在民航客户细分中的应用 [J]. 计算机工程, 2012, 38(10): 70-73.

PAN Ling-ling, ZHANG Yu-ping, XU Tao. Nuclear DBSCAN Algorithm in the Application of Civil Aviation Customer Segmentation [J]. Computer Engineering, 2012, 38(10): 70-73.

[2]任鸿, 郑岩, 吴烨蓉. Clustering Analysis of Telecommunication Customers [J]. 中国邮电高校学报: 英文版, 2009, 16(2): 114-116.

REN Hong, ZHENG Yan, WU Hua-rong. Clustering Analysis of Telecommumication Customers [J]. China Post and Telecommunications University Journals: English Version, 2009, 16(2): 114-116.

[3]ESTER M, KRIEGEL H, SANDER J, et al. A Density-Based Algorithm for Discovering Cluster S in Large Spatial Databases with Noise [C]∥Proc of the 1996 2nd Int l Conf on Knowledge Discovery and Data Mining. Portland: AAAI Press, 1996: 226-231.

[4]蔡颖琨, 谢昆青, 马修军. 屏蔽了输入参数敏感性的DBSCAN改进算法 [J]. 北京大学学报, 2004, 40(3): 480-486.

CAI Ying-kun, XIE Kun-qing, MA Xiu-jun. Shielding the Input Parameter Sensitivity of the Improved Algorithm DBSCAN [J]. Journal of Peking University, 2004, 40(3): 480-486.

[5]于亚飞, 周爱武. 一种改进的DBSCAN密度算法 [J]. 计算机技术与发展, 2011, 21(2): 30-38.

YU Ya-fei, ZHOU Ai-wu. An Improved DBSCAN Algorithm Density [J]. Computer Technology and Development, 2011, 21(2): 30-38.

[6]武佳薇, 李雄飞, 孙涛, 等. 邻域平衡密度聚类算法 [J]. 计算机研究与发展, 2010, 47(6)： 1044-1052.

WU Jia-wei, LI Xiong-fei, SUN Tao, et al. Neighborhood Equilibrium Density Clustering Algorithm [J]. Journal of Computer Research and Development, 2010, 47(6): 1044-1052.

[7]王桂芝, 王广亮. 改进的快速DBSCAN算法 [J]. 计算机应用, 2009, 29(9): 2505-2508.

WANG Gui-zhi, WANG Guang-liang. Improved DBSCAN Algorithm Quickly [J]. Computer Application, 2009, 29(9): 2505-2508.

[8]高迪驹, 王天真, 刘洋, 等. 一种调整簇阈值的加速聚类分析算法及其应用 [J]. 数据采集与处理, 2012, 27(3): 278-293.

GAO Di-ju, WANG Tian-zhen, LIU Yang, et al. An Adjust Cluster Threshold Acceleration Clustering Analysis Algorithm and Its Application [J]. Data Acquisition and Processing, 2012, 27(3): 278-293.

[9]谭颖, 胡瑞飞, 殷国富. 多密度阈值的DBSCAN改进算法 [J]. 计算机应用, 2008, 28(3): 745-749.

TAN Ying, HU Rui-fei, YIN Guo-fu. Density Threshold Algorithm DBSCAN [J]. Computer Applications, 2008, 28(3): 745-749.

[10]马帅, 王滕蛟, 唐世渭, 等. 一种基于参考点和密度的快速聚类算法 [J]. 软件学报, 2003, 14(6):1089-1095.

MA Shuai,WANG Teng-jiao, TANG Shi-wei, et al. Based on a Reference Point and Density of Fast Clustering Algorithm [J]. Journal of Software, 2003, 14(6): 1089-1095.

[11]周水庚, 周傲英, 曹晶. 基于数据分区的DBSCAN算法 [J]. 计算机研究与发展, 2000, 37(10): 1154-1159.

ZHOU Shui-geng, ZHOU Ao-ying, CAO Jing. Based on Data Partition of DBSCAN Algorighm [J]. Computer Research and Development, 2000, 37(10): 1154-1159.

[12]HU Rui-fei, YIN Guo-fu, TAN Yin, et al. Cooperative Clustering Based on Grid and Density [J]. Chinese Journal of Mechanical Engineering, 2006, 19(4): 544-547.