锥面蝶簧式锁紧油缸中摩擦环的有限元分析

徐荣华，王卫英，樊金柱

（南京航空航天大学机电学院，江苏南京 210016）

0 引言

目前国内外，液压缸的自锁已逐渐脱离传统依靠封堵油路的方法来实现，转而改用依靠机械锁定的方式来实现［1］。锥面碟簧式锁紧缸就是一种新型依靠静摩擦力锁紧的液压缸，其结构简单合理，蝶簧能够产生足够的锁紧力在任意位置处长期锁紧，解锁可靠使用寿命长［2］。摩擦环是其关键技术之一，必须满足材料强度大小合适;若强度太小锁定吨位不够工程实用不大，强度过大将损坏关键零部件。

本文在锁紧缸的探讨过程中，发现锥面蝶簧式锁紧缸系列的摩擦环在有缺口结构下其锁紧吨位会得到很大提升，因此计划对现行锥面蝶簧式锁紧缸的摩擦环结构进行优化，在摩擦环总的缺口圆心角不变的条件下，改变摩擦环缺口的数量，同时为优化锁紧缸的体积，将摩擦环厚度由75mm优化为60mm。为验证这种改进方案的可行性，需要对摩擦环进行应力位移的分析与计算，为自锁油缸改进方案提供必要的理论依据。

1 锥面蝶簧式锁紧缸工作原理

锥面蝶簧式锁紧缸剖切结构简图如图1所示，摩擦环位于缸体左侧。显然，该装置的特点是结构简单能够无限地自动持续夹紧，并且锁紧吨位较大且无需单独的锁定和解锁回路。

图1 锁紧缸三维剖切装配简图

2 有限元模型的建立

2.1 装配体增量形式协调方程的建立

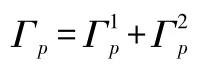
式中:uc及ur分别是可能接触面上节点和其他节点的位移向量。由式（1）的第2式可以得到

将式（2）代入式（1），可得凝聚后的方程为

便可得出两物体求解接触问题增量形式的广义协调方程:

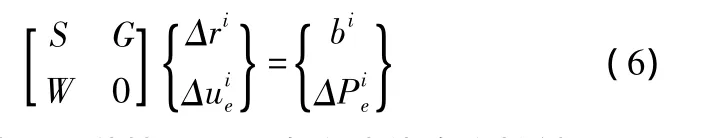
多块体接触分两种情况:1）多个块体多个接触面，2）单体有多个接触面。前者通常须处理刚体位移及接触面分布更复杂，而更具代表性。由此可获得与式（6）形式相同的增量形式的多块体接触广义协调方程。主要项S，G，W集成如下:

式中:S显然为对称矩阵，且当接触面较多时一般具有稀疏性。各分块矩阵正负号的判定在考虑从、主接触面及求解的接触力为作用于从接触面的作用力后得出［3］。

2.2 接触面条件的引入与求解

本文若将摩擦环作为单体零件计算，摩擦环在锁紧块滑槽中是轴向浮动的，难以定义其轴向约束，若在轴向不加约束，滑片可能会脱离锁紧块滑槽，就很难取得正确的分析结果。因此，如果取锁紧块、活塞、缸盖和摩擦环的装配图作为研究对象，那只需要对锁紧块进行约束即可，而锁紧块边界的确定比摩擦环要容易许多。

协调方程式（6）中有未知量，必须补充接触面条件迭代求解。本文所有零件均是对称接触，物理意义上要求接触的表面不会渗透，可传递法向压缩力和切向摩擦力，通常不传递法向拉伸力。因此，程序必须建立强制接触协调性。对于摩擦环与活塞杆，活塞与锁块之间均在有静摩擦力，Ansys Workbench中对于大变形问题的无摩擦或摩擦接触中使用增强拉格朗日公式法（Augmented Lagrange），增加了额外的控制自动减少了渗透。对于摩擦环与锁紧块，锁紧块与缸盖之间属于特定的“绑定”和“不分离”两个面间的接触类型，使用多点约束法（MPC），通过内部添加约束方程来“联接”接触面间的位移。如图2所示。

图2 Augmented Lagrange和MPC法示意图

前面是针对法向接触的，本文零件间有摩擦力，还须定义切线方向接触，可利用罚函数算法求解。对于法向刚度，这是一个相对因子，一般变形问题使用1.0，接触刚度在求解中可自动调整，如果收敛困难，刚度自动减小［4］。

2.3 有限元模型的建立和加载

对应装配体材料参数如表1所示。采用SOLID185单元，对三维模型进行网格划分，有限元模型如图3所示。

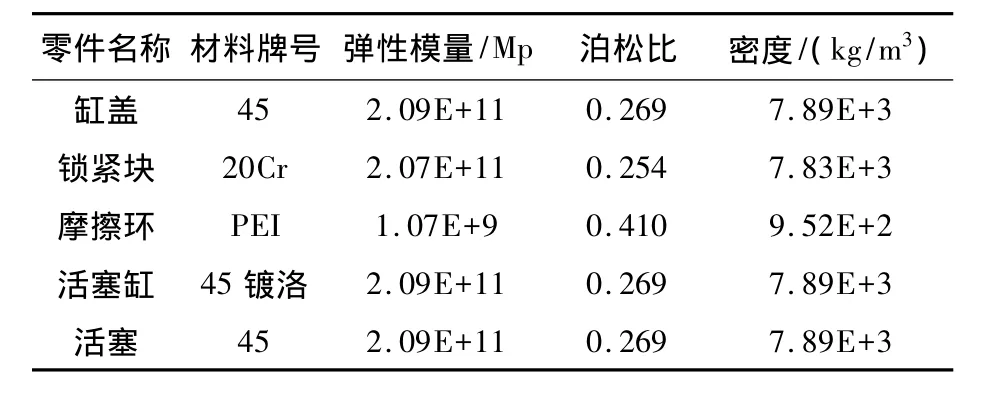
表1 零部件相关参数

图3 有限元网格模型

对于分析摩擦环横向应变与应力，可以对受力做适当简化:摩擦环所受纵向力及端盖对摩擦环头部的支反力可忽略;只考虑横向压力即可。对装配体施加对称约束，采用TARGET170目标单元和八节点高阶四边形单元CONTACT174来模拟摩擦环跟活塞杆的接触，接触面间的摩擦系数取0.03。

3 计算结果分析与结论

在锥面蝶簧式锁紧缸实际锁紧工况下，对于d100的活塞杆蝶簧推力一般为12t，解锁压强最大120Mp，活塞杆与水平面垂直由于摩擦环缺口圆心角之和是24°，所以增加摩擦环等分结构就相应减小了单个缺口圆心角的度数，那么不同缺口下摩擦环有限元计算结果如表2所示。通过有限元的分析，可以得出以下结论:

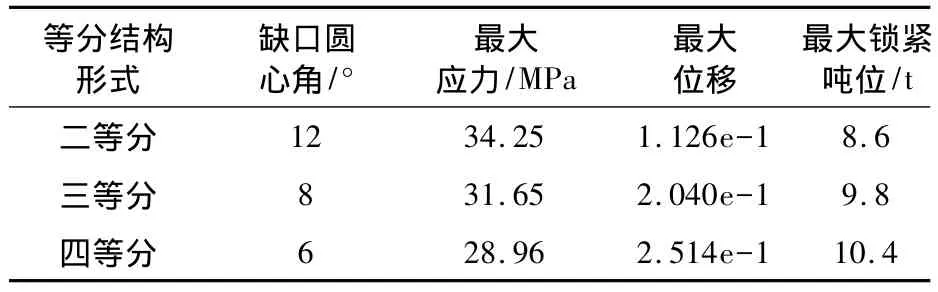
表2 不同缺口下摩擦环应力、位移、锁紧吨位计算结果

1）通过对装配体有限元的分析（见图4）可知模型最大变形1.236e-1mm，保持锁定。通过有限元模型多次迭代求解结果收敛图（图5）可知，锁紧吨位基本收敛，有限元分析基本正确。

图4 四等分组件位移应力云图

图5 有限元模型多次迭代求解结果收敛图

2）通过有限元的分析可知模型的最大应力位置出现在摩擦环底部与锁紧块接触的部位，与活塞与摩擦环锥面结构相吻合（见图6和图7）。

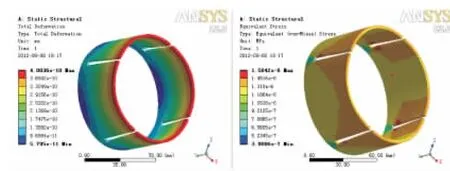
图6 四等分摩擦环位移应力云图

3）在大吨位锁定条件下，将锁紧缸摩擦环二等分结构增加为四等分结构后，摩擦环缺口圆心角加大，摩擦环长度从75mm减为60mm后，锁紧缸体积变得更小，在这两个因素的作用下，导致摩擦环最大应力从34.25MPa减小到28.96MPa，锁紧吨位从8.6t幅增大到10.4t。

图7 四等分结构摩擦环1/4片的位移应力云图

4）通过对锥面蝶簧式锁紧缸摩擦环的研究表明，在摩擦环四等分的情况下数值计算和实际试验吻合较好，在其余等分结构虽然没有试验数据验证，但也符合锁紧缸的锁定特性。可以为锥面蝶簧式锁紧缸吨位锁定设计提供一种方法。

4 结语

通过对锥面蝶簧式锁紧缸摩擦环进行有限元分析，构造特定装配体网格拓扑结构，使用分块结构化网格对该模型进行有限元模拟，四等分式的摩擦环结构优化，降低了对锁紧力的要求，扩大了选材范围，大吨位的锁定更是提高了锁紧缸的工程实践应用，为锥面碟簧式锁紧缸的设计改进提供了新的分析方法。

［1］邹建华，吴榕.液压锁技术现状分析［J］.机械工程与自动化，2007（5）:184-188.

［2］王长征，鲁腊福.锥环-蝶簧式锁紧液压缸锁紧力研究［J］.液压与气动，2011（4）:84-86.

［3］姜育松，苏超.多物体接触有限元法及其对围岩的模拟［J］.岩土力学，2011，32（11）:104-108.

［4］孙文理.有限元分析后处理中应力与位移显示的算法［J］.哈尔滨理工大学学报，2005（5）:77-78.