基于Pro/E与ANSYS的减速箱齿轮模态分析

周建钊，徐肖攀，储伟俊

（中国人民解放军理工大学工程兵工程学院，江苏南京 210007）

0 引言

机械振动是机械动力学研究的重点问题，也是工程结构设计必须考虑的问题。在机械行业的诸多领域都会见到大量的旋转结构，这些结构在整个工程机械中占有极高的比重。共振引起的较大激振应力，以及复杂的外界激振力相互作用，是导致绝大部分旋转体损坏、报废的主要原因［1］。模态分析适用于研究结构振动特性，即固有频率和振型、振型参与系数等［2］。它能使结构设计有效地规避共振，有助于在其他动力学分析中估算求解控制参数［3］。近些年很多学者致力于“动态设计”研究。根据机械振动理论，借助“有限元法”、“传递矩阵法”、“试验模态法”、“混合建模法”、“人工神经网络理论”等建模方法对机构进行动态优化，取得了很多成果［4］。但是，由于所研究的问题大都比较复杂，动态设计至今还没有一套完整的理论。本文将根据工程动力学理论，通过对 Pro/E、ANSYS结合使用，研究齿轮振动特性。

1 减速箱齿轮振动分析

齿轮是减速箱（或减速器）的重要组成部分，它在高速转动中的动态性能是评价减速箱整体性能优劣的主要依据［5-6］。在啮合过程中，齿轮副因受到周期性冲击载荷作用而产生振动，其中的高频分量为齿轮的固有频率［7］。影响齿轮副振动频率的因素很多，主要包括:轮齿刚度、轴的刚度、齿轮副尺寸、润滑油膜厚度，以及各种阻尼等。根据公式:

可得固有频率的理论值。其中，m、k分别为齿轮的等效质量和等效刚度。为了避免机构运行时产生共振，必须准确测定齿轮的固有频率，使外加激励远离这些固有频率点［6］。

2 模态分析

根据工程动力学中模态分析理论以及弹性力学有限元法，［8］可得齿轮系统微分方程:

其中:{X}={x1，x2，…，xn}T表示节点位移列向量，{}，{}分别表示结构的加速度、速度向量;［M］，［C］，［K］分别表示质量矩阵、阻尼矩阵和刚度矩阵;{f（t）}={f1，f2，…，fn}T表示外加的激振力向量。

由于着重研究齿轮自由振动特性，因此可设外加激振力{f（t）}为零，从而得到自由振动方程。由于阻尼对齿轮振动的影响很小可以忽略，即令［C］=0，从而得到无阻尼自由振动方程:

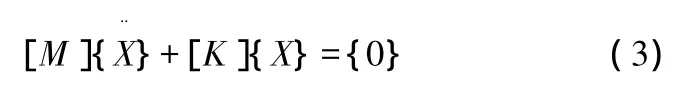
设结构作如下简谐振动

将式（4）代入式（3）可得齐次方程:

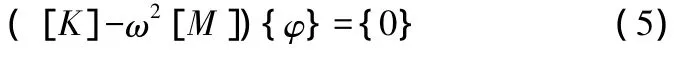
实际中，齿轮各节点振幅φ{}不可能全为零，因此（［K］-ω2［M］）的行列式为零是式（5）成立的充要条件［9］，即:

由于［K］与［M］均为n阶方阵，则式（6）是关于ω2的n次代数方程，最终能够得到n阶固有频率ωi（i=1，2，3，…，n）。将ωi代入式（5）可得到一个列向量{φ}i=（φi1，φi2，φi3，…，φin），即为振型或模态。因此，通过求解式（6）、式（5）便可求得齿轮的各阶固有频率和振型。

3 三维建模与实体分析

3.1 基于Pro/E建立齿轮三维实体模型

根据特定工程结构要求，齿轮的相关数据如下:齿顶直径48mm，齿底直径40mm，齿厚16mm，中间壁厚 6mm，沉槽直径32mm，中间通孔直径16mm，齿数为10，材料密度ρ=7.8×103kg/m3，弹性模量E=2.06×1011Pa，泊松比为0.28。通过Pro/E进行减速箱齿轮三维实体模型构建，如图1（a）所示。

图1 Pro/E实体模型与ANSYS网格划分

3.2 利用ANSYS进行齿轮模态分析

利用ANSYS的模型导入功能，将Pro/E中构建的三维模型导入ANSYS工作界面，对其进行网格划分、定义约束，求解固有频率及振动模态，如图1（b）所示。

在进行齿轮固有频率求解过程中，首先定义单元属性。本课题所选用的单元是Solid Brick 186，每个单元有20个节点，能够使计算结果比较准确。之后，定义材料属性。在Material props中定义弹性模量、泊松比、材料密度等值。然后，进行网格划分。将Mesh tool选项卡中的Smart size勾选，并将数值设置为3然后进行网格划分。之后，定义约束。选择D16轴孔内壁为约束面，约束方向选择All DOF。然后，设置模态求解参数。打开模态求解选项卡，定义要求解的模态数（这里输入15，进行前15阶模态分析），再定义振动频率范围（取0～10000Hz）。输出控制部分设定为All Item，采用每一子步频率输出。以上过程完成后便可进行求解，求解的结果在General postproc选项卡中查看。

3.3 频率及模态分析结果与讨论

对齿轮进行模态分析，一般而言，阶数越低，齿轮振动对系统的影响越大，一般提取前5-10阶固有频率和振型即能满足精度要求［9］。在本课题中，运用Block Lanczos法设定模态提取阶数为15阶，这样既能得出对齿轮影响较大的固有频率和振型值，又能加快求解速度。得到的前15阶固有频率、振型描述以及最大振幅等数据，在表1中详细列出。

表1 减速箱齿轮前15阶固有频率和振型描述

1-3阶固有频率对应的振型如图2所示。当频率在6.6382Hz、6.6386Hz、8.8424Hz时，齿轮变形量相对较小。图中虚线表示齿轮未变形的轮廓线，实体部分是变形后的形状。1，2阶固有频率下，齿轮分别绕y，x轴弯曲振动;3阶固有频率下，齿轮沿yoz平面对折振动，振型比较复杂。

图2 齿轮在1－3阶频率下的模态振型

9-12阶固有频率下的振型如图3所示。当频率在25.372～36.465Hz之间变化时，最大变形量相对较小。因此，当外加激振力的频率在0～8.8424Hz与25.371～ 36.465Hz之间时，齿轮传动系不易产生共振。9，10阶固有频率下，齿轮分别绕x，y轴作弯曲振动，最大振幅均出现在齿顶处;11，12阶固有频率下，齿轮均作圆周振动，通过动画模拟可知最大振幅在齿顶与齿根之间交替出现。

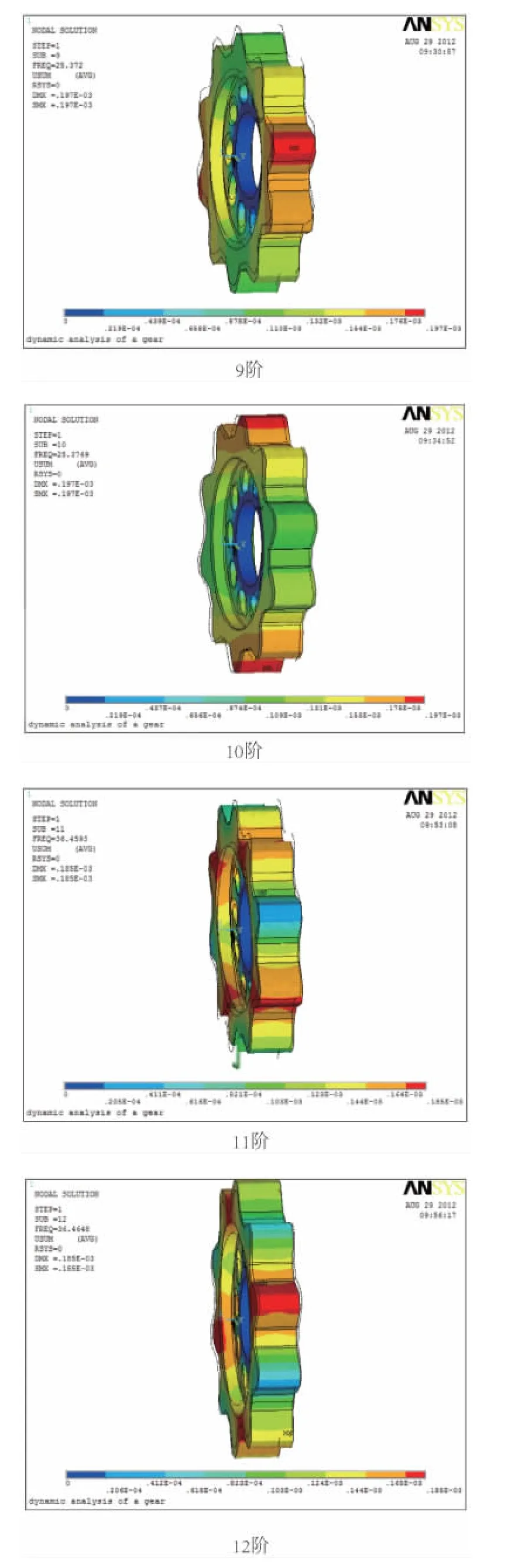
图3 齿轮在9－12阶频率下的模态振型

从4-8、13-15阶固有频率对应的振型可知:当频率为ω6=11.174Hz时，齿轮的振幅最小，形变均匀;当频率为第7，8，13阶固有频率时，齿轮振幅较大，形变程度大，振动剧烈;当频率为ω14=41.467Hz时，齿轮振幅最大，形变量也最大，沿yoz平面内3阶弯曲振动;当频率为ω15=41.467Hz时，齿轮作伞状振动，轮齿形变非常明显。因此，在设计与其相啮合的齿轮减速系统时，箱体的振动频率、轴的挠动频率以及轮齿啮合时的冲击频率应该尽量避开41.467Hz，以免产生剧烈共振。图4为4-8、13-15阶模态振型

图4 4－8、13－15 阶模态振型

von Mises等效应力分布云图如图5所示。从中可以看出:最大应力分布于齿轮台阶孔边缘，大小为5.79MPa;最小应力分布于轮齿上，大小为0.229MPa。因此，齿轮台阶孔应力集中。为减小应力集中，可以对齿轮台阶壁进行加厚处理，同时增大内壁与台阶孔间过渡圆弧半径，以减小结构突变引起的应力分布不均。

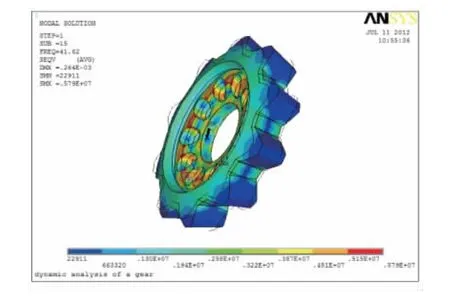
图5 von Mises等效应力云图

4 结语

1）将Pro/E、ANSYS软件相结合，对齿轮进行三维实体建模、有限元建模以及模态分析。这种综合运用不同软件对实体进行动力学分析的方法，克服了单一软件在建模速度、单元划分效果以及求解速度等方面的不足，一定程度上提高了CAE分析的效率，具有一定的通用性。

2）利用ANSYS对齿轮进行模态分析，得到前15阶固有频率以及相应的主振型，并在此基础上分析了齿轮的变形特点和von Mises等效应力分布状况，为齿轮结构分析与合理设计提供了一种范例，具有一定的借鉴意义。

［1］葛正浩，翟志恒，姚卫民，等.基于ANSYS的渐开线齿轮模态分析与研究［J］.陕西理工大学，2011，29（6）:51-55.

［2］舒彪，喻道远，王灯，等.采用 UG、HyperMesh和 ANSYS的齿轮轴模态分析［J］.现代制造工程，2012（2）:71-73.

［3］张梅军，曹琴.工程机械动力学［M］.北京:国防工业出版社，2012.

［4］张志强，郭京波.机械动态优化设计综述［J］.石家庄铁道学院学报，2005，18（1）:74-76.

［5］孙辉，高强.弧齿锥齿轮的模态分析［J］.苏州大学学报（工科版），2011，31（1）:36-38.

［6］王磊，练章华，阳星，等.基于ANSYS的钻柱扭镇模态分析［J］.石油机械，2012，40（2）:4-6.

［7］孙恒，陈作模，葛文杰.机械原理［M］.北京:高等教育出版社，2006.

［8］王勖成.有限单元法［M］.北京:清华大学出版社，2003.

［9］李健，戚晖，赵玉良，等.基于ANSYS技术的主从控制机械臂支承架模态分析及优化［J］.制造业自动化，2011，33（6）:12-15.