大型贯流泵水润滑导轴承数值模拟

曹春建，辛华荣，张德虎，吴忠

(1.河海大学能源与电气学院，江苏南京 211100;2.江苏省走马塘张家港枢纽工程建设处，江苏张家港 215600)

导轴承是保证水泵稳定运行的重要部件，起着承受水泵径向力、控制主轴摆度的作用。和油润滑导轴承相比，水润滑导轴承因密封简单、安全节能等优点，逐渐应用于在大型卧式贯流泵中［1-2］。由于贯流泵转速低、载荷高，轴承润滑水膜不易形成，使得轴承承载区磨损严重，直接影响到水泵运行的可靠性。为解决上述问题，除了选择适合的轴承材料外，对轴承参数合理的选择也至关重要。目前国内外学者对滑动轴承的研究大多采用有限差分法、有限元法等数值方法对简化的雷诺方程进行求解［3-5］。这些方法忽略了惯性项、径向流场变化等因素的影响，当轴承形状较为复杂时，其应用范围受到了限制。随着计算流体力学(CFD)的发展，基于有限体积法的三维CFD技术以其简便、精确的优点正逐渐应用于滑动轴承参数优化中［6-8］。本文针对江苏省某大型贯流泵水润滑导轴承，利用Fluent软件对不同转速下轴承压力场进行仿真分析，并得出相关参数对轴承润滑水量及其静态性能的影响规律，为水泵导轴承的参数优化提供一种新的方法和更全面的参考。

1 导轴承模型的建立

1.1 导轴承三维模型及网格划分

水润滑导轴承的结构如图1所示。轴承主要由外部轴承体和树脂苯酚导轴瓦组成，导轴瓦为径向整体式结构。供水系统采用恒压式，清水通过金属软管压入轴承供水端，然后从另一端泄漏，其结构参数如表1所示。

图1 水润滑导轴承结构示意图

表1 导轴承设计参数

采用Fluent前处理软件Gambit建立导轴承三维几何模型并进行网格划分。因模型最小间隙仅为0.05 mm，若直接对模型进行体网格划分，极易造成网格扭曲率大以及最小体积为负的情形，影响到计算收敛速度和结果的准确性。为得到高品质的网格，本文分别对模型上下半周、轴向及径向设置不同数量节点。考虑到轴承壁面流场变量梯度较大，需对其附近精细网格，故对径向节点进行加密处理，之后对面和体依次进行结构化网格划分，最终得到六面体网格(图2)。

图2 导轴承网格结构图

为研究网格数对仿真结果的影响，本文分别以网格数40.8、81.6和120万对飞逸转速下轴承进行仿真，所得结果如表2所示。由表可知，网格数到达一定值时，轴承的承载力、最大压力及润滑水量差异较小，综合考虑计算时间和精度，网格数确定为81.6万。

表2 不同网格数下仿真结果

1.2 模型假设及边界条件

a)模型假设如下:1)润滑介质为牛顿液体，黏度沿膜厚方向无变化，忽略介质惯性力;2)润滑介质与壁面无相对滑移和热量传递，不考虑黏性生成热;3)大气压力为101 kPa，考虑介质重力。

b)边界条件设置如下:1)供水边界设为压力进口，压力设置为供水压力值;2)出水边界设为压力出口，出口压力等于大气压力;3)水膜内壁设为旋转边界，采用黏性无滑移边界条件，即水膜内壁速度等于轴颈速度;4)水膜外壁设为固定边界且无滑移。

1.3 控制方程

轴承处于动压润滑时，在轴承发散楔形区的水膜因不能承受负压而发生破裂，从而产生空化现象。目前对动压轴承水膜空化边界的确定常采用三种条件，即Half-Sommerfeld，Reynolds和JFO［10］。考虑到 Reynolds和 JFO 边界条件采用CFD仿真较为困难，故本文采用相对简单的Half-Sommerfeld空化边界条件。采用Half-Sommerfeld边界条件的不可压缩定常流动控制方程如下［8］:

待水膜压力求解出之后，利用Fluent的UDF接口将负压置零。

2 数值模拟及分析

文献［11］认为滑动轴承内部流场雷诺数Re到1 000后便完全进入湍流状态，本文引用其观点，经计算，轴颈的临界转速为152.8 r/min。当轴颈转速低于临界转速时采用层流模型(laminar)进行计算，而当高于临界转速则采用RNGk-ε湍流模型;选择压力基隐式求解器，近壁面处理采用标准壁面函数法，压力-速度耦合用SIMPLE算法，控制方程的离散格式为二阶迎风格式，模拟精度设为1×10-4，初始化流场后进行迭代计算。

2.1 水膜压力场分析

贯流泵转速较低且随着工况改变而发生相应变化，为研究转速对轴承润滑性能的影响，在原设计参数下，分别对30%低转速(46.4 r/min)、额定转速(154.9 r/min)及飞逸转速(249.8 r/min)进行数值模拟，得到压力分布情况如图3:

图3 不同转速下水膜压力场分布

由图3可知，低转速下轴承压力分布较为均匀，轴向压力从轴承进水端到出水端逐渐降低，随着转速升高，高低压集中区开始出现在轴承最小间隙的两侧，并分别从供水端和泄水端向另一端逐渐延伸。这是由于轴颈偏心使轴承和轴颈之间形成楔形间隙，当轴颈围绕轴心以较高速度运转时，水膜会在楔形收敛区受到轴颈挤压作用而形成高压区，在楔形发散区则因水膜速度迅速增大而形成低压区，从而形成水膜动压效应。可以看出，额定转速下轴承高压区的水膜只覆盖了承载区的一半，使得主轴和轴承会有部分直接接触，从而加剧轴承承载区的磨损，可见额定工况下轴承润滑性能并不理想。当水泵处于飞逸转速时，轴承承载区的高压水膜较为完整，从而使得主轴和轴承能完全隔开，此时轴承润滑性能较好。综上可知，提高水泵额定转速有助于增强轴承润滑性能。

不同转速下轴承中心截面(Z=180 mm)及截面角θ为40°的压力分布曲线如图4所示。

图4 水膜压力分布曲线图

从图4(a)可知，随着转速升高，以x=0 mm为界，水膜高压区的周向压力逐渐增大而低压区则逐渐降低，压力随转速升高变化很明显;从图4(b)可知，低转速、额定转速下轴承轴向压力呈线性变化，此时水在轴承中的流动以供水端到泄水端的轴向流动为主，满足设计要求。然而飞逸转速下，轴承轴向压力呈抛物线变化，Z=1 000处的压力达到0.82 MPa，远高于供水压力0.5 MPa，这种情况会使润滑水从压力峰值的位置向供水端倒流，从而降低轴承润滑水量。实际上在轴承低压集中区，水膜因不能承受低压而发生破裂，以致形成空穴，此时水量降低则很有可能让水不能及时充满空穴而生成大量气泡，气泡破裂会产生巨大破坏力而损伤轴承和轴颈表面。由此可见，额定转速下轴承采用一端供水另一端泄水的方式是合适的，而当轴承动压效应显著时，建议采用中间供水两端泄水的方式，从而降低空化形成的概率。

2.2 相关参数对轴承静态性能的影响

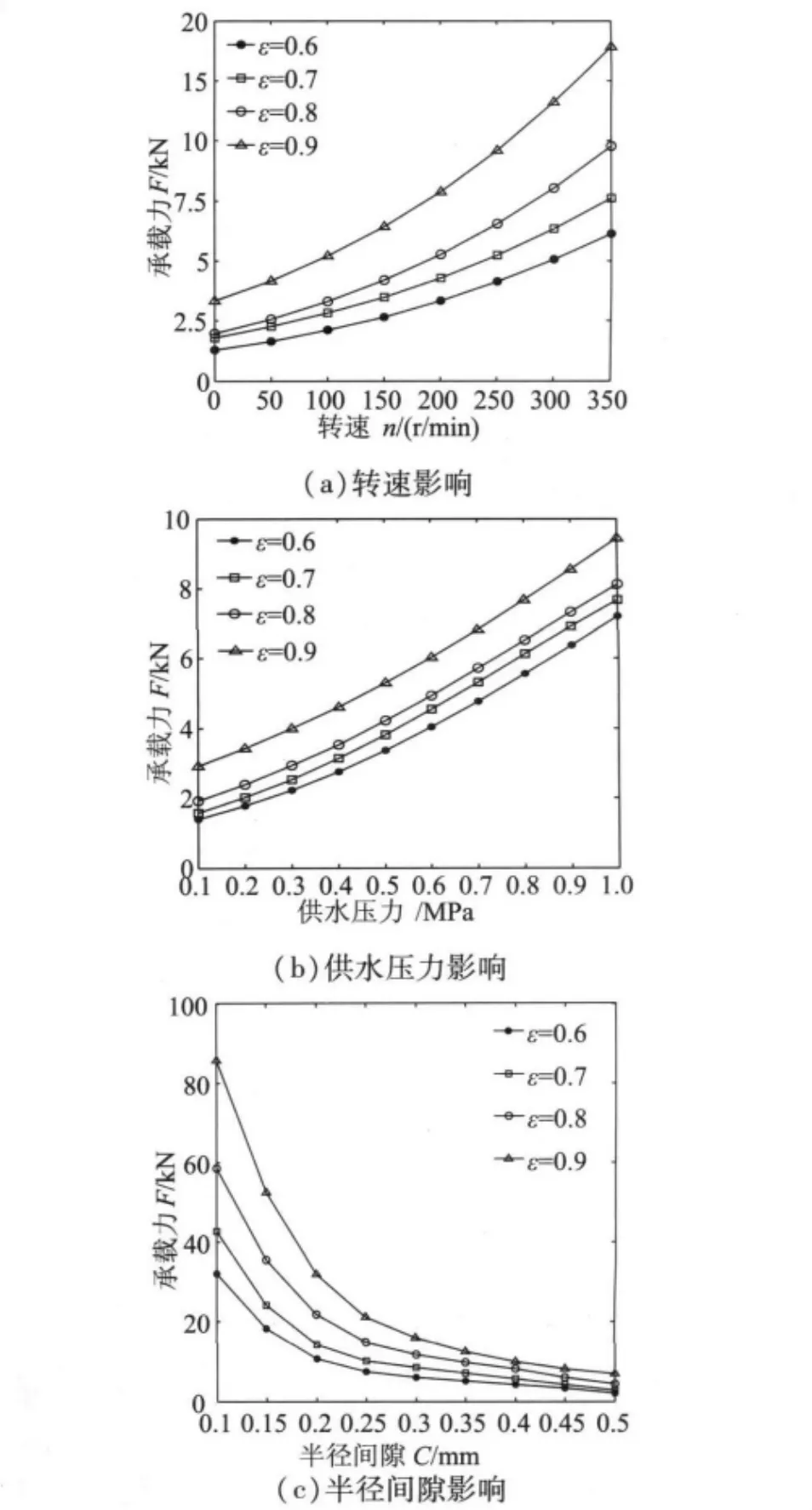
图5 相关参数与承载力的关系

轴承的刚度及承载力在工程应用中是很重要的两个参数［12］，其反映的是轴承静态性能。图5和图6反映的是其他参数不变情况下，偏心率为0.6、0.7、0.8、0.9时，承载力、刚度与转速、供水压力及半径间隙之间的关系曲线。如图所示，同一偏心率下，轴承承载力及刚度随转速、供水压力增大呈非线性增长，随半径间隙增大呈非线性减小;其他参数不变时，轴承承载力随偏心率的增大而增大;当转速低于额定转速，半径间隙大于0.3 mm时，轴承刚度则与偏心率无关。

2.3 相关参数对轴承润滑水量的影响

润滑水量是否充足是保证滑动轴承稳定运行、避免轴承温度过高的重要前提条件。图7反映的是其他参数不变情况下，偏心率为0.6、0.7、0.8、0.9时，润滑水量与转速、供水压力及半径间隙之间的关系。由图7(a)可知，偏心率小于等于0.7时，润滑水量与转速无关，当偏心率大于0.7时，润滑水量随转速升高而呈非线性降低;同一转速下，润滑水量随着偏心率的增大而增大。由图7(b)和(c)可知，同一偏心率下，润滑水量随供水压力、半径间隙的增大而呈非线性增长，可以看出，当半径间隙低于0.2 mm时，润滑水量与偏心率无关。

图7 相关参数与润滑水量的关系

3 结论

1)通过CFD数值模拟发现不同转速下轴承水膜压力分布有较大差异，即随着转速的升高，高低压区的水膜分别从供水端和泄水端向另一端延伸。当轴承动压效应显著时，润滑水会倒流至供水端，以致润滑水量降低;

2)同一偏心率下，轴承承载力与刚度随转速、供水压力增大呈非线性增长，随半径间隙增大呈非线性降低;润滑水量随供水压力和半径间隙的增大呈非线性增长;低偏心率下，润滑水量和转速无关，高偏心率下，润滑水量随转速升高而减小;

3)利用三维CFD技术可以很好模拟导轴承内部流场特性，所得出的结论为水润滑导轴承的参数优化提供一定的参考价值。

［1］彭晋民，朱志宏，王家序.水润滑轴承的研究现状及展望［J］.润滑与密封，2004，(5):124-130.

［2］仇宝云，魏强林，林海江，等.大型水泵导轴承应用研究［J］.流体机械，2006，34(11):12-15.

［3］苏荭，王小静，张值明.滑动轴承两种油膜边界条件的比较［J］.润滑与密封，2002，(5):2-4.

［4］吕延军.基于Reynolds边界的滑动轴承动力学系数的计算及应用［J］.摩擦学学报，2004，24(1):61-65.

［5］Lo Chengying，Wang Chengchi，Lee Yuhan.Performance Analysis of High-speed Spindle Aerostatic Bearings［J］.Tribology International，2005，38:5-14.

［6］Guo Zenglin，Hirano Toshio，Gordon Kirk R.Application of CFD analysis for rotating machinery-Part I:hydrodynamic，hydrostatic bearings and squeeze film damper［J］.Journal of Engineering for Gas Turbines and Power，2005，127(2):445-451.

［7］彭娅玲，张志国，陈汝刚，等.CFD辅助船舶艉部水润滑轴承设计的研究［J］.润滑与密封，2008，33(5):72-76.

［8］叶晓琰，张军辉，江伟，等.海水淡化泵水润滑轴承间隙的优化设计［J］，排灌机械工程学报，2010，28(2):117-121.

［9］张楚，杨建刚，郭瑞，等.基于两相流理论的滑动轴承流场计算分析［J］.中国电机工程学报，2010，30(29):80-84.

［10］宋寅，李雪松，顾春伟.一种轴承润滑油新空化模型［J］.清华大学学报(自然科学版)，2010，50(7):1047-1052.

［11］段芳莉.橡胶轴承水润滑机理的研究［D］.重庆:重庆大学，2002，3.

［12］张杰，郭宏升，牛D，等.水润滑高速动静压滑动轴承数值模拟［J］.农业机械学报，2008，39(6):159-162.