柔性管Reel-lay铺管安装稳定性分析
白 勇,唐继蔚,余彬彬,阮伟东,闫会宾
(1.哈尔滨工程大学船舶工程学院,黑龙江哈尔滨 150001;2.浙江大学建工学院,浙江杭州 310058)
柔性复合管是由不同种材料构成的管壁层复合而成的,有相对较低的轴向弯曲刚度[1]。这里研究的柔性管是纤维增强热塑性塑料复合管,其为一种高压塑料复合管,由三层材料构成,内层为PE100,外层为PE80,中间层则是增强材料复合而成的增强带,增强材料可以是聚酯纤维、芳纶纤维或钢丝等,如图1所示[2]。在柔性管安装分析过程中,有以下几点需要注意:其一是管道的轴向刚度和弯曲刚度,因为柔性管材料为复合材料且弹性模量较小,安装过程中柔性管所能承受轴向载荷和弯曲载荷有限;其二是管道的浮重,由于柔性管质量比较小,安装时需要附加配重以满足管道的安装稳性和在位稳定性。
近几十年来很多人为管道安装分析和改进做出了极大贡献。Dixon和Rutledge用奇异摄动法分析了JLay铺管法[3];Gu和Gong通过大量敏感性分析进一步研究阐述了S-lay铺管法[4-6];Lenci和Callegari提出了多个静态J-lay铺管法的理论计算模型[7];Wang在J-lay和S-lay铺管数值模型中考虑了水流作用[8-9];Szczotka运用了刚性有限元法解决J-lay铺管问题并与ANSYS分析结果进行了比较等[10]。以上研究主要针对静态环境下钢管的铺设分析,这里分别通过理论分析和有限元模拟用Reel-lay铺管法铺设柔性管来研究其在不同条件、载荷和环境作用下的稳定性问题。
1 柔性管属性
在做安装分析之前,必须知道柔性管的截面属性,包括拉伸性能和弯曲性能。通过在有限元软件ABAQUS中建立局部管段模型来获取管道力学性能,具体可参考文献[12],柔性管具体参数见表1,与钢管大不相同:柔性管的拉伸刚度和弯曲刚度都比钢管小很多,并呈现出非线性的特点,如图2、3所示。

图1 柔性管结构示意Fig.1 Construction of flexible pipe

表1 柔性管参数[12]Tab.1 Parameters of flexible pipe

图2 柔性管轴向拉力-应变曲线[11]Fig.2 Axial loading behavior of flexible pipe

图3 柔性管弯矩-曲率曲线[12]Fig.3 Bending loading behavior of flexible pipe
2 载荷及控制方程
图4为典型的Reel-lay铺管,在研究柔性管水下部分平面内稳定整体稳定性问题时,可以将管道分为两个部分:
1)悬浮段,从顶部脱离点(TOP)到触地点(TDP)之间的管段;2)触地段,管道触地点(TDP)之后置于海床上的部分。
2.1 悬浮段
在悬浮段的管道曲率主要由船上张紧器提供的顶部拉力、船舶的运动、波浪载荷、水流载荷等控制,当外部载荷过大将会导致管道在铺设过程中弯矩突然增大引起管道局部屈曲或坍塌破坏。
悬浮段的柔性管主要受到顶部拉力、水流载荷。如图5所示,将悬浮段划分成多个微小管段并建立相应的局部坐标系,通过微段受力平衡得到:
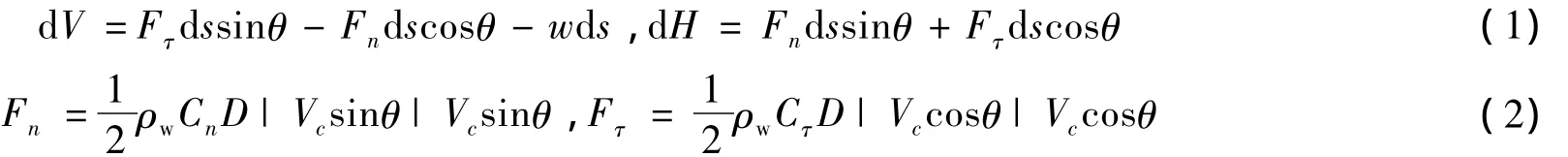
式中:dV,dH分别为管段在垂直和水平方向上的增量;Fn,Fτ分别是作用在管段上的水动力在垂直和切向方向上的分力;Cn,Cτ为水动力系数;ρw为海水密度;D为管段外直径;w为管道单位长度的浮重;Vc为水流速度;ds为管段长度;θ为管段与水平方向的夹角。

图4 柔性管Reel-lay铺管法示意Fig.4 Configuration of flexible pipe by Reel-lay method
对悬浮段柔性管而言弯曲刚度对整管的影响十分复杂,但由于管道很长且柔性管的弯曲刚度较小,所以这部分的影响可以忽略。根据力与θ角度的关系:
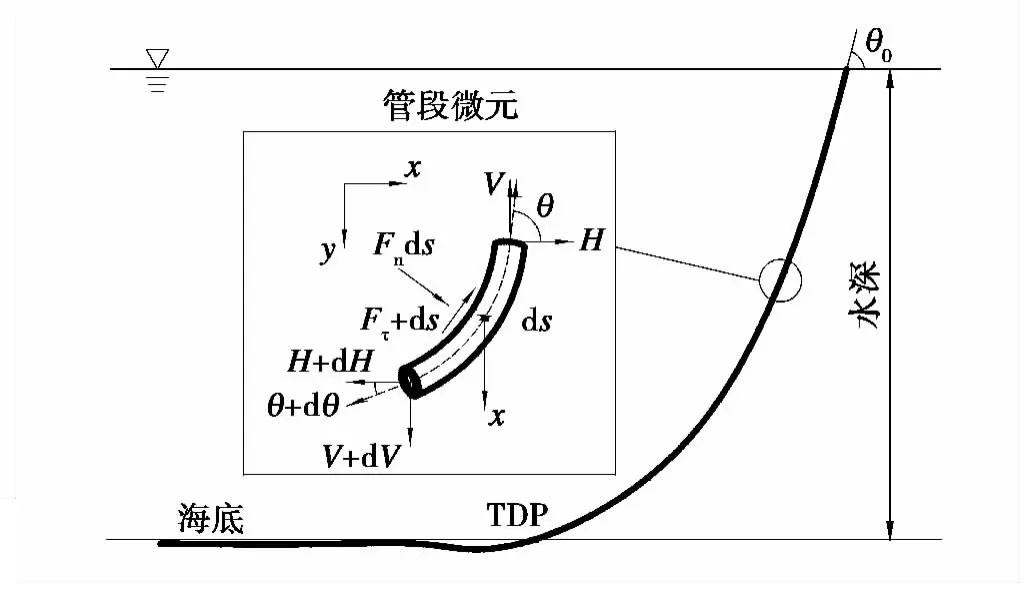
图5 悬浮段管段微元受力分析示意Fig.5 Force sketch of a differential element of suspended pipeline

可以得到θ角度以及管道在x、y轴的增量:

虽然在计算悬链线构型时忽略了管道的弯曲刚度,实际的管道弯矩可以用以下公式计算:


图6 触地段管段微元受力分析示意Fig.6 Force sketch of a differential element of pipeline laid on seabed
2.2 触地段
由于先前提到的许多文献主要讨论的都是刚性海底,在文中就不再讨论,主要讨论弹性海底刚度的情况。根据基础梁理论(见图6),管道在海底段的微分方程可表示为



式中:

当边界条件x→∞时,管道只受到自身重力和浮力的影响,式(8)中的c3,c4必须等于零,通解可简化为

管道触地段的弯矩可以用以下公式求得:

2.3 边界条件
对管道在铺管时所受的环境载荷情况进行分析,得到边界条件:

3 数值求解过程
在求解过程中管道顶部拉力TTOP是未知量,所以在该求解过程中得到正确的拉力值是主要目的之一。首先需要假设一个顶部拉力值,然后从管道顶端开始求解,将管道划分成n份微段,运用2.1节中的公式通过迭代法进行求解,直到触地点。根据边界条件,求解式(10)得到触地段的解析解,便可由悬浮段和触地段在触地点处弯矩连续的条件,|M1-M2|/M1<ε(其中ε是一个非常小的值)来判断TTOP的大小,最终通过二分法求解得到正确的顶部拉力、管道在铺管时的构型以及内力分布。具体求解过程如图7所示。
4 有限元模型
为了与理论计算结果作比较,使用通用有限元软件——ABAQUS分别对不同载荷和环境下的铺管安装过程进行分析[13],ABAQUS模型如图8所示。

图7 数值计算流程图Fig.7 Flow chart of numerical calculation

图8 ABAQUS模型示意Fig.8 Sketch of ABAQUS model
4.1 管道模型
柔性管采用梁单元(B31H),它能精确、高效地模拟细长管道。通过自定义梁单元的非线性拉力-应变、弯矩-曲率关系属性,能更精确地模拟出铺管时柔性管响应情况。
4.2 海底模型
采用3D解析刚性平面来模拟海底,并定义柔性管与海底之间的接触为线性接触,土壤刚度为2×105,同时忽略了管土之间的摩擦力。
4.3 边界条件
柔性管顶端受张紧器限制,在x、y、z方向上的位移以及绕x、z轴的旋转设置为完全固定。管道另一端置于海底并对其施加一个集中力。
5 结果分析
Bai Y已经研究了纤维增强热塑性塑料复合管在静态无流环境下,J-lay安装的有限元和理论方法并对结果加以分析与总结[12]。将在其基础上进一步讨论在不同水深、铺设角度和水流作用下,柔性管安装稳定性的有限元和理论分析的结果。
5.1 水深及铺设角度对铺管的影响
图9~12为管道的构型和弯矩曲率图。所在水深分别为100 m、150 m,铺设角度分别为78°、80°,流速分别为0.3、0.0、-0.3 m/s。管道的顶部拉力(TTOP)、在触地点处的管内轴向拉力(TTDP),以及铺设时管道承受的最大弯矩(MMAX)见表2。
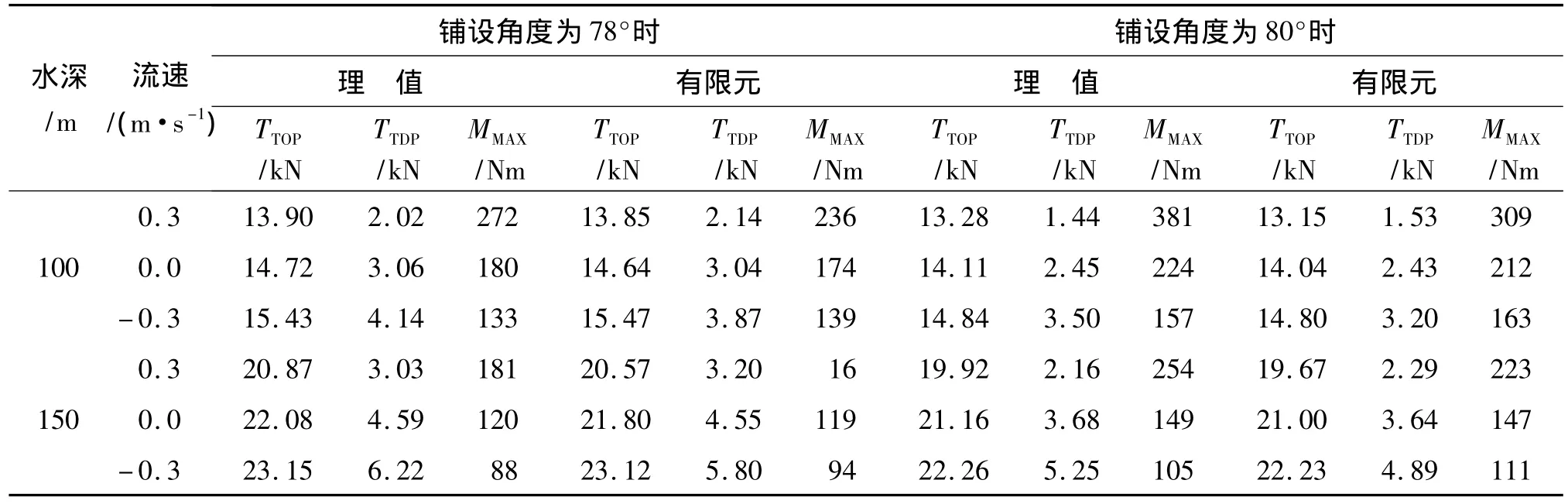
表2 两种水深下、铺设角度为78°和80°时,不同水流速度下的管道TTOP、TTDP和MMAXTab.2 TTOP,TTDPand MMAXfor 78°and 80°laid angles at 100 m and 150 m WD

图9 水深100 m铺设角度为78°时管道构型及弯矩对比Fig.9 Comparison of pipeline configurations and bending moments for 78°laid angle at 100 m WD
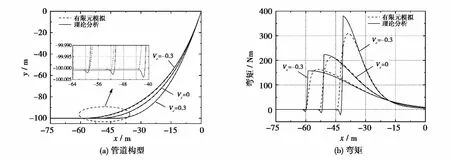
图10 水深100 m铺设角度为80°时管道构型及弯矩对比Fig.10 Comparison of pipeline configurations and bending moments for 80°laid angle at 100 m WD
该柔性管是由复合材料组成,弯曲刚度较小且具有非线性,因此文中采用自然悬链线法计算时,只能忽略管材的弯曲刚度;同时还采用非线性有限元法对其安装稳定性问题进行对比分析。从图9~12可以看出理论计算的结果和有限元模拟的结果比较接近,可以接受。但在触地点附近,管道弯曲变形明显,由于忽略了管材的弯曲刚度,所以理论结果相对于有限元结果偏于保守和安全的。当管道受到海流影响时会发生侧向偏移,而从弯矩图可以得到在触地点附近当有正向海流影响时,随着管道向正方向偏移,管道弯矩值增大;有负向海流影响时,管道则向负方向偏移,管道弯矩值减小。由表2可以看出,随着铺设角度增大,管道受到的弯矩也随之增大,但管道顶部的拉力却随之减小;随着铺设水深的增加,管道悬浮段质量增加,管道顶部拉力明显增加,但弯矩明显减小。

图11 水深150 m铺设角度为78°时管道构型及弯矩对比Fig.11 Comparison of pipeline configurations and bending moments for 78°laid angle at 150 m WD

图12 水深150 m铺设角度为80°时管道构型及弯矩对比Fig.12 Comparison of pipeline configurations and bending moments for 80°laid angle at 150 m WD
5.2 管道浮重的影响
图13、14所示为水深100 m,铺设角度为80°,在流速Vc=-0.3 m/s以及Vc=0.3 m/s时,分别取浮重116、224、358 N/m的管道构型和弯矩曲率的理论结果。管道的顶部拉力(TTOP)、在触地点处的管内轴向拉力(TTDP),以及铺设时管道承受的最大弯矩(MMAX)见表3。

表3 两种流速下不同浮重的管道的TTOP、TTDP和MMAXTab.3 TTOP,TTDPand MMAXfor different submerged weights with-0.3 m/s,0.3 m/s

图13 流速-0.3 m/s下不同浮重的管道构型及弯矩对比Fig.13 Comparison of pipeline configurations and bending moments for different submerged weights with Vc=-0.3 m/s
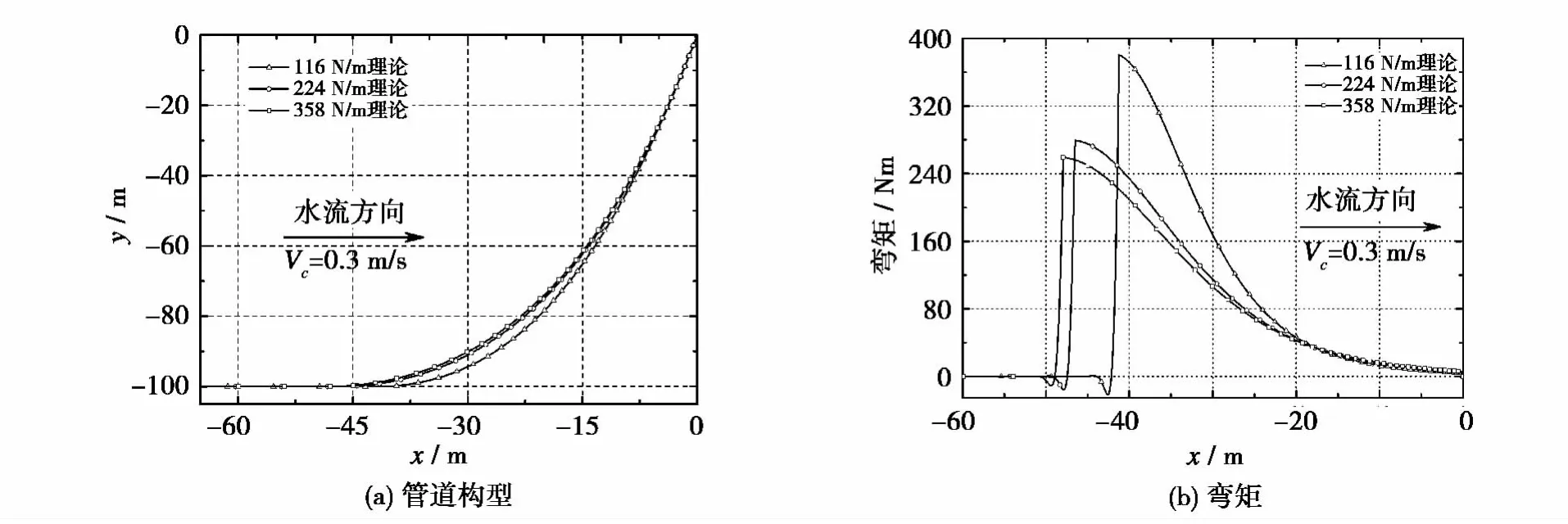
图14 流速0.3 m/s下不同浮重的管道构型及弯矩对比Fig.14 Comparison of pipeline configurations and bending moments for different submerged weights with Vc=0.3 m/s
浮重对于铺管分析而言是个非常重要的参数,由图13、14可以看出在水流作用下,浮重越大管道偏移则越小,管道的稳定性得到提高。当管道受到负向水流作用时,浮重小的管道虽然弯矩有所减小,但是随着流速的增大,管道偏离设计位置的距离越大,稳定性越差;当管道受到正向水流作用时,浮重小的管道不仅弯矩增大而且偏离设计位置的距离很大,对于管道铺设很不利。但如果只是增加管道的配重以增大浮重,会导致管道顶部拉力过大,在铺设过程中容易发生破坏,因此需要根据实际情况,选择合适的配重以满足稳性和铺设的要求。
6 结语
在之前的研究基础上,运用理论和有限元方法对柔性管的Reel-lay安装稳定性问题进行了对比分析。理论方法在计算速度、参数修改和软件编译上优于有限元法,可以对铺管进行初步分析,确定初始参数,速度快、效率高,减少有限元计算的工作量。由于该柔性管可以承受大于2.5 kNm的弯矩,而计算得到该管的顶部拉力和最大弯矩都没有超过该柔性管所能承受的极限强度和极限弯矩,因此可以判断管道没有发生破坏和整体屈曲。但是当水流流速不断增加,管道最终会由于偏离预设位置或者弯矩过大而导致破坏。为了保证柔性管Reel-lay铺设的安全性,以下几个因素需要考虑:
1)海洋环境:在铺设前需要对管道安装位置的海洋环境参数进行调研,需要选择有利的条件下进行铺管安装;
2)铺设角度:需要在可控制的范围内,通过调整铺设角度可以改变管道的构型,避免发生破坏;
3)顶部拉力:不能超过管道所能承受的极限拉力;
4)铺设深度:铺设深度不能超过该管道所能承受的最大铺设深度,这个与管道的所能承受的外压相关;
5)管道的浮重:增加浮重能改善管道铺设的稳定性,但是同时会增加顶部的拉力,并且对最大铺设水深产生影响;
6)卷筒半径:不得小于管道的最小弯曲半径。
因此,在设计柔性管Reel-lay铺设法时,并不能只考虑某个因素,需要结合实际情况,对多个因素加以综合考虑,才能保证柔性管铺设的稳定性和安全性。
[1] Bai Y,Bai Q.Subsea Engineering Handbook[M].2nd ed.USA:Gulf Professional Publishing,2010.
[2] Avery A,Martin S.Reinforced thermoplastic pipe-innovative technology for onshore field developments[C]//Proceedings of 22nd International Conference on Offshore Mechanics and Arctic Engineering.2003.
[3] Dixon D A,Rutledge D R.Stiffened catenary calculations in pipeline laying problem[J].Journal of Engineering for Industry,1968,90(1):153-160.
[4] Gong S,Chen K,Chen Y,et al.Configuration analysis of deepwater S-lay pipeline[J].China Ocean Engineering,2011,25(3):519-530.
[5] 龚顺风,何 勇,周 俊,等.深水海底管道S型铺设参数敏感性分析[J].海洋工程,2009,27(4):87-95.
[6] Gu Y N.Analysis of pipeline behabiours during laying operation[J].China Ocean Engineering,1989,3(4):477-486.
[7] Lenci S,Callegari M.Simple analytical models for the J-lay problem[J].Acta mechanica,2005,178(1):23-39.
[8] Wang L Z,Yuan F,Guo Z.Numerical analysis for pipeline installation by S-lay method[C]//OMAE-2010,29th International Conference on Ocean,Offshore and Arctic Engineering.2010.
[9] Wang L Z,Yuan F,Guo Z,et al.Numerical analysis of pipeline in J-lay problem[J].Journal of Zhejiang University,2010,11(11):908-920.
[10] Szczotka M.A modification of the rigid finite element method and its application to the J-lay problem[J].Acta Mechanica,2011,220(1):183-198.
[11] Bai Y,Wang Y,Cheng P.Analysis of reinforced thermoplastic pipe(RTP)under axial loads[C]//Proceedings of 3rd International Conference on Pipeline and Trenchless Technology,ICPTT 2012.2012.
[12] Bai Y,Yu B B,Cheng P.Offshore installation of reinforced thermoplastic pipe(RTP)[C]//ISOPE-2012,The International Society of Offshore and Polar Engineers,Rhodes(Rodos).2012.
[13]庄 茁,由小川,廖剑辉.基于 ABAQUS的有限元分析和应用[M].北京:清华大学出版社,2009.

