基于IIR数字滤波器的复合信号分离

张 莉，熊维德

（四川文理学院物理与工程技术系，四川达州 635000）

引言

随着信息时代和数字世界的到来，数字信号处理已成为极其重要的学科和技术，目前，它广泛应用于语音、图像、通信、控制、雷达、声纳、地震、生物医学、遥感遥测、地质勘探、航空航天、机械故障检测、自动化仪表等领域[1].数字滤波器是数字信号处理的重要内容，它可以用于抑制噪声，提取有用信号.具体分为有限长脉冲响应（IIR）和无限长脉冲响应（FIR）两种[2]，他们两者各有特色.IIR滤波器系统函数的极点可位于单位圆内的任何地方，因此零点和极点相结合，可用较低的阶数获得较高的选择性，所用的存储单元少，计算量小，经济高效.而FIR滤波器可以获得严格的线性相位，但其系统函数的极点固定在原点，在相同幅频特性指标下，FIR滤波器的阶数比较高，导致消耗的资源较多，成本增加.总体而言，在对相位没有严格要求的情况下，一般选择IIR滤波器更适用[3].

设计IIR数字滤波器一般采用间接法[4]（脉冲响应不变法和双线性变换法），其中，应用最广泛的是双线性变换法.其基本设计过程是：（1）先将给定的数字滤波器的指标转换成过渡模拟滤波器的指标；（2）设计过渡模拟滤波器；（3）将过渡模拟滤波器系统函数转换成数字滤波器的系统函数.常用的IIR模拟滤波器包括巴特沃兹、切比雪夫和椭圆滤波器等[5]，其中，巴特沃兹和切比雪夫滤波器阻带衰减是频率的单调减函数，而椭圆滤波器幅值响应在通带和阻带都是等波纹的，在相同的性能要求下，比巴特沃兹和切比雪夫滤波器所需的阶数低，且过渡带比较窄，可获得更为陡峭的衰减特性曲线.由于IIR滤波器的设计过程理论性很强，公式也复杂繁多，学生听起来比较抽象、枯燥，设计过程中只会简单地套用公式，不能深刻理解滤波器设计的本质，无法触类旁通.基于此，本文将Matlab引入实践教学，通过典型实例，介绍了数字滤波器在信号分离中的应用.既可增强学生的感性认识，有助于学生掌握滤波器设计的基本思想，又可锻炼学生的动手实践能力和创新意识.

1 基于IIR的复合信号分离

1.1 复合信号生成

设有一个由三路抑制载波调幅信号叠加构成的复合信号，其时域波形如下图1所示：

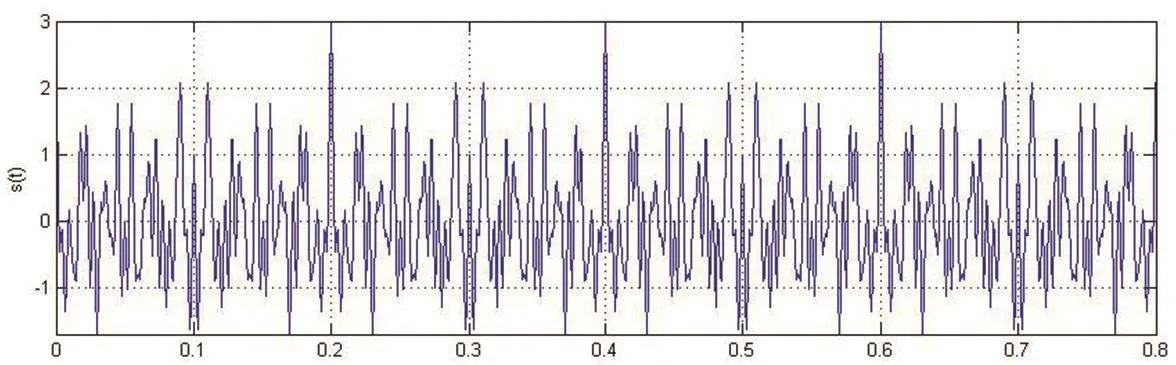
图1 复合信号s(t)的时域波形

抑制载波单频调幅信号的数学表达式定义为[6]：

1.2 频谱分析

由图1可见，三路信号混叠后的波形是无法在时域分离的.为了观察其频率特性，可对复合信号s(t)通过离散傅立叶变换求得信号的频谱，如下图2所示：

图2 s(t)的幅度频谱

由式（1）可知，抑制载波单频调幅信号实际就是两个正弦信号相乘，这两个信号的频率分别为和频和差频.所以，各路抑制载波调幅信号的频谱图是关于载波频率 对的两根谱线.由图2可见，这三路调幅信号的载波频率分别为50Hz、100 Hz和200 Hz.三路信号占有不同的频带且并不重叠，要分离出它们，只需分别通过低通、带通和高通滤波器进行滤波即可.

1.3 数字滤波器参数选择

数字滤波器阶数低，成本小，本文选用IIR滤波器进行仿真实验.要求滤波器的通带最大衰减Rp为0.05dB，阻带最小衰减Rs为80dB.为了使所设计的滤波器的阶数最低，我们选用椭圆滤波器，可调用Matlab工具箱中的ellipord和ellip函数实现.采样频率Fs取1000Hz，采样点数M取800.各类滤波器指标参数选取如下：

（1）对载波频率为50Hz调幅信号，可以用低通滤波器分离，其通带截止频率为，阻带截止频率为.实验结果如下图3-图5所示.

图3 低通滤波器的损耗函数曲线

图4 分离出的低频调幅信号的幅频特性曲线

图5 分离出的低频调幅信号的时域波形

由上图可知，其幅度特性可以满足设计要求，计算出滤波器的阶数为N1=8.

（2）对载波频率为100Hz调幅信号，可以用带通滤波器分离，其通带截止频率为，阻带截止频率为.实验结果如下图6-图8所示：

图6 带通滤波器的损耗函数曲线

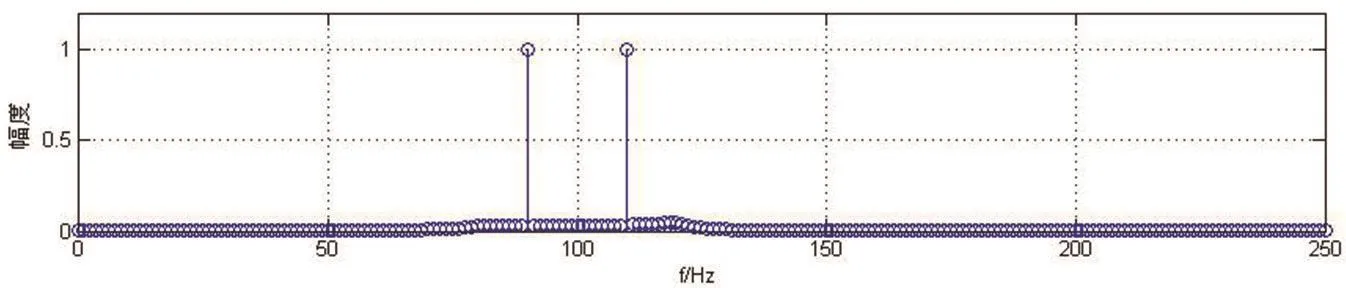
图7 分离出的中频调幅信号的幅频特性曲线

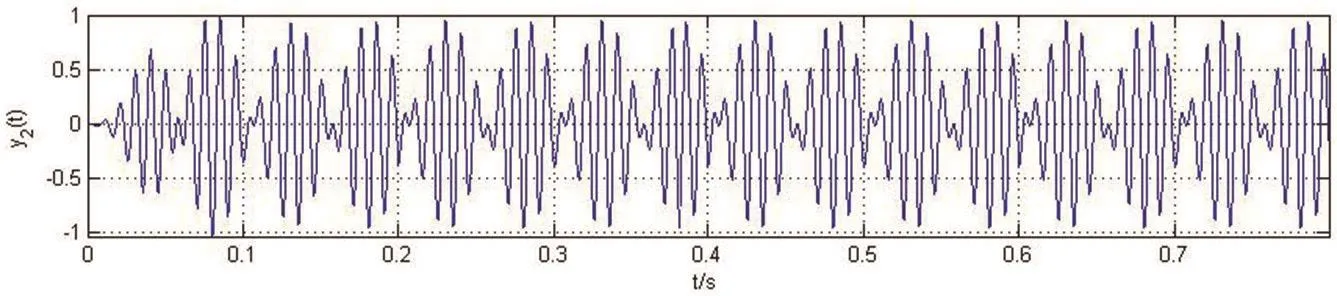
图8 分离出的中频调幅信号的时域波形

由上图可知，其幅度特性可以满足设计要求，计算出滤波器的阶数为N2=6.

（3）对载波频率为200Hz调幅信号，可以用高通滤波器分离，其通带截止频率为，阻带截止频率为.实验结果如下图9-图11所示：

图9 高通滤波器的损耗函数曲线

图10 分离出的高频调幅信号的幅频特性曲线

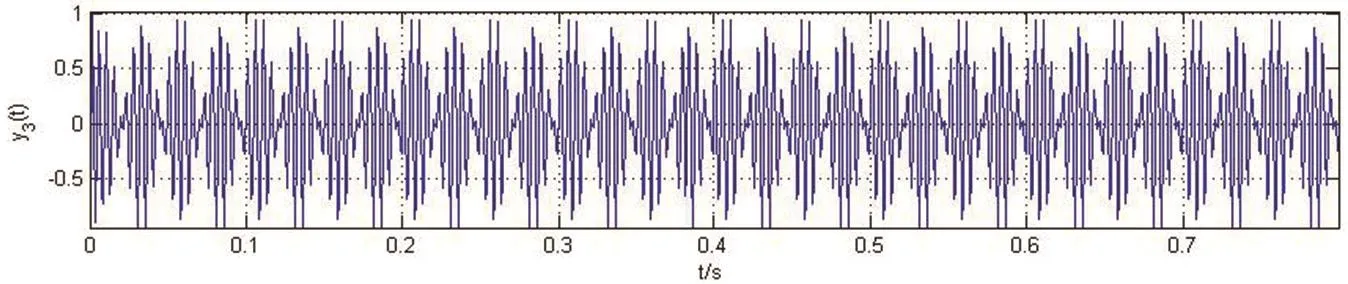
图11 分离出的高频调幅信号的时域波形

由上图可知，其幅度特性可以满足设计要求，计算出滤波器的阶数为N3=8.

由上述实验结果可知，通过所设计的三个数字滤波器已经准确地将时域上混叠的三路复合信号分离出来了.其中，时域波形可通过调用Matlab工具箱中的filter函数实现.

1.4 实验程序

1.4.1 复合信号生成函数：

1.4.2 时域离散系统损耗函数曲线绘图函数：

1.4.3 时域序列连续曲线绘图函数：

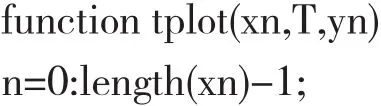
1.4.4 主程序：

2 结语

传统数字滤波器理论设计过程复杂、计算量大.本文以实例形式，介绍了IIR数字滤波器在信号分离中的应用，最后进行了Matlab仿真实验.实践表明，将Matlab引入教学，使学生从手工计算中解脱出来，将学习重点放在对数字滤波器设计方法的理解和运用上，既可激发学生的学习兴趣，又可锻炼学生的动手实践能力和创新意识，有利于提高教学效果.

[1][美]维纳.K.恩格尔,约翰.G.普罗克斯,刘树堂译.数字信号处理——使用Matlab[M].西安: 西安交通大学出版社,2002.

[2]余成波,陶红艳,杨菁等.数学信号处理及MATLAB实现(第二版)[M].北京:清华大学出版社,2008:74-78.

[3]吴镇杨.数字信号处理[M].北京:高等教育出版社,2005.

[4]万永革.数字信号处理的MATLAB实现[M].北京:科学出版社,2007.

[5]方勇.数字信号处理——原理与实践[M].北京:清华大学出版社,2005.

[6]高西全,丁玉美.数字信号处理[M].西安:西安电子科技大学出版社,2008.