一种文献推荐的因子图方法

许卓明，张 岩，林莉莉

(河海大学计算机与信息学院，江苏南京 210098)

文献推荐的目的是在一个文献库中向用户推荐满足用户兴趣的文献，以减少用户(尤其是领域初学者)搜索、浏览与筛选海量文献的巨大工作量。用户兴趣最普遍的表达方式是说明所需文献的主题。目前文献推荐主要有两类典型方法:内容过滤和协同过滤。内容过滤法是根据文献内容与用户兴趣的相似性来进行文献推荐，协同过滤法则是先找到与用户兴趣最相似的用户，然后根据最相似用户感兴趣的文献向当前用户推荐文献。

基于内容过滤的文献推荐代表性研究成果包括:Sugiyama等［1］假设某个研究者所发表的所有文献代表其研究兴趣，利用引文网络生成增强型的用户描述文件，并在实验中对初学者和资深研究者进行不同处理，获得了较高的推荐精度。由于传统基于内容过滤的推荐算法无法反映用户对文献的需求变化，曾春等［2］提出一种基于内容过滤的个性化推荐算法，利用领域分类模型上的概率分布来表达用户兴趣的模型，然后给出相似性计算和用户兴趣模型的更新算法。实验表明相对于传统矢量空间模型，这种概率模型能更好地表达用户的兴趣变化。

传统协同过滤算法的核心问题是计算用户兴趣相似度矩阵，但随着用户数目增长，这种矩阵计算将越来越困难，算法时空复杂度的增长和用户数的增长近似成平方关系。为缓解这个性能瓶颈，Sarwar等［3］提出了基于项的协同过滤算法，通过分析文献矩阵来确定不同文献之间的关系，并据此进行间接文献推荐。为避免传统协同过滤推荐中临近算法可能会引入噪音数据的问题，Naak等［4］在其研发的研究论文管理系统Papyres中提出了基于项的多准则协同过滤方法，允许用户在评价文献时针对文献的特定部分指定兴趣，增加了文献推荐的精度。

尽管以上传统文献推荐方法得到较广泛的应用，但仍存在以下不足:(a)基于内容过滤和协同过滤都需要在具有用户描述信息的情况下才能有效地推荐文献，但对于领域初学者，往往不存在用户描述信息;(b)未充分利用文献的主题概率分布和引文网络中文献间引用关系等重要信息，难以针对文献的主题向用户推荐与其兴趣主题相关的高质量文献。

针对现有方法的不足，笔者提出一种基于因子图［5］的文献推荐新方法。该方法将引文网络和文献的主题概率分布相结合，构造主题文献推荐的因子图模型;在该因子图模型上运用循环最大和(loopy maxsum)算法进行近似推理。该方法能发挥因子图简化概率图模型及其推理的优势，可在缺少用户描述信息的情况下向用户有效地推荐若干个主题下的高相关度文献。

1 基于因子图模型的文献推荐

1.1 文献主题概率分布计算

采用Tang等［6］提出的ACT(author-conference-topic)模型计算文献的主题概率分布。ACT模型中的conference可泛指文献发表刊物，包括会议论文集或期刊［6］。ACT模型是一个能综合建模文献、作者、发表刊物的主题概率模型，它利用主题分布来表示作者、文献和发表刊物之间的相互依赖关系;通过吉布斯采样(Gibbs sampling)进行参数估计，并计算给定作者的主题概率分布、给定主题的词概率分布以及给定主题的发表刊物概率分布。

根据ACT模型的特点，笔者将引文网络(包含文献标题、摘要、作者和发表刊物等信息)和主题数目(例如30)作为ACT模型的输入，在因子图建模时自动生成给定数目的主题并计算引文网络中每篇文献的主题概率分布p(divi)。

1.2 文献推荐的因子图模型

文献推荐的目标是针对输入的引文网络(含计算好的文献主题概率分布)，推理产生各主题下按主题相关度从大到小排序的前k个文献(本文设k=50)，以便用户从中选取文献，此问题可作如下描述。

输入:引文网络 G(V，E，C，D)，其中，V={vi}(i=1，2，…，n)代表文献 vi的集合，n 为引文网络中文献总数;E={eij}(j=1，2，…，n)代表引文网络的边集合，eij代表文献vi引用文献vj;C={ci}为文献被引频次的集合，ci为文献 vi被引文网络中其他文献引用的频次;D={di}为文献主题概率分布的集合，di=(α1，i，α2，i，…，αm，i)为文献vi在全部m个主题下的主题概率分布，m为引文网络中主题数(根据引文网络覆盖的领域主题宽窄来设定，例如可设 m=30)，主题变量 z=1，2，…，m，αz，i表示文献 vi属于主题 z的概率，显然

处理:针对输入建立文献推荐因子图模型，并在该因子图模型上进行近似推理(approximate inference)。

输出:m个主题下按主题相关度从大到小排序的相关文献列表，从中获取前k个文献(k=50)。

因子图是一个二部图，用来描述某个变量集上的一个全局函数如何因式分解为若干变量子集上的局部函数的乘积［5］:

式中:J——离散索引集;Xj——{x1，x2，…，xn}的子集，即 Xj⊆{x1，x2，…，xn};fj(Xj)——以 Xj中元素为自变量的局部函数。

因子图有两类节点:每个变量xi对应一个变量节点(用小圆圈表示)，每个fj(Xj)对应一个因子节点(用小方块表示)。当且仅当xi是函数fj(Xj)的自变量时，相应变量节点与相应因子节点之间才有一条无向边相连。

笔者构建的因子图模型包含观察变量集合{vi}、隐含变量集合{yz，i}以及特征函数(包括节点函数gz，i(yz，i)和边特征函数 fz，ij(yz，i，yz，j))，其中 yz，i∈{0，1}，是观察变量 vi在主题 z下对应的隐含变量，yz，i=0 表示文献vi与主题z不相关，yz，i=1表示文献vi与主题z相关。

图1是包含4个变量节点的文献推荐因子图模型。在该模型中，节点特征函数gz，i(yz，i)代表文献自身特点对该文献成为被推荐文献的影响程度。由于每篇文献属于某个主题z的概率不同，概率较大的更易于成为主题z下的被推荐文献。当概率大于给定阈值时，被引频次越大的文献就越有可能成为主题z下的被推荐文献;反之，当概率小于给定阈值时，被引频次越大的文献就越有可能成为其他主题下的被推荐文献。基于以上思想，可定义gz，i(yz，i)为

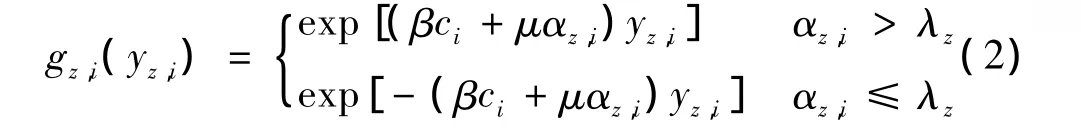
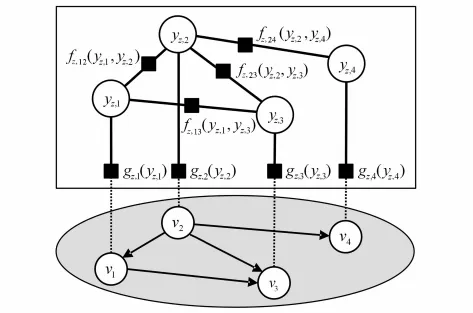
图1 文献推荐因子图模型Fig.1 Factor graph model for literature recommendation

其中

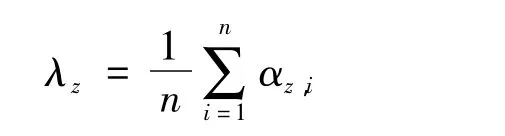
式中:β，μ——权重系数，β，μ∈［0，1］，β + μ =1;λz——文献的主题概率阈值。

可依据ci(用β表示)和αz，i(用μ表示)的相对重要程度进行调整。例如，当 ci占80%权重，αz，i占20%权重，则 β=0.8，μ =0.2。

fz，ij(yz，i，yz，j)代表文献之间引用关系对文献成为被推荐文献的影响程度。由于di可看作向量，因此采用余弦相似度来度量文献之间的主题相似度，相似度值越大，表明文献之间的主题相似度越高，反之亦然。基于以上思想，可定义 fz，ij(yz，i，yz，j)为

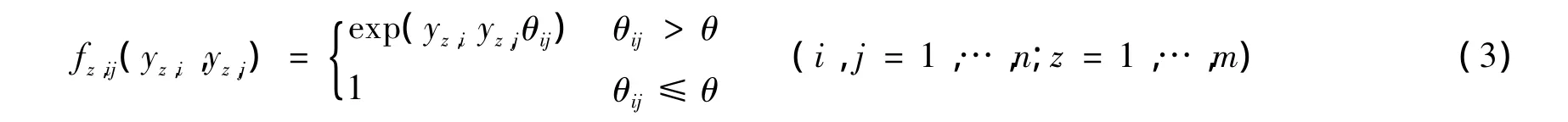
其中

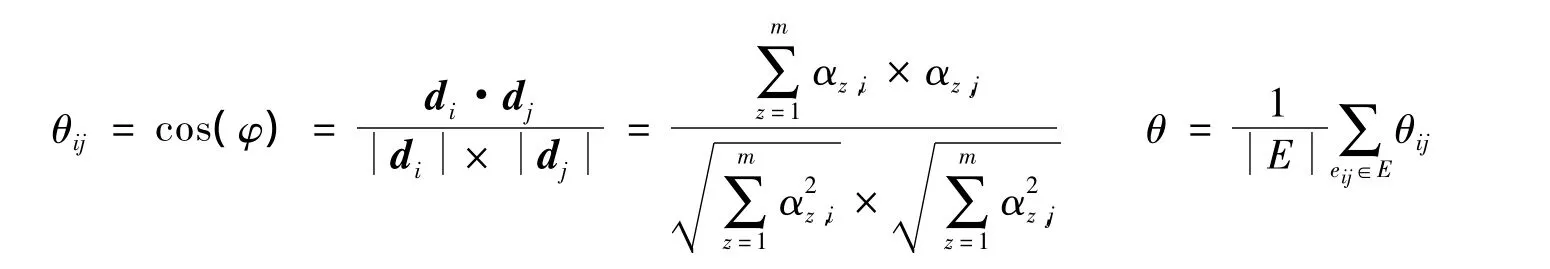
式中:θij——文献vi与 vj的主题相似度;φ——向量 di与 dj间的夹角。

为了简化模型，可假设主题之间是相互独立的［7］。基于特征函数以及概率建模的特点，考虑到因子图与概率图模型的对应关系［8］，可认为因子图模型对应的概率图模型是一个马尔可夫网络。根据概率论中马尔科夫网络的因式分解特性原理［8］，概率图中所有节点的联合概率分布 p(yz，1，yz，2…，yz，n)是图中所有最大团上势函数的乘积;而局部最大团上的势函数可定义为该团所包含的全部节点特征函数与边特征函数的乘积，因此可得出主题z下的联合概率分布为

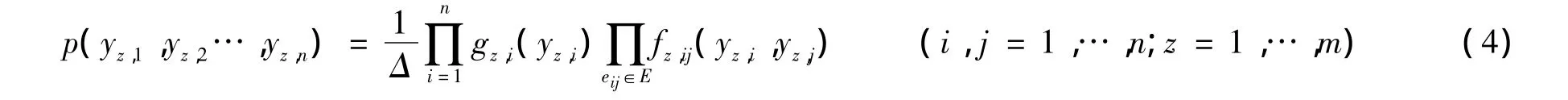
其中

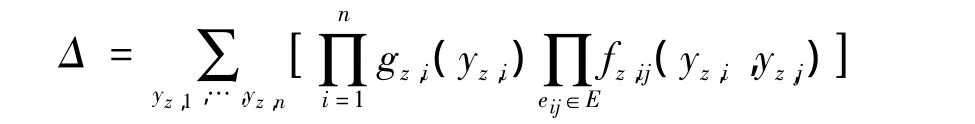
式中:Δ——归一化常数，亦称配分函数;1/Δ——在变量空集上的一个因子，为常数。

基于因子图的推理问题属于动态规划问题，即针对式(4)定义的目标函数p(yz，1，yz，2…，yz，n)找到一个隐含变量配置空间(yz，1，yz，2…，yz，n)，使得联合概率值达到最大。

1.3 基于因子图的文献推荐推理

因子图模型是一个有环因子图，由于传统的和-积算法［5］不能有效解决有环因子图的推理问题，因此笔者选用循环最大和算法［8］。为保证推理算法收敛，选用串行消息调度机制［8］，并给定循环最大和算法推理算法中两类消息函数为

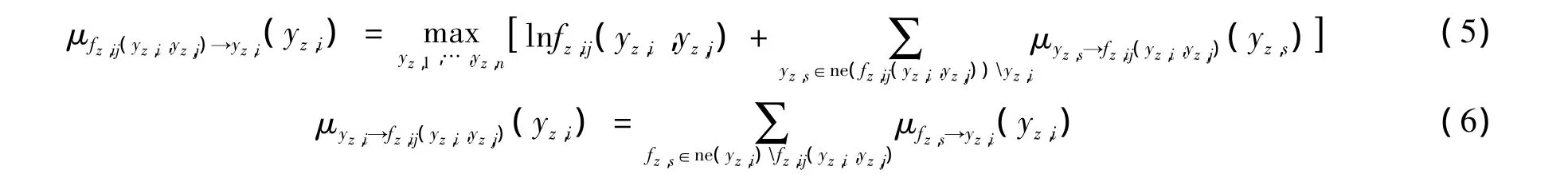
式中:ne(fz，ij(yz，i，yz，j))yz，i——与 fz，ij(yz，i，yz，j)相邻的除 yz，i外的其余变量节点的集合;ne(yz，i)fz，ij(yz，i，yz，j)——与 yz，i相邻的除 fz，ij(yz，i，yz，j)外的其余因子节点的集合。

当 yz，i和 fz，ij(yz，i，yz，j)作为叶子节点时，需要初始化消息:μyz，i→fz，ij(yz，i，yz，j)(yz，i)=0，μfz，ij(yz，i，yz，j)→yz，i(yz，i)=ln fz，ij(yz，i，yz，j)。当算法收敛时，可得节点 yz，i的边缘概率为

推理任务包括:利用式(5)、式(6)进行迭代计算，使式(4)定义的联合概率值达到最大，得到此时的隐含变量配置空间(yz，1，yz，2，…，yz，n)以及式(7)定义的每个隐含变量的边缘概率 p(yz，i)。根据节点特征函数定义(式(2))，在某个主题z下，文献的边缘概率值越大，表明该文献与主题z越相关。完成推理计算后，根据联合概率值最大时的(yz，1，yz，2，…，yz，n)选取所有满足 yz，i=1 (i∈{1，2，…，n})的文献 vi构成与主题 z相关的文献列表，对该列表中文献按其边缘概率值降序排序，从中选择前k个文献(k=50)构成主题z下的被推荐文献。

2 实 验

2.1 实验数据

实验数据集由笔者访学和合作研究的机构——美国印第安纳大学图书馆与信息科学学院提供。数据集是该学院学者已发表文献［9］中实验数据集的一部分，来自于Thomson Reuters公司出版的2008年版期刊引证报告(Journal Citation Reports，JCR)。笔者从该JCR报告中选取“信息科学和图书馆学”类属中共计59个SCI期刊从2006年1月到2010年3月的全部引文数据构成一个引文网络，其中包含10 508篇文献和20221个文献引用关系。

2.2 因子图方法的实现

2.2.1 主题概率分布计算

采用清华大学提供的ACT原型建模工具［6］进行实验。根据文献计量学领域的研究经验，一般将文献库(即引文网络)划分为30～50个主题，本文指定主题数目为30(即m=30，主题编号为1～30)。对实验数据集文件进行预处理，转换为满足ACT模型输入格式要求的文献库文件。将预处理后的文献库连同主题数目(30)一起输入到ACT原型建模工具中，从该原型建模工具的输出结果中选取需要的计算结果，即文献库中给定数目的主题(其编号为1，2，…，30)以及每篇文献在这些主题上的概率分布。例如，表1为其中8个主题及其条件概率值排序前10的词。

表1 8个主题及其条件概率值排序前10的词Table 1 Eight topics and their top-ten words ordered by conditional probability value

2.2.2 因子图建模及文献推荐推理

a.因子图建模的实现。按经验选取β=0.8，μ=0.2;β=μ=0.5;β=0.2，μ=0.8共3组不同参数值。通过Java编程读入引文网络，根据文献间的引用关系计算引文网络中每篇文献的被引频次。基于已计算获得的文献主题概率分布，每组参数值下的因子图文件生成过程如下:(a)利用式(2)计算节点特征函数值;(b)利用式(3)的θij计算文献间的主题相似度，并计算阈值θ，再由阈值θ和文献间的主题相似度用式(3)计算边特征函数值;(c)利用计算得到的节点特征函数值和边特征函数值，建立满足循环最大和推理算法要求的因子图文件。

b.基于因子图的文献推荐推理的实现。选用libDAI软件包［10-11］中已实现的循环最大和推理算法来完成推理任务。libDAI软件包是一个免费的开源C++库，能实现由离散值变量构成的各种概率图模型——包括有向图模型(贝叶斯网络)、无向图模型(马尔可夫网络、因子图)的多种精确和近似推理算法。将已建立的因子图文件作为输入，在Ubuntu系统下运行libDAI软件包中的循环最大和算法。为了保证算法收敛，设定算法最大迭代次数为10 000次，选择串行消息调度机制。在该算法的每次迭代中，不断更新式(5)(6)两类消息。当算法收敛时，获得的推理结果包括式(4)定义的联合概率最大值、隐含变量配置空间、式(7)定义的隐含变量的边缘概率值。

2.3 对比方法及评价基准

2.3.1 对比方法

为比较本文所提因子图算法与传统算法的优劣，选择了2个对比方法。由于协同过滤方法在没有用户历史描述信息的情况下无法进行文献推荐，因此本文选择了没有利用引文网络中文献间引用关系和文献主题概率分布的基于内容过滤方法，以及仅利用引文网络中文献主题概率分布的朴素方法作为2个对比方法。

a.基于内容过滤方法。方法思想:通过计算引文网络中每篇文献与用户兴趣主题的相似性，向用户推荐相似性较高的文献。

方法实现:由于缺少用户兴趣主题，假设每个主题下条件概率值排名前10的词代表用户的兴趣主题。通过ACT模型输入引文网络和主题数目，计算给定每个主题下的词的条件概率分布p(dw)(dw为词的主题概率分布)，对每个主题下的词按照该条件概率值进行降序排序，得到排序前10的词集合(见表1)。利用Java编程计算引文网络中每个主题条件概率值排名前10的词在每篇文献上的TF-IDF值，按照TF-IDF值对文献进行降序排名，选取前k(k=50)个文献组成文献推荐列表。

b.朴素方法。方法思想:基于主题概率分布和文献被引频次进行文献推荐，在文献主题概率值大于给定阈值λz的情况下，按照文献被引频次从高到低向用户推荐文献。

方法实现:依据上述ACT模型生成的文献主题概率分布，利用Java编程将主题概率值大于λz的文献加入候选文献列表，再按照文献被引频次对候选文献列表进行降序排名，选取前k(k=50)个文献组成文献推荐列表。

2.3.2 有效性评价基准

选择归一化折扣增益值(normalized discounted cumulative gain，nDCG)［12］作为方法有效性评价基准。nDCG值是信息检索领域中衡量搜索算法或相关应用有效性的常用度量。由于基于主题的文献推荐可以看作是一种给定主题的文献检索，因此nDCG值可作为评价基准来衡量文献推荐方法获得主题高相关性文献的能力(nDCG值越高表明方法的有效性越高)。

在计算nDCG值之前必须首先计算折扣增益值(discounted cumulative gain，DCG)。通过对排在文献推荐列表前k个文献的分级相关度累计加权计算，可得到DCG值。用τ表示DCG值，τk的计算公式［12］为

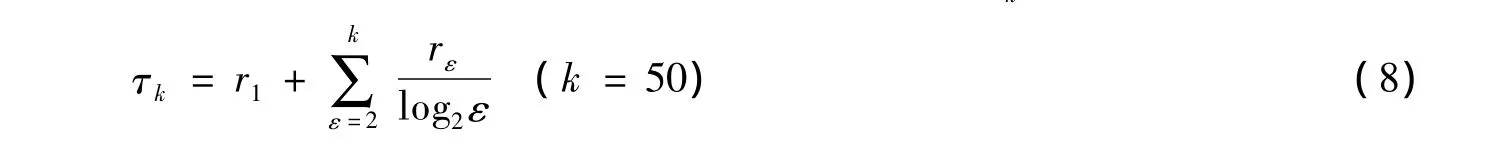
式中rε(ε=1，…，k)为排在文献推荐列表中第ε位的文献的分级相关度。

完成DCG值计算后，还需计算理想折扣增益值(ideal discounted cumulative gain，IDCG)。IDCG值是指对文献推荐列表中k个文献按照它们的分级相关度rε(ε=1，…，k)降序排列后，重新计算得到的DCG值。用η表示nDCG值，用ω表示IDCG值，得到ηk计算公式［12］为

采用Java编程实现nDCG值的计算。通过ACT模型设定λz，获得每个主题的综述文献，文献的分级相关性定义为其被综述文献引用的频次。

2.4 实验结果与讨论

图2是因子图方法与基于内容过滤方法及朴素方法在30个主题下分别推荐前50篇文献所得到nDCG值的比较。如图2(a)所示，在因子图方法中，当参数取值为β=0.8，μ=0.2时，得到的nDCG值优于另外2组参数的nDCG值，表明此参数值下因子图方法的文献推荐效果最佳。由于β代表文献被引频次所占权重，μ代表文献主题概率所占权重，因此实验结果进一步说明因子图方法中文献被引频次对文献成为被推荐文献的影响比文献主题概率分布的影响要大。如图2(b)所示，与朴素方法相比，因子图方法(β=0.8，μ=0.2)在30个主题上的nDCG值均大于朴素方法;由于朴素方法没有使用引文网络，进一步表明引文网络的引入可以提高文献推荐效果。与基于内容过滤方法相比，因子图方法在其中29个主题上完全优于基于内容过滤方法，说明因子图方法综合考虑了文献本身特点以及引文网络，对推荐效果有很大提升;其中一个主题(编号为17)下的推荐效果差于基于内容过滤的方法，说明文献内容因素对文献成为被推荐文献也有一定影响。

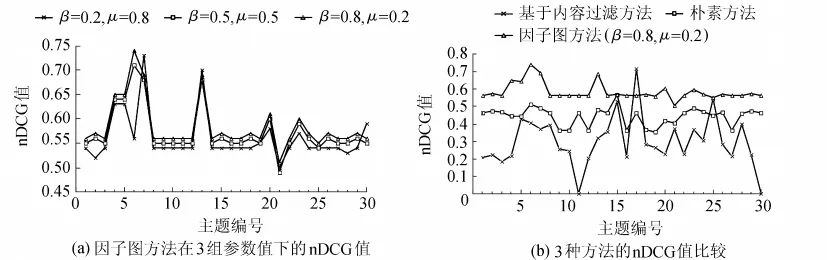
图2 nDCG值计算结果比较Fig.2 Comparison of calculated nDCG values

实验结果表明，在缺少用户描述信息时，因子图方法总体上明显优于传统的基于内容过滤方法和朴素方法。

3 结 语

为了克服传统文献推荐方法在缺少用户描述信息(如用户历史兴趣或当前兴趣主题)时无法有效地向用户推荐文献的缺陷，笔者提出一种基于因子图模型的文献推荐新方法。该方法通过将引文网络信息(包括文献发表信息、文献引用关系及被引频次等)及文献本身特点(文献的主题概率分布)进行统一建模，实现利用主题概率模型自动生成引文网络中给定数目的主题，并计算出各主题下按主题相关度从大到小排序的若干个相关文献，供用户选择。该方法还能充分发挥因子图简化概率图模型及推理的优势，提高主题文献推荐的效果。基于权威引文网络(Thomson Reuters公司出版的2008年版期刊引证报告)的实验结果表明，在缺少用户描述信息的情况下，因子图方法的推荐效果明显优于基于内容过滤方法和朴素方法等传统方法，从而为文献推荐研究提供了新思路。因子图方法涉及多个参数(β，μ)，为了简化实验，笔者根据经验选择了几组不同的参数值进行实验，下一步可考虑通过参数学习的方法来训练出具有最佳文献推荐效果的最优参数值组合。

致谢:感谢美国印第安纳大学图书馆与信息科学学院博士研究生Yan Erija为本文研究提供了实验数据集;感谢清华大学计算机科学与技术系唐杰副教授为本文实验提供了ACT原型建模工具。

［1］SUGIYAMA K，KAN M Y.Scholarly paper recommendation via user's recent research interests［C］//HUNTER J，CARL L，GILESCL，et al.Proceedings of the 10th annual joint conference on digital libraries.New York:ACM，2010:29-38.

［2］曾春，邢春晓，周立柱.基于内容过滤的个性化搜索算法［J］.软件学报，2003，14(5):999-1004.(ZENG Chun，XING Chunxiao，ZHOU Lizhu.Personalized search algorithm using content-based filtering［J］.Journal of Software，2003，14(5):999-1004.(in Chinese))

［3］SARWAR B M，KARYPISG，KONSTAN J A，et al.Item-based collaborative filtering recommendation algorithms［C］//SHENV Y，SAITO N，LYU M R，et al.Proceedings of the 10th international world wide web conference.New York:ACM，2001:285-295.

［4］NAAK A，HAGE H，AÏMEUR E.A multi-criteria collaborative filtering approach for research paper recommendation in Papyres［C］//BABIN G，KROPF P，WEISS M.Proceedings of the 4th International MCETECH Conference on E-technologies，as Lecture Notes in Business Information Processing(LNBIP)vol.26.Heidelberg:Springer Berlin Heidelberg，2009:25-39.

［5］KSCHISCHANG F R，FREY B J，LOELIGER H-A.Factor graphs and the sum-product algorithm［J］.IEEE Transactions on Information Theory，2001，47(2):498-519.

［6］TANG Jie，JIN Ruoming，ZHANG Jing.A topic modeling approach and its integration into the random walk framework for academic search［C］//GIANNOTTI F，GUNOPULOSD，TURINI F，et al.Proceedings of the 2008 Eighth IEEE International Conference on Data Mining.Los Alamitos:IEEE Computer Society，2008:1055-1060.

［7］TANG Jie，SUN Jimeng，WANG Chi，et al.Social influence analysis in large-scale networks［C］//ELDER J，FOGELMAN F S，FLACH P，et al.Proceedings of the 15th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.New York:ACM，2009:807-816.

［8］BISHOPC M.Pattern recognition and machine learning［M］.Berlin:Springer，2006:359-422.

［9］YAN Erjia，DING Ying.Library and information science(LIS)as we see it:an overview at the state and country level from 1965-2010［C］//Proceedings of the American Society for Information Science and Technology.Malden MA，USA:Wiley Subscription Services，Inc，2011:1-8.

［10］MOOIJJM.libDAI:A free and open source C++library for discrete approximate inference in graphical models［J］.Journal of Machine Learning Research，2010，11:2169-2173.

［11］MOOIJ JM.libDAI-A free and open source C++library for discrete approximate inference in graphical models［EB/OL］.［2013-01-14］.http://cs.ru.nl/～jorism/libDAI/.

［12］JÄRVELIN K，KEKÄLÄINEN J.Cumulated gain-based evaluation of IR techniques［J］.ACM Transactions on Information Systems，2002，20(4):422-446.