膜材厚度偏差对充气天线反射面精度的影响

何小斐，伞冰冰，朱召泉

(河海大学土木与交通学院，江苏南京 210098)

近年来，随着移动卫星通信、对地观测等的迅猛发展，对大型空间可展天线的需求越来越迫切。充气天线是以柔性薄膜材料制成的一种高精度空间结构，具有质量轻、折叠体积小、成本低等优点［1］，是未来大型航天结构的理想选择。太空充气天线(图1)一般由反射器、支撑圆环、支撑管等组件构成，其中反射器由上下两片对称的抛物面(反射面)薄膜组成，呈凸透镜状。信号穿过下片透波罩，在上片镀金属的反射面上反射而收集在馈源处。反射面的成形精度即实际曲面形状与设计曲面的接近程度，直接影响收发信号能力的强弱。因此，充气天线结构对膜面的成形精度要求极高，成形精度是充气天线设计和成形中的一个重要指标。

图1 充气天线Fig.1 Inflatable parabolic antenna

近年来，各国学者以提高反射面几何精度为主要目标，对充气天线的设计方法进行了大量研究。主要思路有:(a)将设计抛物面作为初始曲面，将其充气后获得天线的实际几何曲面。Naboulsi［2］分析了内压和边界条件对反射面成形精度的影响。Greschik等［3-4］考虑均匀分布和线性非均匀分布两种膜材厚度偏差分布形式下不同焦径比和气压对反射面成形精度的影响，得出成形精度随焦径比和气压增大而减小的结论。徐彦等［5-6］对某一形状的充气天线系统进行设计，分析了该系统下膜材厚度的设计值、内压等对反射面成形精度的影响，并提出调整方法。该思路对充气天线的精度研究有一定指导作用，但是以设计曲面为基准进行充气而获得的曲面与设计曲面存在差异。(b)寻找设计曲面对应的零应力曲面，即未充气曲面，并将其作为分析的初始曲面。伞冰冰［7］将非线性有限元逆迭代法引入充气天线的设计中，通过逆迭代可以获得目标曲面对应的零应力曲面，对其进行充气，理论上可以获得精确的目标设计形态。毛丽娜等［8］以非线性有限元逆迭代法为基础，运用无矩理论建立反射面结构分析模型，通过对具体算例的分析，发现反射面成形精度随口径和焦距的增大而降低。

无论设计方法如何完善，在充气天线的实际成形过程中不可避免地会存在一些影响因素，如边界点位置误差、膜材实际厚度与设计值之间的偏差、气压误差、裁剪下料误差等，都会对反射面成形精度造成影响，使实际曲面形状与设计值产生差异。而关于这些因素是如何影响反射面成形精度的、影响程度如何等研究相对较少，因此难以给出有效的误差控制措施。

本文以非线性有限元逆迭代法为基础，针对膜材厚度偏差对充气天线反射面成形精度的影响进行研究，分析均匀分布及线性非均匀分布两种典型的膜材厚度偏差分布形式对充气天线反射面的影响规律和影响敏感度，并进一步考虑了不同反射面焦径比的影响。

1 设计方法和分析方案

1.1 设计方法

非线性有限元逆迭代法早前应用于张弦梁结构和索网结构的找形分析，是由已知的初始状态逆迭代求出结构零应力几何形状的过程［9-10］。本文将非线性有限元逆迭代法应用于充气天线反射面(抛物面)的设计中:首先利用非线性有限元逆迭代法对设计抛物面进行应力释放，得到设计抛物面充气前的初始零应力状态;然后再对该零应力状态进行充气成形。逆迭代具体步骤如下(图2，图中d n表示经n次迭代调整后所得形态与目标形态的差异):(a)假定一个初始零应力状态，赋予真实弹性模量，对其加压得到平衡后的形态;(b)比较(a)所得形态与目标形态(即设计抛物面)的差异，并据此调整假定的零应力状态，再重复(a);(c)直至(a)调整所得形态与目标形态吻合程度满足精度要求，调整结束，此时所获得的零应力状态即为目标形态对应的零应力状态。

图2 逆迭代法应力释放示意图Fig.2 Sketch map of stress releasing based on inverse iteration method

非线性有限元逆迭代法可避免膜单元应力释放时出现大量松弛的现象，且可以通过反复迭代提高计算精度，得到较为精确的零应力曲面，再对其进行充气得到的成形几何曲面较为精确。

1.2 形面误差的分析方法

1.2.1 形面误差概念

评价充气天线反射面的成形精度不能仅由面上个别点来判断，通常是根据反射面设计值与实际值的均方根误差 δRMS［11］来评价:

式中:Δdi——实际成形模拟曲面上的点i与设计曲面上对应点之间的距离残差;m——结点数目。

另外，为了解成形模拟后曲面上任意点的高度较设计值的变化趋势，对成形曲面与设计曲面上对应点之间的垂直距离差d zi进行分析。d zi＞0代表考虑误差后，曲面上点i比设计值高，即成形曲面偏高;d zi＜0则相反。

1.2.2 敏感性分析方法［12］

建立误差系统模型:

其中

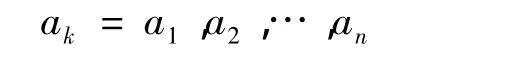
式中:E——形面误差，本文用δRMS描述;ak——误差影响因素，本文指膜材厚度偏差。

在分析ak对E的影响时，将其余影响成形精度的因素取为设计值，即可得到

由式(3)可了解E对ak扰动的敏感程度。

采用无量纲化的敏感度函数Sk对敏感程度进行描述，即将误差的相对值δE=/E与ak相对误差δak=/ak的比值定义为E对ak的敏感度函数Sk:

Sk值越大，表明E对ak越敏感。通过对Sk的比较可以对不同膜材厚度偏差的敏感性进行量化的对比评价。

1.3 分析方案

1.3.1 抛物面参数和有限元模型

本文研究的反射面为抛物面，方程表示为

式中F为抛物面焦距。

抛物面口径D为3000 mm，保持口径不变，取焦径比F/D=0.25，0.50，0.75，1.00，1.25，1.50。其他材料参数为:膜材弹性模量 E=2.5 ×109Pa，泊松比μ=0.34，膜材厚度设计值t=2.5×10-3mm，设计气压p=10 Pa。

根据结构的对称性，取反射面的1/4进行分析，有限元模型如图3所示。两条径向边界施加对称约束条件，周边固支。

1.3.2 膜材厚度偏差分布类型

实际膜材的厚度偏差分布具有多种可能的形式。本文在线性分布形式［4］的基础上，针对均匀分布形式及线性非均匀分布形式探讨膜材厚度偏差对成形精度的影响。

图3 抛物面有限元模型Fig.3 Finite element model of paraboloid membrane structure

均匀分布即是指整个反射面的厚度偏差Δt为均值(中心点处膜材厚度变化的百分数，Δt为正值代表厚度增大，负值代表厚度减小)。分析时取Δt=0，±5%，±10%，±15%，±20%进行研究。

线性非均匀分布是指偏差值沿着抛物面径向线性变化，本文选择a类和b类两种线性变化方式进行分析(图4)。a类为中心点处厚度偏大，边界处厚度偏小;b类为中心点处厚度偏小，边界处厚度偏大。取=0，5%，10%，15%，20%的a类和b类情况进行研究。面上各点厚度的计算公式为

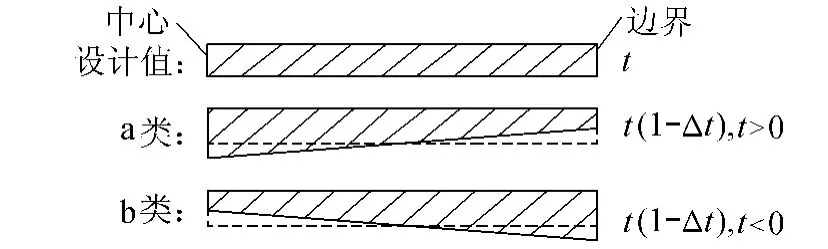
图4 膜材厚度线性偏差形式Fig.4 Linear deviation of membrane thickness

式中:ti——抛物面上各点膜材厚度，mm;R——抛物面半径，mm;ri——抛物面上各点距离结构中心点的水平距离，mm。

2 膜材厚度偏差均匀分布对抛物面形面精度的影响

2.1 一般规律

以焦径比F/D为1.50的充气天线抛物面为例，对膜材厚度偏差均匀分布情况进行误差分析。Δt=±10%，±20%时的形面误差分布见图5。由图5可以看出:

a.比较膜材厚度偏大和偏小的两类情况，厚度偏小时，整个膜面上的点都较设计曲面偏高;厚度偏大时，除了边界附近部分曲面上的点偏高外，大部分曲面都较设计曲面偏低。

b.比较厚度偏大(或偏小)不同绝对值的情况发现，形面误差随着厚度偏差绝对值的增大而增大。

c.在相同的膜材厚度偏差下，越靠近边界的点，由于受到边界固定约束的影响较大，变形受到限制，其形状偏差越小。

图6为旋转母线L1(图5(b))上各点的垂直距离差d zi，图中横坐标为母线上各点距中心点的水平距离r与R的比值r/R。为了了解在每种膜材厚度偏差下d zi的变异程度，采用变异系数Cv来描述［13］。Cv是衡量某组数据变异程度的统计量，表示为

式中μ和σ分别为数据的平均值和标准差。

将L1均分为10个区段(区段1:r/R=0.0～0.1;区段2:r/R=0.1～0.2;……)，分别计算每个区段内d zi的Cv(图7)。经分析发现，当r/R=0.2～0.6时，d zi的变异系数接近于0，离散程度较低。此结论可以应用于充气反射面天线的设计中:选取d zi离散程度较低的区段(r/R=0.2～0.6)作为反射面有效区域，这样有利于采用统一措施补偿膜材厚度偏差均匀分布带来的误差。

进一步计算抛物面在上述各种偏差下的δRMS(图8)及δRMS对膜材厚度偏差的敏感度(图9)。由图8可以看出，形面δRMS随Δt绝对值的增大而增大;膜材厚度偏小比偏大时产生的δRMS大。由图9可以看出，膜材厚度均匀分布偏小时δRMS对Δt的敏感度更大，说明膜材厚度偏小对于抛物面的成形精度影响更大。这是由于膜材厚度偏小时，膜面的力学性能被削弱，从而使形面误差较大。

图5 考虑膜材厚度均匀偏差的形面误差分布Fig.5 Shape error distribution considering uniform deviation of membrane thickness

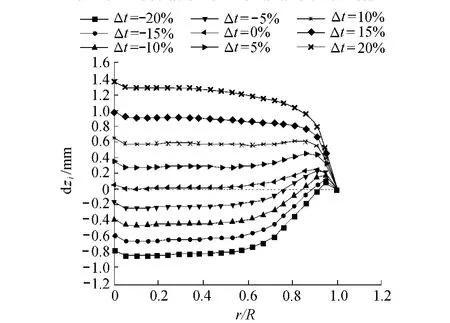
图6 考虑Δt均匀分布时L1的形状偏差Fig.6 Shape error distribution of L1 considering uniform deviation of membrane thickness

图7 各区段内d zi的变异系数Fig.7 Coefficient of variation of d zi in each section

图8 δRMS～Δt均匀分布关系曲线Fig.8 δRMS-Δt of membrane thickness curve

2.2 对不同形状抛物面成形精度的影响

对不同焦径比的抛物面进行成形模拟，分析每种形状在不同膜材厚度偏差均匀分布情况下δRMS(图10)及 δRMS对 Δt的敏感度(图11)。

由图10可以看出:(a)Δt=0时，δRMS值随着F/D增加而增大，这是由于抛物面是由裁剪片拼接后充气而得，裁剪片是不可展曲面，造成未引入误差的情况下也存在一定的成形误差，并且抛物面曲率越大，曲面展开时产生的误差也越大。(b)δRMS随F/D的增大而增大，即抛物面越浅，其成形精度受Δt的影响程度越大，这与毛丽娜等［8］的研究结果吻合。

图9 δRMS～Δt均匀分布的敏感度Fig.9 δRMS-Δt sensitivity to uniform deviation of membrane thickness

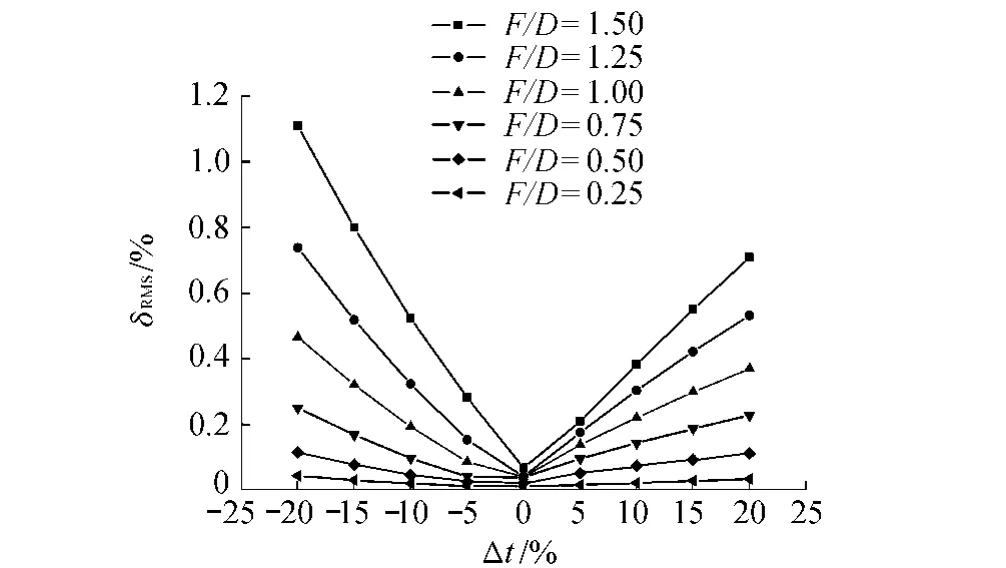
图10 不同形状抛物面δRMS～Δt均匀分布关系Fig.10 δRMS-Δt uniform deviation of membrane thickness curves for paraboloids with different shapes

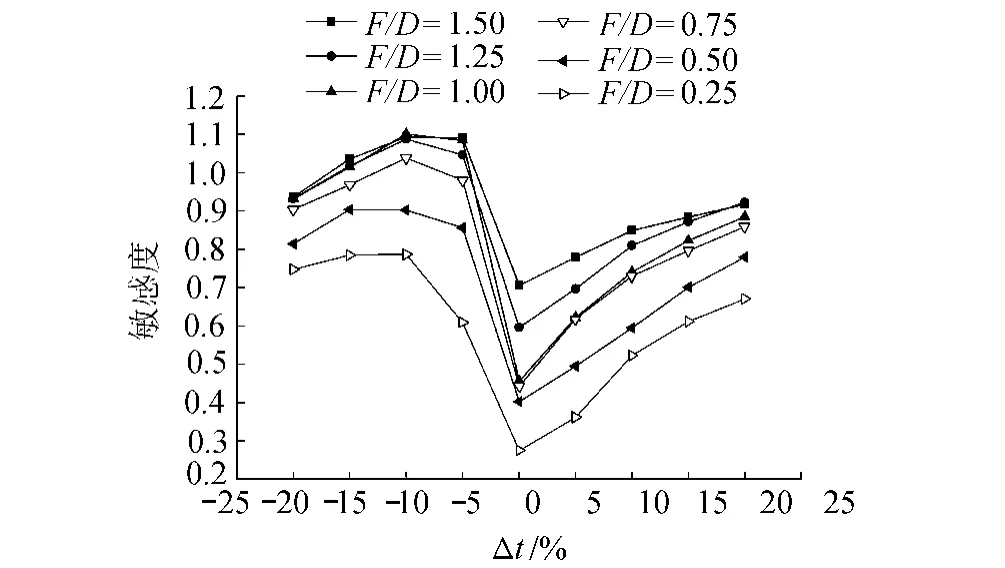
图11 不同形状抛物面δRMS～Δt均匀分布敏感度Fig.11 δRMS-Δt sensitivity to uniform deviation of membrane thickness for paraboloids with different shapes

由图11可以看出:Δt均匀分布时，偏差偏大，δRMS对Δt的敏感度较小;δRMS对Δt均匀分布时的敏感度随着F/D增大而减小。

3 膜材厚度偏差线性非均匀分布对抛物面成形精度的影响

3.1 一般规律

以F/D为1.50的充气抛物面天线为例，对a类和b类膜材厚度偏差线性非均匀分布情况进行分析。=20%时的形面误差分布见图12，曲面形状偏差见图13。由图12、图13可以看出:(a)与膜材厚度偏差均匀分布情况类似，厚度偏小处曲面偏高，厚度偏大处曲面偏低。(b)曲面上各点d zi的变化规律与厚度变化规律对应，也按线性变化。(c)厚度偏差线性非均匀分布时各点d zi曲线与0误差时曲线的交点(A，B)偏向平抛物面中心，并不与厚度变化的交点完全重合。产生此现象的原因是曲线上各点有相互作用，厚度无偏差处受到左右各点的作用也产生了形面误差。(d)与膜材厚度偏差均匀分布相比，偏差线性非均匀分布时曲面形状产生的偏差更小，并且形面误差分布更加均匀。

抛物面在不同膜材厚度偏差线性非均匀分布下的δRMS值见图14。由图14可知:δRMS随着Δt绝对值的增大而增大;当Δt绝对值相等时，偏差线性非均匀分布比均匀分布产生的形面误差小，且b类偏差线性非均匀分布产生的形面误差最小。

图12 =20%时形面误差分布Fig.12 Shape error distribution considering linear non-uniform deviation of membrane thickness

图13 考虑Δt线性非均匀分布时L1的形状偏差Fig.13 Shape error distribution of L1 considering linear non-uniform deviation of membrane thickness

图14 δRMS～Δt线性非均分分布关系Fig.14 δRMS-Δt linear non-uniform deviation of membrane thickness curve

理想抛物面充气膜结构的径向和纬向应力为

式中:P——充气气压;σ1，σ2——充气膜结构的径向和纬向应力;R1，R2——两个主曲率半径。

从式(8)可以看出，从抛物面的中心顶点到边缘，两个方向的应力逐渐增大，并与材料的厚度成反比。当膜材厚度发生从顶点到边缘线性增大的b类变化时，膜面的应力分布更加均匀，与本文b类Δt线性非均匀分布时对抛物面成形精度影响较小的结论相符。

3.2 对不同形状抛物面成形精度的影响

对不同F/D的抛物面进行成形模拟，分析每种形状在不同Δt线性非均匀分布情况下的δRMS(图15)及δRMS对Δt线性非均匀分布时的敏感度(图16)。

图15 不同形状抛物面δRMS～Δt线性非均匀分布关系Fig.15 δRMS-Δt linear non-uniform deviation of membrane thickness curves for paraboloids with different shapes

图16 不同形状抛物面δRMS～Δt线性非均匀分布的敏感度Fig.16 δRMS-Δt sensitivity to linear non-uniform deviation of membrane thickness for paraboloids with different shapes

由图15可以看出:δRMS随着F/D的增大而增大，此现象与Δt均匀分布时类似。Δt线性非均匀分布比均匀分布对抛物面成形精度影响小，并且b类比a类线性变化产生的形面误差小。由图16可以看出:与Δt均匀分布时情况类似，δRMS对Δt线性非均匀分布的敏感度随着F/D增大而减小，但是在敏感度数值上相比，Δt线性非均匀分布的敏感度普遍偏小，说明充气天线抛物面的成形精度对Δt均匀分布更敏感。

4 结 论

采用Fortran语言编译充气抛物面天线有限元分析程序，对6种不同焦径比的反射面进行了成形数值模拟，研究了膜材厚度偏差均匀分布和线性非均匀分布对不同焦距比抛物面成形精度的影响。

a.膜材厚度偏差均匀分布时，抛物面任一母线在区段r/R=0.2～0.6内，形面误差变化不大，此区段可作为反射面有效区域，有利于采取统一措施补偿厚度偏差带来的误差;δRMS随膜材厚度偏差绝对值的增大而增大;由于膜材厚度偏小会削弱膜面的力学性能，因此厚度均匀偏小时形面的δRMS及其敏感度较大。

b.膜材厚度存在偏差线性非均匀分布时，形面误差沿径向按线性分布;δRMS随膜材厚度偏差绝对值的增大而增大;与偏差均匀分布相比，其δRMS值和敏感度都较小;偏差线性非均匀分布b类比a类引起的形面误差更小。

c.与设计曲面相比，在膜材厚度偏小处成形曲面偏高，厚度偏大处曲面偏低。

d.抛物面越浅(焦径比越大)，膜材厚度偏差引起的δRMS越大，因此在设计较浅的反射面时应更加重视膜材厚度偏差对其成形精度带来的影响，严格控制所选膜材的质量;而δRMS对偏差的敏感度则随焦径比增大而减小。

［1］DONALD D J，GREGORY A S.Environmental disturbance modeling for inflatable space structures［C］//43rd AIAA/ASME/ASCE/AHS/ASC Structures.Structural Dynamics，and Materials Conference.Denver，Colorado:AIAA，2002.

［2］NABOULSI S.Investigation of geometric imperfection in inflatable aerospace structures［J］.Journal of Aerospacen Engineering，2004，17(3):98-105.

［3］GRESCHIK G，CASSAPAKISC，VEAL G，et al.Sensitivity study of precision pressurized membrane reflector deformations［J］.AIAA JOURNAL，2001，39(2):308-314.

［4］GRESCHIK G，MIKULASM M，PALISOCA.Approximations and errors in pressurized axisymmetric membrane shape predictions［C］//39th AIAA/ASME/AHS/ASC Structure.Structural Dynamics，and Materials Conference.Washington D C，USA:AIAA，1998.

［5］徐彦，关富玲，管瑜.充气可展天线精度分析和形面调整［J］.空间科学学报，2006，26(4):292-297.(XU Yan，GUAN Fuling，GUAN Yu.Precision analysis and shape adjustment of inflatable antenna［J］.Chinese Journal of Space Science，2006，26(4):292-297.(in Chinese))

［6］徐彦，关富玲，马燕红.充气可展开天线的反射面设计及精度测量［J］.浙江大学学报:工学版，2007，41(11):1921-1926.(XU Yan，GUAN Fuling，MA Yanhong.Reflector design and precision measurement of inflatable antenna［J］.Journal of Zhejiang University:Engineering Science，2007，41(11):1921-1926.(in Chinese))

［7］伞冰冰.膜结构的精细化分析、多目标形态优化与精确成形［D］.哈尔滨:哈尔滨工业大学，2010.

［8］毛丽娜，谭惠丰.充气天线反射面结构的理论分析与精度预测［J］.工程力学，2010，17(4):197-201.(MAO Lina，TAN Huifeng.Stucuture analysis and precision evaluation of inflatable antenna reflector［J］.Engineering Mechanics，2010，17(4):197-201.(in Chinese))

［9］李国强，沈黎元，罗永峰.索结构形状确定的逆迭代法［J］.建筑结构，2006，36(4):74-76.(LI Guoqiang，SHEN Liyuan，LUO Yongfeng.Inverse iteration method in form-finding of cable structures［J］.Building Structure，2006，36(4):74-76.(in Chinese))

［10］杨睿，董石麟，倪英戈.预应力张弦梁结构的形态分析:改进的逆迭代法空间结构［J］.空间结构，2002，8(4):29-35.(YANG Rui，DONG Shilin，NI Yingge.Form-finding analysis of prestressed beam string structures-modified inverse-iteration method［J］.Spatial Structures，2002，8(4):29-35.(in Chinese))

［11］金晓飞，范峰，沈世钊.巨型射电望远镜(FAST)反射面支承结构参数敏感性分析［J］.土木工程学报，2010，43(2):12-19.(JIN Xiaofei，FAN Feng，SHEN Shizhao.Parameter sensitivity analysis of the cable-net structure supporting the reflector of a large radio telescope-FAST ［J］.China Civil Engineering Journal，2010，43(2):12-19.(in Chinese))

［12］章光，朱维申.参数敏感性分析与试验方案优化［J］.岩土力学，1993，14(1):51-57.(ZHANG Guang，ZHU Weishen.Parameter sensitivity analysis and optimizing for test programs［J］.Rock and Soil Mechanics，1993，14(1):51-57.(in Chinese))

［13］姚继涛，解耀魁.既有结构可靠性评定中变异系数统计推断［J］.建筑结构学报，2010，31(8):101-105.(YAO Jitao，XIE Yaokui.Statistical inference for coefficient of variation in reliability assessment of existing structure［J］.Journal of Building Structures，2010，31(8):101-105.(in Chinese))