应用Logistic曲线预测水库垂向水温

许 丹，陆宝宏，程昕野，顾洪宾，3，祁昌军，阮晓波，刘蕊蕊

(1.河海大学水文水资源学院，江苏南京 210098;2.浙江大学能源工程系，浙江杭州 310027;3.中国电力建设集团有限公司，北京 100044;4.环境保护部环境工程评估中心，北京 100012)

水电站大坝建成后，改变了原河流的水力学特性，对于调节性能较高的水库容易形成水温的垂向分层，正确估计水库水温的分布规律对坝工设计、施工期间混凝土坝的温度控制、大坝质量的保证以及坝下游生态环境的保护、低温尾水对生活生产危害的消弭等都具有重要意义［1］。

我国对水库的水温观测始于20世纪50年代，60年代初开始对水库水温特性进行研究，70年代中后期提出了一些水库水温估算的方法，并逐渐将研究成果应用于生产实践。关于水库垂向水温分布的计算，国内已经提出了许多经验方法，最具代表性的有以下4种方法:(a)1985年东北勘测设计院在综合分析国内大量实际观测资料的基础上提出了东北勘测设计院计算公式(简称东勘院法)［2］，该公式较适用于一些中小型水库月平均水温的估计;(b)朱伯芳［3］将水库水温的变化以年为周期，不同深度的水温变化采用余弦函数近似，该方法(简称朱伯芳法)指出温度变化为指数分布，对于典型三层式分布水库预测时，不能很好地反映温跃层的特点;(c)1993年李怀恩［4］采用幂函数型经验公式对水库水温的垂向分布进行模拟，可以较准确地预测水库温跃层的水温分布;(d)1997年中南勘测设计研究院对朱伯芳法的参数进行了统计分析［5］，确定了参数的计算方法，然后在考虑水库的规模和运行方式后再对计算出的参数进行修正。

通过研究发现，Logistic曲线的特征与典型三层式水库垂向水温分布规律相似。因此，笔者采用Logistic曲线模拟水库垂向水温，分析其参数规律，并用于水库垂向水温预测。

1 垂向水温分布公式的建立

1.1 水库水温垂向分布类型

水库水温分布受到诸多因素的影响，如太阳辐射、水库物理特性、入库水量和泥沙等，其水温垂向分布大致可分为3种类型［6］，即混合型(等温型)、稳定分层型和过渡型。混合型水库大多为调节能力较低、水深较浅的水库，由于上、下层水体可进行充分的热量交换，年内不同时间和深度的水温分布都比较均匀，其水温变化与气温有显著的相关关系。稳定分层型水库是指库表水温与库底水温差别明显，上、下层水体不能进行充分的热量交换，一般水深大于40 m，调节能力大的水库。其垂向水温结构可分为3层:上层，即温变层［7］，该层水温受环境温度影响大，随气温变化明显;中层，又称温跃层或斜温层，该层水温随着水深的增加剧烈变化，温度梯度可达1.50℃/m以上［8］;下层，也称滞温层，该层水温基本保持均匀，年内变化很小，常年处于低温状态。过渡型水库是兼有混合型和稳定分层型特征的水库，既可以呈现很强的温跃层，上、下层水体之间也能进行充分的热量交换，年内库底温差很大。

1.2 公式推导

自然界的许多事物都有一个发生、发展与衰亡的过程，但处于不同阶段，其发展速度是不一样的。一般初期处于起始阶段，举步维艰，发展速度缓慢;中期处于生长旺盛阶段，增长迅速;后期处于老化阶段，受到各种条件的制约，增长速度变缓，直至趋于消亡。这一过程若用一条曲线来描述，就是S形增长曲线。S形增长曲线有多种函数表达形式，Logistic曲线是应用最广泛的一种，该曲线方程为

式中k，a，b为Logistic曲线的3个参数(无量纲)，其中a为积分常数。

通过对水库的垂向水温实测资料分析，可知水库垂向分层水温分布与Logistic曲线(图1，参数 k，b，a分别取12，0.2，-6)相似，因此本文采用该方程对水库水温垂向分布规律进行拟合。

Logistic曲线有如下函数性质:

根据Logistic曲线的上述性质以及分层型水库垂向水温的分布特点，在Logistic曲线的基础上，笔者提出如下垂向水温的分布公式:

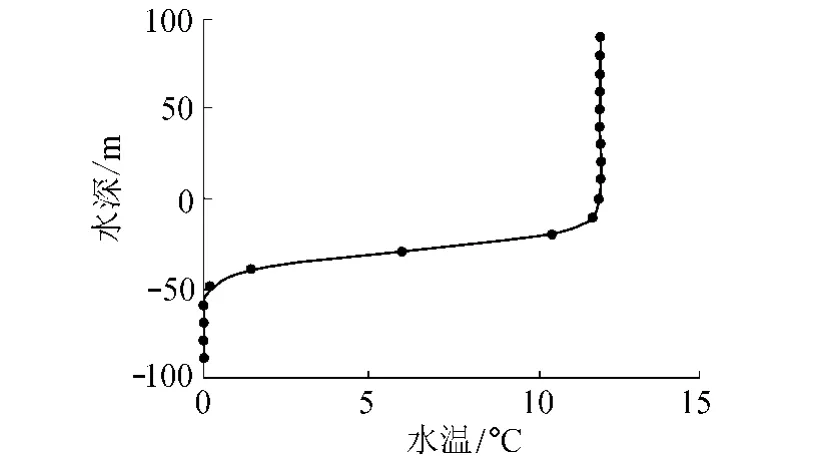
图1 Logistic曲线Fig.1 Logistic curve

式中:T(y)——水深 y 处的水温，℃;y——水深，m;Td——库底水温，℃。

2 参数拟合

2.1 资料选取

新安江水库是一座具有多年调节性能的典型分层型水库，本文采用的水温实测资料为新安江水库2007年的水温垂向分布的人工观测资料。观测时选取平行于坝前170m的一个监测断面，断面长度约为400m，监测断面上共布置4条测温垂线(T1～T4)，垂线间距为100 m。在施测期间，共得到32组数据(16 d，上午和下午各1组数据)。通过对实测资料的分析，得到以下结论:(a)同一测次，4条测温垂线同一深度的水温相差不大;(b)气温日变化对水温垂向分布的影响不明显。鉴于此，为了降低单次测量的偶然误差，选取4条垂线上午和下午2个测次的平均值作为该监测断面的水温垂向分布，得到16组数据，并对这16组数据进行拟合。

2.2 拟合结果

虽然Logistic曲线方程能较好地描述某些有界增长现象，并在预测学、信息科学、生物学、农业学和经济学等领域都有较广泛的应用，但在水库水温预测领域还尚未使用过。

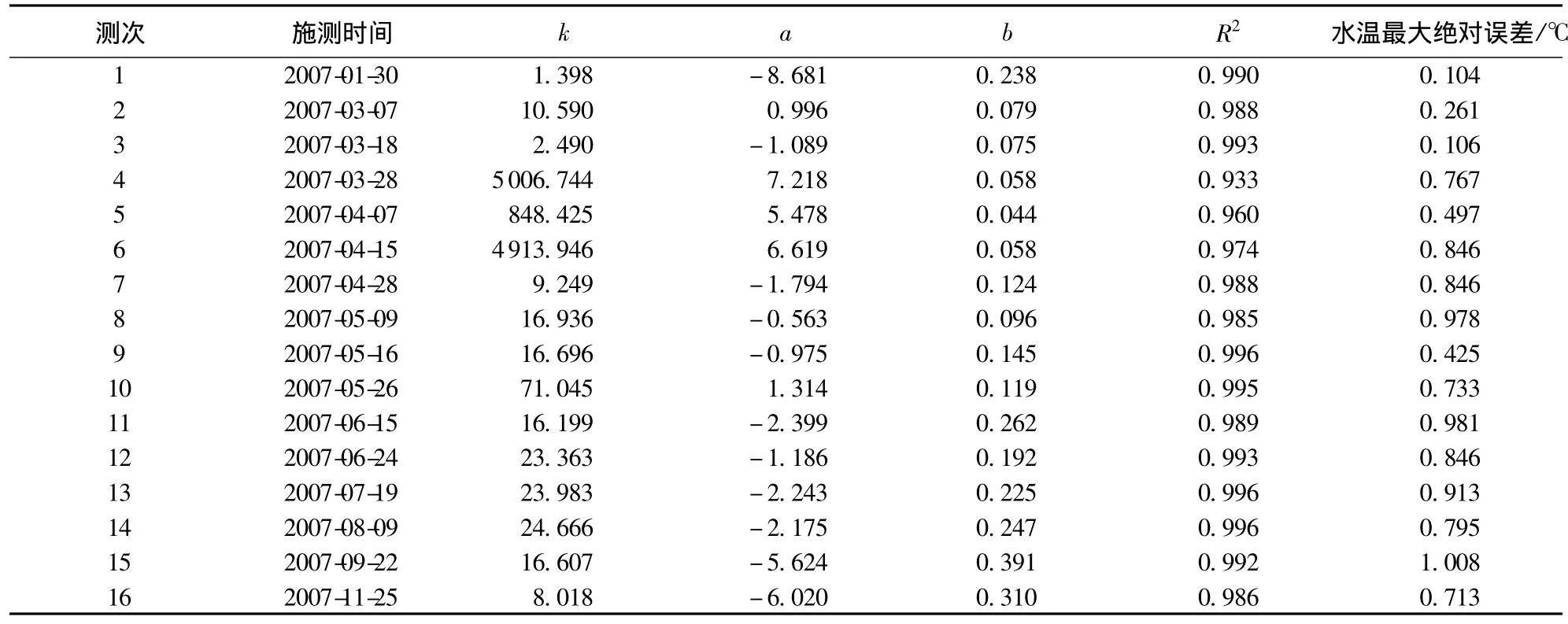
表1 新安江水库Logistic曲线参数优选结果Table 1 Logistic curve parameter optimization results for Xin’anjiang Reservoir

研究结果表明，模型的参数选取直接影响模型的预测精度。式(3)的4个参数中，k，a，b完全取决于Logistic曲线方程。学者们对该3个参数也提出了许多估算方法。章元明等［9］总结了前人的研究成果，得出Logistic曲线方程的3类共16种参数估计方法，其中应用较广泛的有三点法、差分法、灰色建模法和0.618法等，但计算工作量较大;董江水［10］提出用SPSS软件中的非线性回归拟合Logistic曲线的方法和步骤。非线性回归的方法对参数初值的要求低，即使参数初值选取不准确，仅影响迭代次数和计算时间，不影响参数的最优解，而且操作简单。笔者采用SPSS软件中的非线性回归方法对Logistic曲线方程参数进行拟合。

根据新安江水库水温实测资料，对Logistic曲线方程参数进行优选，结果见表1。其中，R2表示拟合优度，拟合优度越接近1，说明拟合效果越好。由表1可知，R2值接近于1，说明拟合效果很好。各测次实测值与计算值对比见图2。限于篇幅，只给出部分测次的实测和模拟水温对比。

从模拟结果上看，本文提出的Logistic曲线水温预测公式能很好地反映新安江水库水温垂向的分布情况，尤其能反映典型三层式分层水库温跃层的特点，预测精度较高，水温实测值和预测值最大绝对误差为1.008℃。

图2 新安江水库水温实测值与计算值对比Fig.2 Comparison of measured and calculated water temperature in Xin’anjiang Reservoir

3 适用性分析

为研究Logistic曲线水温预测公式的适用性，笔者利用丹江口水库多年月平均水温资料、黄冈水库资料［11］和冯家山水库资料［4］对公式进行拟合，结果见图3～5。根据实际数据，黄冈水库2007年10月23日的拟合误差最大为0.7℃，误差在可接受范围。误差较大的原因是测试仪器(声速剖面仪)受环境温度影响，入水时未在表层水中停留所致。应用东勘院法和朱伯芳法对丹江口水库月平均水温进行计算，与本文经验公式的结果对比见图6。由图6可知:东勘院法虽能够较准确地反映温跃层特点，但是误差较大;朱伯芳法计算误差较大且不能准确表现温跃层特点［12］;笔者提出的经验公式能准确地反映温跃层的特点且误差较小。

图3 丹江口水库月平均水温实测值与计算值对比Fig.3 Comparison of measured and calculated monthly average water temperature in Danjiangkou Reservoir

根据分析可以得到以下结论:

a.经验公式(式(3))的拟合精度较高，对不同区域、不同规模和调节性能的水库水温模拟效果较好。限于资料，笔者仅对上述4个水库进行了验证，结果表明，该公式适用范围较广，对于不同时期(升温期(图2(a)中的3条线和图3中3月、4月2条线)，稳定分层期(图2(c)中3条线和图3中7—10月4条线))，以及不同垂向分布类型的水库(混合型(丹江口水库)、稳定分层型(新安江水库))都有很好的适用性。

b.由 Logistic曲线的性质［13］可知，点(a/(-b)，k/2)为曲线的拐点，用于水温预测即为温跃层中心点，a/(-b)即为温跃层中心点的水深。从计算结果看，丹江口水库4月份(a/(-b)=0.86)至9月份(a/(-b)=26.30)，a/(-b)值呈现逐渐增大的趋势，这个结论与文献［5］的结论是一致的。对于新安江水库，由于是单次的实测结果，影响因素很多，造成参数的规律性不甚明显。

图4 黄冈水库水温实测值与计算值对比Fig.4 Comparison of measured and calculated water temperature in Huanggang Reservoir

c.采用SPSS软件拟合公式参数，应用简单、效率高，计算结果可靠。

4 预测应用

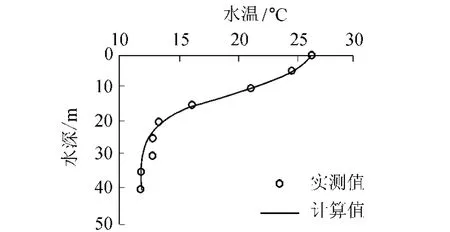
图5 冯家山水库2007年8月份月平均水温实测值与计算值对比Fig.5 Comparison of measured and calculated monthly average water temperature in Fengjiashan Reservoir in August，2007

分析结果表明，Logistic曲线水温预测公式对不同区域、规模和调节性能的水库具有较好的适用性，且预测精度较高。公式中各参数选取直接影响预测结果的精度。

4.1 库底水温T d的确定

对于无水温实测资料的水库，学者们已提出很多可借鉴的方法，如文献［2］，［4］和［5］提到的方法。

4.2 参数k，a，b的确定

无水温实测资料的水库，已知的只是水库的规模(水深、库容、来水量等)以及水库的地理位置、气候类型等，其参数确定有以下2种途径:首先，可以直接移用有实测资料的相似水库的优选参数;此外，还可以通过以下方法确定参数。

图6 经验公式计算结果对比(丹江口水库5月和8月月平均水温)Fig.6 Comparison of calculated results of empirical formulas(monthly average water temperature in Danjiangkou Reservoir in May and August)

a.由计算结果可知参数b的变化范围很小(新安江水库参数b的变化范围为0.044～0.391，丹江口水库4—10月参数b的变化范围为0.117～0.222)，因此可根据地域和季节，取参数b为常数。取丹江口水库的参数b=0.150，新安江水库的参数b=0.200。参数k和a仍采用优化的结果。丹江口水库和新安江水库参数计算结果见表2和表3。计算结果表明，参数b取常数后，新安江水库水温计算最大绝对误差为2.723℃，丹江口水库为1.07℃，水温计算值在可接受范围内。因此，参数b取定值是可行的，预测时可根据有实测资料的相似水库参数b的取值范围确定一个定值b。

表2 丹江口水库5月、6月水温垂向分布Table 2 Vertical distribution of water temperature in Danjiangkou Reservoir in May and June

表3 新安江水库b=0.200时的计算结果Table 3 Calculated results of Xin’anjiang Reservoir when b=0.200

Tb可以根据现有的方法［2］估算。参数k反映温跃层中心点的水温，经分析发现k与前期时段平均气温存在相关关系，且前期时段气温时间序列越长其相关关系越好，2007年3月7日至8月9日的13个参数k与前30日平均气温的相关系数为0.979。

b.根据式(3)，当y=0时库表水温Tb存在如下关系:

笔者选取了新安江水库附近地区气象站点(杭州站、黄山站、道孚站)以及新安江尾水气温共4组数据进行分析，结果表明，参数k与尾水气温的相关性最好。因此，在进行计算时推荐采用库区实测气温，这样得到的相关关系会更好。本文结果与李怀恩［4］对丹江口水库和冯家山水库的分析结论一致。实际应用时，除了直接移用参数外，还可以移用参数k与气温的相关关系，并根据预测水库的气象条件对参数k进行修正。

c.a/(-b)为温跃层中心点的水深，从理论上讲，其变化规律如下:从升温期开始，温跃层中心点的水深逐渐增大。从丹江口水库的计算结果看，该规律比较明显。因此，可建立其与月份的关系，可均匀变化，也可根据相似的有实测资料水库的参数，采用相应的变化规律［5］。此外，如果参数k确定后，反推出参数a(式(5))，便可运用式(3)进行计算。

5 结 语

提出了利用Logistic曲线估算垂向水温分布的新方法。Logistic曲线水温预测公式有如下特点:(a)拟合精度较高，适用性较强，具有可行性;(b)对于有实测资料的水库，参数计算方法简单且可靠性高;(c)对于无实测资料的水库，参数可由本文提出的途径来估计，且能满足精度要求。Logistic曲线水温预测公式需要确定4个参数，分析结果表明其中3个参数k，a，b具有一定的规律性，但限于实测水温难以获得，目前尚无法对各参数的规律性一一总结定性。下阶段将通过收集更多不同类型水库的水温实测资料，分析公式参数的规律性，完善Logistic曲线水温预测公式的适用性，为我国水库水温预测增添一种可选方法。

［1］陆宝宏，王春燕，王瑞巧，等.二滩水库温度原型测试定位误差初探［J］.水利学报，2007，38(增刊1):535-541.(LU Baohong，WANG Chunyan，WANG Ruiqiao，et al.Position error analysis associated archetypal measurement about water temperature and velocity fields in Ertan Reservoir［J］.Journal of Hydraulic Engineering，2007，38(Sup1):535-541.(in Chinese))

［2］SLD 214—1983 水利水电工程环境影响评价规范［S］.

［3］朱伯芳.库水温度估算［J］.水利学报，1985，16(2):12-21.(ZHU Bofang.The reservoir water temperature estimation［J］Journal of Hydraulic Engineering，1985，16(2):12-21.(in Chinese))

［4］李怀恩.分层型水库的垂向水温分布公式［J］.水利学报，1993，24(2):43-49，56.(LI Huaien.The vertical water temperature distribution formula of stratified reservoir［J］.Journal of Hydraulic Engineering，1993，24(2):43-49，56.(in Chinese))

［5］岳耀真，赵在望.水库坝前水温统计分析［J］.水利水电技术，1997，28(3):2-7.(YUE Yaozhen，ZHAOZaiwang.Statistical analyses of reservoir water temperature near upstream dam face［J］.Water Resources and Hydropower Engineering，1997，28(3):2-7.(in Chinese))

［6］张研，苏国韶，燕柳斌.水库水温分布结构识别的高斯过程机器学习方法［J］.水利水电科技进展，2009，29(2):13-15，39.(ZHANG Yan，SU Guoshao，YAN Liubin.Study on Gaussian process machine learning method for identifying the distribution structure of reservoir water temperature［J］.Advances in Science and Technology of Water Resources，2009，29(2):13-15，39.(in Chinese))

［7］COATSK，DEMPSEY J，HENDERSON J.The use of vertical equilibrium in two-dimensional simulation of three-dimensional reservoir performance［J］.Society of Petroleum Engineers Journal，1971，11(1):63-71.

［8］张大发.水库水温分析及估算［J］.水文，1984(1):19-27.(ZHANG Dafa.Analysis and estimation of reservoir water temperature［J］.Journal of China Hydrology，1984(1):19-27.(in Chinese))

［9］章元明，盖钧镒.Logistic模型的参数估计［J］.四川畜牧兽医学院学报，1994，8(2):46-51.(ZHANG Yuanming，GAI Junyi.Parameter estimation of Logistic model［J］.Journal of Sichuan Institute of Animal Husbandry and Veterinary Medicine，1994，8(2):46-51.(in Chinese))

［10］董江水.应用SPSS软件拟合Logistic曲线研究［J］.金陵科技学院学报，2007，23(1):21-24.(DONG Jiangshui.Study on fitting Logistic curve with SPSSsoftware［J］.Journal of Jinling Institute of Technology，2007，23(1):21-24.(in Chinese))

［11］杜惠锦.黄岗水库水温变化规律的探讨［J］.水资源保护，1987，2(2):26-32.(DU Huijin.The study of water temperature changes of Huanggang reservoir［J］.Water Resources Protection，1987，2(2):26-32.(in Chinese))

［12］杨梦斐，李兰，李亚农，等.规范推荐的水库水温经验预测方法比选研究［J］.水资源保护，2011，27(5):55-58，105.(YANG Mengfei，LI Lan，LI Yanong，et al.Comparison study of recommended empirical prediction methods for reservoir water temperature in specification［J］.Water Resources Protection，2011，27(5):55-58，105.(in Chinese))

［13］朱正元，陈伟侯，陈丰.Logistic曲线与 Gompertz曲线的比较研究［J］.数学的实践与认识，2003，33(10):66-71.(ZHU Zhengyuan，CHEN Weihou，CHEN Feng.Comparisons on Logistic curve and Gompertz curve［J］.Mathematics in Practice and Theory，2003，33(10):66-71.(in Chinese))