改进的TOPSIS综合评价模型在河道整治方案优选中的应用

徐存东，翟东辉，张 硕，胡 丹

(华北水利水电大学水利学院，河南郑州 450011)

河道整治方案选择的优劣会直接影响河流健康和流域的和谐发展，是关系流域长远发展与河流安全的大事，因此采用合适的优选方法、模型评估河道整治方案的优劣具有重要意义［1］。近年来，西方发达国家在河流整治方案评估方面做了大量工作，取得了显著成效，其实践结果具有一定的代表性［2-4］;而国内河道整治方案评价工作尚处于起步阶段，缺乏统一的评价指标体系和可操作的定量评价模型［5］。

目前，属性识别理论、人工神经网络模型、模糊多属性决策模型［5］等综合评价方法已经应用到河道整治方案的优选中，对河道整治方案的优选和评估工作起到了积极作用。但实践证明这些方法都存在一定的局限性，如属性识别评价模型在对多个因子赋权时的工作量大，且未考虑多个评价指标之间的联系［6］;人工神经网络和模糊多属性决策模型存在评价精度不高、影响因素的权重确定困难等问题［7］。笔者尝试将改进的TOPSIS综合评价模型引进河道整治方案优选中，建立乌海市摩尔沟河道整治方案优选评估的TOPSIS模型。该TOPSIS模型利用信息熵权法反映和评估了指标权重的重要性，并充分发掘评估指标的特性，将人为主观因素的影响降到最低限度，为河道整治方案研究提供一条新思路。

1 传统TOPSIS模型

TOPSIS法是Hwang等在1981年提出的一种以有限个评价对象和理想化目标接近程度为依据的排序方法［8-10］。它通过对原始数据矩阵进行同趋势化和归一化处理来消除不同指标量纲的影响，找出各方案中最优、最劣方案，并分别计算各个评价对象与最优方案之间的相对贴近度，以此作为评价方案优劣的依据，实现有限个方案与多个决策目标之间的综合评价［11］。传统TOPSIS模型存在如下缺陷:

a.方案评价中可能会出现评价结果与理想解、负理想解的欧氏距离同样接近的情况，此时按照相对欧式距离排序则不能充分体现各方案的优劣程度［12-14］。另外，各个评价指标之间的信息重复亦会影响评价结果的准确性。

b.各评价指标权重一般先通过专家评价法、德尔菲法(Delphi)或层次分析法(AHP)确定［15］，但其主观因素较多，具有一定的局限性，通常无法准确反映方案评价指标的真实性。

基于传统TOPSIS模型的不足，笔者提出基于熵权的改进TOPSIS综合评价模型，并将其引进河道整治方案优选评估中，为河道整治方案优选提供一条新思路。改进的TOPSIS综合评价模型可避免传统TOPSIS模型的一些缺陷，能够客观、准确地对方案进行优选评价。

2 传统TOPSIS模型的改进:正交投影法

针对传统TOPSIS模型的a项缺陷，引进“垂面距离”来代替欧氏距离，以避免评价结果与理想解、负理想解的欧氏距离同样接近的弊端。

2.1 改进思路

2.1.1 引入“垂面距离”

假设评估指标体系中有3个评价指标x，y，z，如图1所示点A(x+，y+，z+)对应理想解向量，点B(x-，y-，z-)对应负理想解向量，G(x1G，y1G，z1G)，H(x1H，y1H，z1H)，E(x1E，y1E，z1E)，F(x1F，y1F，z1F)分别为 4 个方案对应的样本点，过点H，G和E，F分别作垂直于AB的直线，垂足为点C、点D。传统TOPSIS模型得到的评优结果为G优于H，E优于F，前后明显存在矛盾。实际上，虽然G比H更贴近A，但同时也更接近B。由图1可知，沿直线HG，方案由H向G靠近的过程中贴近A与B的程度相同，即H与G的排序结果相同，同理E与F的排序结果也相同。由此可见，利用传统TOPSIS模型的欧氏距离计算相对贴近度可能得不到合理结果［10］。因此，笔者尝试引进“垂面距离”代替欧氏距离，对传统的TOPSIS模型进行改进。

“垂面距离”的含义是指在理想解与负理想解之间存在两点，分别过这两点作以理想解与负理想解连线为法向量的平面之间的距离［16］。如图1所示，A，B分别是有限评估方案(对于有限个方案的决策分析而言，理想解与负理想解是存在的)所得到的理想解与负理想解。图中G，F两点的“垂面距离”是指分别经过点G与点F且均以直线AB为法向量的两平面间的距离。即平面a1b1c1d1与a2b2c2d2之间的距离——点G和F分别在直线AB上的正交投影点C和D间的欧氏距离。另外，容易证明，与理想解“垂面距离”近的方案与负理想解的“垂面距离”远［16］。

2.1.2 熵权法计算指标权重

采用熵权法确定河道整治方案优选的指标权重时，某项指标对决策作用越大则说明该指标携带和传送的信息越多，因此可用信息熵来评判所获得的系统信息效用及其有序程度［17-18］。即通过评价指标值所构成的判断矩阵确定指标权重，能够消除人为主观因素的干扰，使评价结果更客观合理。

假设有m个方案与n项评价指标，利用熵权法确定指标权重的公式为

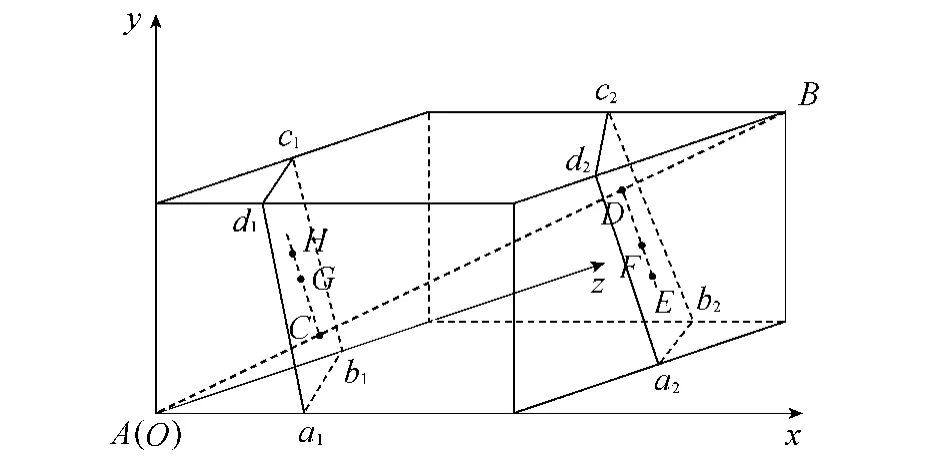
图1 TOPSIS模型的“垂面距离”示意图Fig.1 Schematic diagram of vertical distance in TOPSIS model

其中

式中:Hj——第j项评价指标的熵;fij——第i个方案第j项指标的评价值所占的比重;bij——第i个方案第j项评价指标的评价值。

在实践中，为使In fij有意义，一般需假设:当fij=0时，fijIn fij=0。但当fij=1时，亦有fijIn fij=0，因此上述假设显然与实践不符，与熵理论相悖，故对fij进行如下修正:

评价指标的熵权W为

其中

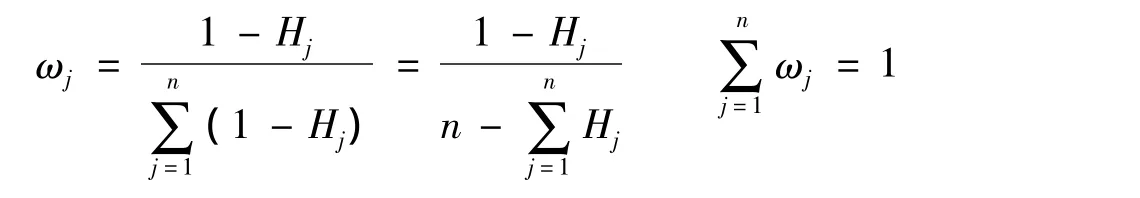
式中:ωj——第j项评价指标的熵权;1-Hj——第j项指标的差异系数，即第j项指标的熵值越小，表明该指标值的变异程度越大。

2.2 改进的TOPSIS综合评价模型的建立

2.2.1 建立决策矩阵X

假设多项指标决策问题的方案集、指标集分别为M=(M1，M2，…，Mm)，C=(C1，C2，…，Cn)。方案 Mi在指标Cj下取值为xij，则形成多目标的决策矩阵为

2.2.2 建立标准化判断矩阵V

将X进行归一化处理，得到标准化的判断矩阵V=(vij)m×n。

对于效益(即越大越优)型指标:

对于成本(即越小越优)型指标:

式中xjmax，xjmin分别为第j项评价指标在决策方案中的最大值与最小值。

2.2.3 构建加权决策矩阵R

利用熵权法计算出的ωj与V相乘构建加权决策矩阵R=(rij)m×n，其中

2.2.4 计算理想解S+与负理想解S-

第j项指标的理想解为

为简化计算，将坐标原点平移至理想解点，且平移矩阵为T=(tij)m×n，其中

2.2.5 “垂面距离”的计算

设图1 中点 C，D，G，F 对应的向量分别是 c，d，g，f，则 G，F 点的“垂面距离”为

各方案的S+与S-之间的距离‖c-d‖为常数，故只需计算(c-d)·(g-f)，则各个方案与S+间的“垂面距离”为

式中:p——经过步骤2.2.4平移过后的理想解，即零向量;q——平移后的负理想解;Ti——矩阵T的第i个行向量，化简式(11)得

3 实例分析

以北方地区乌海市摩尔沟河道整治方案的优选为例［15］，阐述改进的TOPSIS模型在河道整治方案优选中的应用。

乌海市位于内蒙古自治区东南，属于典型的大陆型气候，摩尔沟河从乌海市北部流入，经主城区后散漫流入黄河。摩尔沟河上游长5.5km，左、右岸分别为城区和荒山，河道比降较大，通常情况下河槽几乎全部干涸;中游长4.5km，两岸均为城市中心区，河道比降介于上、下游之间;下游长1.5km，两岸均属于黄河湿地区域，河道比降较缓。整个河道岸坡基本处于自然状态，河道淤积严重、蓄水能力差、防洪水平低等问题严重威胁当地人民群众的生命财产安全。为从根本上解决存在问题，当地相关部门决定对摩尔沟河道进行整治，拟将其建设为集生态、防洪、景观、供水为一体的多功能现代化河道，整治范围自东山截洪沟至黄河游龙湾滨河湿地区域，总长约11.5 km。

3.1 河道整治评估指标体系的建立

河道整治的关键是对河道断面和护坡形式进行优选。考虑到城市防洪、生态、供水等功能要求，拟定以下4项河道整治方案［19］。

方案Ⅰ:全河段为单槽断面(沿河道修建拦河蓄水的水闸或橡胶坝，以便充分利用水资源)，护坡材料为干砌石，只有便于行洪的洪水槽，如图2(a)所示。

方案Ⅱ:全河段采用双槽断面，护坡材料为浆砌石，一侧为洪水槽(在洪水槽内修建拦河蓄水的水闸或橡胶坝)，另一侧为清水槽，中间设中隔墩，行洪较好，运行管理难度较低，如图2(b)所示。

方案Ⅲ:全河槽为三槽断面，护坡材料采用混凝土，两侧布置清水槽，中间布置洪水槽，设2道中隔墩，在景观效果方面可实现双侧亲水，同时兼顾未来发展，如图2(c)所示。

方案Ⅳ:上游为双槽断面、中游为三槽断面、下游为单槽断面。

河道整治工程方案的评估指标众多，选取指标应遵循科学、系统、简明的原则，并依据现代河道整治规划理念。由于决策方案属性的多样性，目前尚无万能的决策指标体系，所以在遇到具体的决策问题时需根据实际情况建立适宜的决策指标体系。笔者结合乌海市地区的实际情况，将摩尔沟河道整治方案的优选模型拟定评价准则定为社会效益、生态效益、经济效益三方面［20］，评价指标体系结构见表1。

图2 河道单槽、双槽、三槽模式断面示意图Fig.2 Schematic diagram of river cross-sections with single，double，and triple channels

表1所示指标体系的构建考虑了河道整治的“社会-生态-经济”综合效益耦合关系，能够较全面地反映现代河道整治的理念。其中“洪水资源利用率”反映了利用洪水资源的能力，与当地生产、生活相关;“占地面积”反映了土地资源的合理利用水平;“与环境协调性能”体现了工程与周围环境相协调的重要性;“亲水性能”反映了人类活动的原则，是坚持以人为本、人水和谐的表现;“投资成本”和“土地增值效益”反映了水利工程的经济统筹性原则。

3.2 确定评价指标并建立模型

为确定最佳河道整治方案，从投资成本、亲水性能、环境协调性能、占地面积、洪水资源利用率、土地增值效益6个指标进行综合评估，河道整治方案总体评估指标值见表2。亲水性能与环境协调性能指标值通过专家打分法获得。投资成本、占地面积2个指标为成本型指标，数值越小越好;其他4个均为效益型指标，数值越大越好。

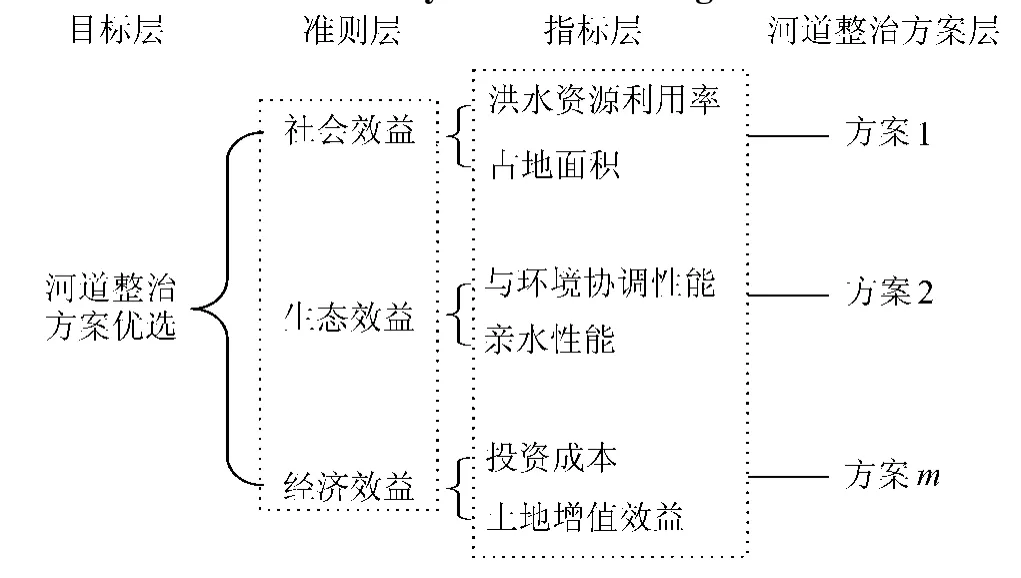
表1 河道整治工程评价指标体系Table 1 Evaluation index system of river regulation schemes

表2 河道整治方案总体评估指标数值Table 2 Values of comprehensive evaluation indices of river regulation schemes

3.3 熵值法计算权重

对表2中提供的原始信息经过无量纲和正向化处理［21-22］，得到表3，将表3结果作为各方案综合评估的样本值代入式(1)～(3)，利用熵值法计算评估指标的权重向量W=(0.471 1，0.139 4，0.152 7，0.083 5，0.0447，0.1086)。

表3 河道整治方案总体评估数值无量纲化和正向处理结果Table 3 Normalized and positive management results of comprehensive evaluation indices of river regulation schemes

3.4 引进正交投影法计算各方案评估值

根据式(5)、式(6)及已计算出的W，利用正交投影法评估各方案的优劣(各指标权重系数均乘以100;容易证明，所有的指标权重系数都乘以同样的正数，正交投影法的计算结果将扩大正数的平方倍，并不会影响各方案排序［14］)，构建河道整治方案加权决策矩阵如下:

对R进行坐标变换得坐标轴平移后的矩阵为

由式(10)～(12)得各方案的“垂面距离”为 D1=2 854.491 6，D2=1 826.157 5，D3=645.343 2，D4=40.7127。

正交投影法的评估结果显示，乌海市河道整治各方案优劣顺序为:方案Ⅳ＞方案Ⅲ＞方案Ⅱ＞方案Ⅰ，易知方案Ⅳ所带来的预期综合效益最大。改进后的TOPSIS综合模型评价结果与AHP-FCM模型评估结果一致［23］，说明改进后TOPSIS综合评价模型具有可行性。

传统TOPSIS评价模型计算得出的结果为:C=(0.4768，0.6549，0.9982，0.9341)，其优劣顺序为:方案Ⅲ＞方案Ⅳ＞方案Ⅱ＞方案Ⅰ，与改进的TOPSIS综合评价模型计算结果存在显著差别。

3.5 结果分析

摩尔沟河道上游左岸是乌海市景观质量要求较高的城区。在汛期单槽模式需要提前全部塌坝或坍平运行，会导致河槽全部变为干河槽，景观效果变差。清水槽修建在左岸可明显改善城市面貌，而右岸为荒山，且有上游洪水汇流入摩尔沟;若清水槽修建在右岸，则上游洪水会挟带着泥沙进入洪水槽，因此需要修建一段涵洞以跨过清水槽，这样与水利工程的经济性原则相悖。所以双槽模式是上游河道整治的最佳选择。

中游河段两岸为主城区，三槽方案中2个清水槽均位于岸边，可实现双侧亲水的景观效果;而位于中间的泄水槽可使亲水岸线避免僵硬，更加符合美观要求，为乌海市创造人水和谐的生态环境。三槽模式在社会、经济效益上表现也较好，故三槽模式是中游的合理选择。

摩尔沟河道下游河道比降较缓，两岸是被称为“地球之肾”的黄河湿地，具有很好的调节气候、涵养水源、净化水体等功能，将其规划为湿地公园，可满足当地群众日常生活的休闲需求。单槽模式在下游防洪能力强，造价低，且易运行管理。因此，下游选择单槽模式是合理的。

综上所述，河道整治方案Ⅳ客观、完备，符合实际情况，说明改进后的TOPSIS综合评价模型计算结果合理、可行。

4 结 语

在河道整治研究现状分析的基础上，从河道整治的现代理念出发，采用正交投影法对传统TOPSIS模型进行改进，引入“垂面距离”概念对河道整治方案进行决策，建立了河道整治方案优选评估的TOPSIS模型。利用信息熵权法确定评估指标的客观权重，将人为主观因素的干扰降到最低限度，有效避免了以往确定指标权重的主观性。案例计算结果表明改进后的TOPSIS综合评价模型科学合理、简单，结果分析符合实际情况。

在评估TOPSIS模型的指标权重确定时，占地面积、亲水性能和环境协调性能的权重系数较大，在方案优选过程中起关键性作用，体现了河道整治方法优选时人水和谐、生态河流的重要性;将该决策模型用于摩尔沟河道整治方案的优选，其评估结果符合当地的实际情况，说明改进后的TOPSIS综合评价模型合理可行。因此，将改进的TOPSIS综合评价模型用于河道整治方案的优选评估，是对河道方案评估研究的一个拓展，具有良好的应用前景和推广价值。

［1］钱正英，陈家琦，冯杰.人与河流和谐发展［J］.河海大学学报:自然科学版，2006，34(1):1-5.(QIAN Zhengying，CHEN Jiaqi，FENG Jie.Harmonious development between humanity and rivers［J］.Journal of Hohai University:Natural Sciences，2006，34(1):1-5.(in Chinese))

［2］KARR JR，CHU E W.Sustaining living rivers［J］.Hydrobiologia，2000，422/423(0):1-14.

［3］SMITH M J，KAY WR，EDWARDD H D，et al.AUSRIVAS:using macroinvertenrates to assess ecological condition of rivers in Western Australia［J］.Fresh Biology，1999，41(2):269-282.

［4］HART B T，DAVIESPE，HUMPHREY CL，et al.Application of the Australian river bioassessment system(AUSRIVAS)in the Brantas River，East Java，Indonesia［J］.Journal of Environmental Management，2001，62(1):93-100.

［5］高学平，赵世新，张晨，等.河流系统健康状况评价体系及评价方法［J］.水利学报，2009，40(8):962-968.(GAO Xueping，ZHAO Shixin，ZHANG Chen，et al.Index system and method for assessing the health status of river［J］.Journal of Hydraulic Engineering，2009，40(8):962-968.(in Chinese))

［6］程乾生.属性识别理论模型及其应用［J］.北京大学学报:自然科学版，1997，33(1):12-20.(CHENG Qiansheng.Attribute recognition theoretical model with application［J］.Acta Scientiarum Naturalium Universitatis Pekinensis，1997，33(1):12-20.(in Chinese))

［7］殷峻暹，陈守煜.基于相关性分析的多目标模糊优选模型及应用［J］.水电能源科学，2004，22(2):23-26.(YIN Junxian，CHEN Shouyu.Fuzzy decision-making analysis theory and application based on index relativity-analysis［J］.Water Resources and Power，2004，22(2):23-26.(in Chinese))

［8］HWANG C L，YOON K.Multiple attribute decision making:methods and applications，a state of the art survey［M］.Berlin:Springer-Verlag，1981.

［9］林齐宁.决策分析［M］.北京:北京邮电大学出版社，2002.

［10］屈吉鸿，陈南祥，黄强，等.改进的逼近理想解在地下水资源承载力评价中的应用［J］.水利学报，2008，39(12):1309-1314.(QU Jinghong，CHEN Nanxiang，HUANG Qiang，et al.Improved TOPSIS method for evaluating groundwater carrying capacity［J］.Journal of Hydraulic Engineering，2008，39(12):1309-1314.(in Chinese))

［11］陈雷，王延章.基于熵权系数与TOPSIS集成评价决策方法的研究［J］.控制与决策，2003，18(4):456-459.(CHEN Lei，WANG Yanzhang.Research on TOPSISintegrated evaluation and decision method based on entropy coefficient［J］.Control and Decision，2003，18(4):456-459.(in Chinese))

［12］于洋，李一军.基于多策略评价的绩效指标权重确定方法研究［J］.系统工程理论与实践，2003，23(8):8-15.(YU Yang，LI Yijun.Research on giving weight for performance indicator based on the multi-strategy method［J］.Systems Engineering-Theory＆Practice，2003，23(8):8-15.(in Chinese))

［13］KAO C，LIU ST.Fractional programming approach to fuzzy weighted average［J］.Fuzzy Sets and Systems，2001，120:435-444.

［14］胡永宏.对TOPSIS法用于综合评价的改进［J］.数学的实践与认识，2002，32(4):572-575.(HU Yonghong，The improved method for TOPSISin comprehensive evaluation［J］.Mathematics in Practice and Theory，2002，32(4):572-575.(in Chinese))

［15］郑斌，唐德善，史兹国.基于综合集成赋权法的河道整治方案优选研究［J］.水力发电学报，2010，28(4):113-115.(ZHENG Bin，TANG Deshan，SHI Ziguo.Scheme optimization of river regulation based on combination weighting method［J］.Water Resources and Power，2010，28(4):113-115.(in Chinese))

［16］华小义，谭景信.基于“垂面”距离的 TOPSIS法:正交投影法［J］.系统工程理论与实践，2004，24(1):114-119.(HUA Xiaoyi，TAN Jingxin.Revised TOPSIS method based on vertical projection distance-vertical projection method［J］.Systems Engineering-Theory＆Practice，2004，24(1):114-119.(in Chinese))

［17］邱莞华.管理决策与应用熵学［M］.北京:机械工业出版社，2002.

［18］闫文周，顾连胜.熵权决策法在工程评标中的应用［J］.西安建筑科技大学学报，2004，36(1):98-100.(YAN Wenzhou，GU Liansheng.Application of the method of entropy proportion in the engineering mark［J］.Journal of Xi’an University of Architecture＆Technology，2004，36(1):98-100.(in Chinese))

［19］高永胜，王浩，王芳.河流健康生命评价指标体系的构建［J］.水科学进展，2007，18(2):16-18.(GAO Yongsheng，WANG Hao，WANG Fang.Construction of evaluation index system for river’s healthy life［J］.Advances in Water Science，2007，18(2):16-18.(in Chinese))

［20］董哲仁.试论生态水利工程的基本设计原则［J］.水利学报，2004，35(10):1-6.(DONG Zheren.On the design principles of eco-hydraulic engineering［J］.Journal of Hydraulic Engineering，2004，35(10):1-6.(in Chinese))

［21］王晓军.多指标综合评价中指标无量纲化方法的探讨［J］.人口研究，1993(4):47-51.(WANG Xiaojun.A study of nondimensional in multi-indexes comprehensive evaluation［J］.Population Research，1993(4):47-51.(in Chinese))

［22］沈振锋，许炎生，赵慧，等.无量纲化方法在大学生综合测评中的应用研究［J］.华中农业大学学报:社会科学版，2005(2):98-101.(SHEN Zhenfeng，XU Yansheng，ZHAOHui，et al.A study on the application of non-dimensional approaches in the comprehensive evaluation of university students［J］.Journal of Huazhong Agricultural University:Social Sciences Edition，2005(2):98-101.(in Chinese))

［23］丁亿凡，唐德善.西北城市河道整治模式优选研究［J］.河海大学学报:自然科学版，2010，38(5):527-531.(DING Yifan，TANG Deshan.Optimization of training patterns of urban river in China’s northwestern cities［J］.Journal of Hohai University:Natural Sciences，2010，38(5):527-531.(in Chinese))