数字信号处理中的最小相位系统初探

陶 丹，陈后金

(北京交通大学电子信息工程学院国家电工电子实验教学中心，北京100044)

最小相位系统在信号处理等相关领域应用广泛，如同态系统、因果稳定数字滤波器的设计、倒谱和倒滤波的计算和处理等。在现有“数字信号处理”课程教学环节中，主要集中于对最小相位系统本身定义及特性的抽象阐述，相关的教学案例和素材也极少。

为更深刻地了解最小相位系统特性及工作机理，本文利用Matlab中FDATool工具设计IIR滤波器和与之对应的最小相位系统，通过对比信号经过两个系统的时域波形变化，对最小相位系统的重要性质进行验证，以助学生对最小相位系统的理解。

1 最小相位系统定义与性质

1.1 定义

零极点都在z平面单位圆内的系统，称为最小相位系统，记作Hmin;类似地，零点有在z平面单位圆内也有在单位圆外的因果稳定系统，称为混合相位系统，记作H;零点全在z平面单位圆外的因果稳定系统，称为最大相位系统，记作Hmax。

从定义来看，最小相位系统一定是因果稳定系统。最小相位系统的冲激响应h(t)称为最小相位序列。

1.2 性质

［性质1] 在具有相同幅频特性的因果稳定系统中，最小相位系统具有最小的相位延时。

我们通过对二阶最小相位系统Hmin、同幅频特性的混合相位系统H和同幅频特性的最大相位系统Hmax的相位进行比较(如图1所示)，可以发现最小相位系统有负的相位，但相位绝对值最小。其中Hmin(z)，H(z)和Hmax(z)表达式如下:

其中，系统的幅频特性主要受零极点分布的影响，而与系统函数的增益K无关。当两因果稳定系统具有相同零极点分布，增益满足线性比例关系时，它们与同阶Hmin(z)相位相比可以得到类似结论。

图1 H、Hmin和Hmax相位比较图

［性质2]任一实系数因果稳定系统H(z)都可表示为一个最小相位系统和一个全通系统的级联，即H(z)=Hmin(z)Am(z)。

证明:设系统H(z)只有一个零点z=1/a*在单位圆外，|a|＜1，那么该H(z)就可以表示成H(z)=H1(z)(z-1－a*)。根据定义，H1(z)是一个最小相位系统。

H(z)也可等效的表示为

由此可得，H(z)=Hmin(z)A1(z)。以此类推可以得到H(z)=Hmin(z)Am(z)。证毕。

Am(z)是全通系统，满足系统幅度响应恒为常数，故H(z)和Hmin(z)必然满足相同的幅度响应。

［性质3] 在幅频特性|H(ejω)|相同的系统中，最小相位系统具有最小的群延时。

［性质4] 在幅频特性|H(ejω)|相同的系统中，存在唯一的最小相位系统。

［性质5] 对具有相同傅里叶变换幅度的各序列，最小相位序列的hmin(0)最大。

性质3、4、5可由性质1得到，推导过程参见文献［1] 。

2 IIR滤波器设计与实现

我们采用Matlab工具设计实现最小相位系统并验证相关性质。根据性质2，考虑设计一个实系数因果稳定IIR滤波器(系统)，并找到其对应最小相位系统和全通系统的级联形式。由于IIR滤波器和最小相位系统均为非线性相位系统，信号经过这两种系统后时域波形会发生滞后平移。通过比较输出时域波形的滞后平移程度，验证最小相位系统的相关性质。IIR滤波器的经典设计方法是设计满足技术指标的模拟滤波器，利用脉冲响应不变法或双线性变换法，将模拟滤波器转换为数字滤波器［2]。然而，经典设计方法仅限于几种标准的低通、高通、带通和带阻滤波器设计，比如Butterworth滤波器、切比雪夫I/II型滤波器和椭圆滤波器等，对具有任意形状或者多频带滤波器的设计则无能为力［3]。IIR滤波器的直接设计方法是利用Matlab的Yulewalk函数［3]，使用最小二乘法拟合给定频率，使设计的滤波器达到期望频率特性。

在本实验中，采用Matlab中FDATool工具来设计并实现IIR滤波器，并找到相应最小相位系统和全通系统的级联形式。具体可以采用如下方法:

(1)利用FDATool工具设计满足一定频率特性的IIR滤波器，如图2所示。

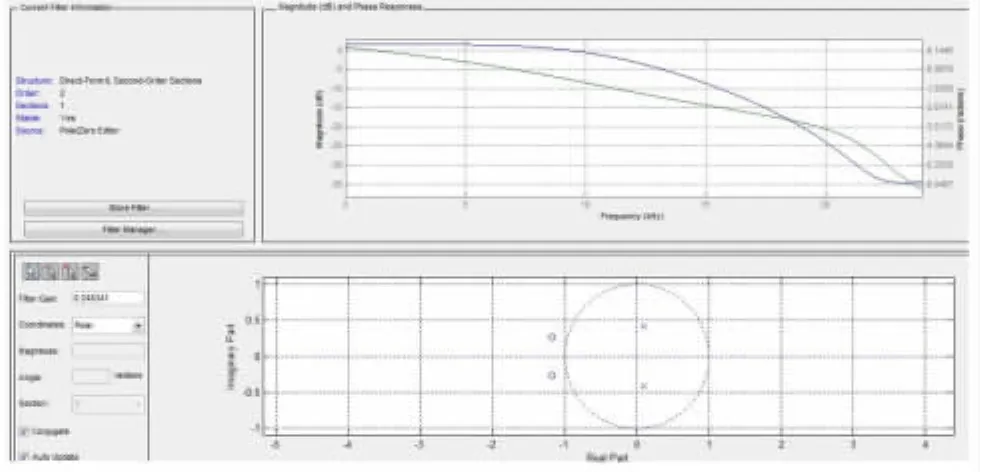
图2 利用FDATool工具设计IIR滤波器

(2)将IIR滤波器单位圆上零点拉出单位圆，得到零点全部在单位圆外的IIR滤波器。

(3)对调IIR系统函数H(z)二阶式表达中分子系数，即可得到二阶式表达的直接II型最小相位系统的系统函数:

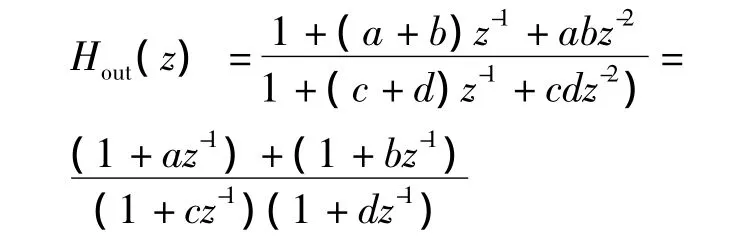
其中，|a|和|b|＞1，|c|和|d|＜1。Hout(z)是零点都在单位圆外的因果稳定系统，Hout(z)对应的最小相位系统可表示为

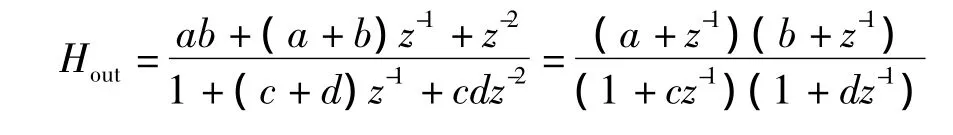
(4)通过IIR和最小相位系统两者系统函数相除，可以得到全通系统函数。

相比于经典和直接设计方法，利用FDATool工具设计并实现IIR滤波器更加直观和便捷。

3 实验验证步骤

1)设定输入信号—不失一般性选择两种不同频率的正弦信号叠加作为输入信号:

2)利用Matlab的FDATool工具设计IIR系统;

3)由IIR滤波器求得等幅度响应的最小相位系统—根据前述介绍，设计得到IIR滤波器、最小相位系统和全通系统，相应系统函数分别表示为

三个系统的零极点分布如图3所示。图中o和x分别表示零点和极点。图3(b)所示的最小相位系统的零极点都在z平面单位圆内，且与图3(a)所示的IIR系统的零点成倒数关系，极点相同。图3(c)所示的全通系统的零极点存在共轭倒数的关系，即p=(1/z)。而且，全通系统的零点和IIR系统零点相同，极点位置是最小相位系统零点的位置。

图3 H(z)、Hmin(z)和Am(z)零极点分布

三个系统的频率响应如图4所示。对比图4(a)所示IIR系统和图4(b)的最小相位系统，它们具有相同的幅度响应。图4(c)所示的全通系统幅度响应恒为常数，即0dB。由图4的相位响应曲线可见:最小相位系统具有最小的相位延时。

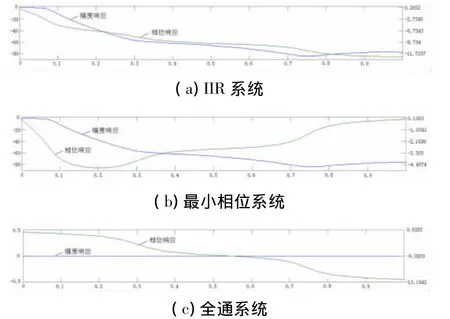
图4 H(z)、Hmin(z)和Am(z)频率响应

4)比较输入信号经过IIR滤波器和最小相位系统的输出信号时域波形—输入信号采样频率为100kHz，低通滤波器截止频率为12kHz。如图5所示，输入信号通过IIR系统和最小相位系统后，输出信号的时域波形发生变化，这主要是由于两个系统相位非线性变化导致高频分量被滤除所引起的。特别地，相比于最小相位系统，输入信号通过IIR系统后的时域波形平移明显，说明最小相位系统具有最小的相位延迟。

4 结语

本文阐述了最小相位系统的含义和性质并利用Matlab中FDATool工具设计最小相位系统。

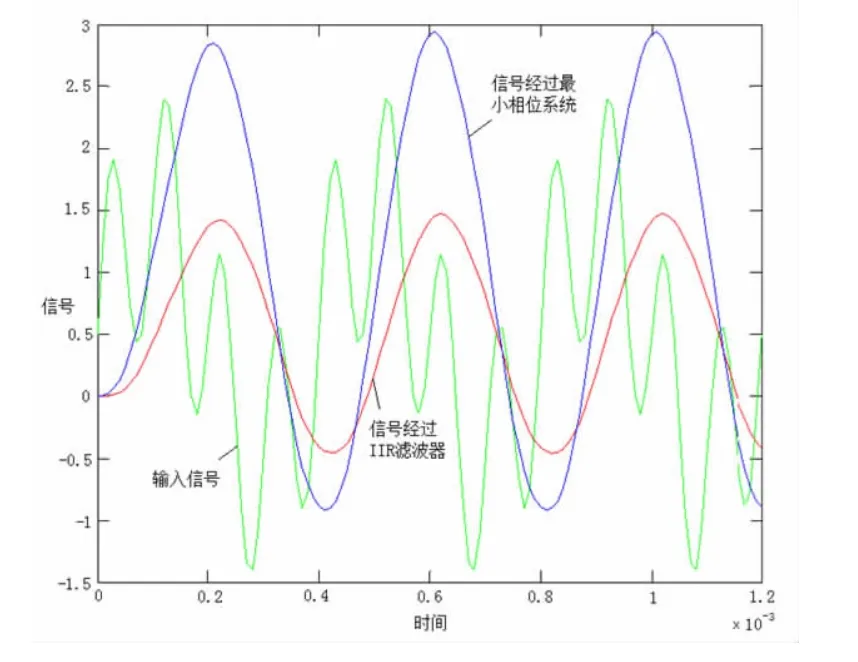
图5 通过IR滤波器和最小相位系统后的时域波形对比

本文所述的实验环节验证了最小相位系统的几个重要性质。笔者的“数字信号处理”课程教学实践证明:该教学案例有助于学生对最小相位系统的原理、设计及实现形成清楚和直观的认知。

［1] 程佩青.《数字信号处理教程》第二版［M] .北京:清华大学出版社.2007.2

［2] 陈后金，薛健，胡健.《数字信号处理》第二版［M] .北京:高等教育出版社.2008.11

［3] 胡晓东，董辰辉.《MATLAB从入门到精通》［M] .北京:人民邮电出版社.2010.6