DFT Study on the Electronic and Structural Properties of MoS6-/0 Clusters①

WU Ni ZHANG Chng-Fu ZHOU Qi HUANG Xin, ZHANG Yong-Fn, DING Ki-Ning WANG Bin, ② (Deprtment of Chemistry, Fuzhou University, Fuzhou 350108, Chin) (Fujin Provincil Key Lortory of Theoreticl nd Computtionl Chemistry, Ximen 361005, Chin)

1 INTRODUCTION

It is well known that molybdenum sulfide has intensely caught people's eyes due to their wide applications in solid lubricant, hydrogen storage,solar water splitting cells, petroleum refining catalyst and so on[1-5]. In particular, molybdenum disulfide and related compounds, generally termed MoSx, as catalysts are promising candidates in hydrogen evolution reaction (HER)[6-8]and hydrodesulfurization (HDS)[9-10]. But up to now, the underlying catalytic mechanisms and the identification of catalytic active sites are still unclear yet although they have been used for several decades. Recently,Topsøe et al.[10]put forward the special brim sites and edge in MoS2which performs a significant function in the steps of hydrodesulfurization (HDS).Merki et al. showed that the catalytically active species appeared to be reduced molybdenum sulfide that contains disulfide ligands[7]. Despite the considerable progress having been achieved, more detailed studies on the activity of molybdenum sulfide catalysts are required.

As known to all, gas-phase clusters are able to be used as effective models to obtain mechanistic understanding of the sophisticated surface structures and catalytic processes at a molecular level[11-14]. It is our point of interest in probing the electronic and structural properties of mononuclear molybdenum sulfide clusters and their anions, aiming at providing well-defined molecular models for bulk surfaces and catalysts. There have been relatively few studies with respect to the mono-molybdenum sulfide clusters[15-17]. Therein, Gemming et al. presented the photoelectron spectra and theoretical studies involving electronic and geometric structures of the MxSy(M = Mo, W; x = 1-4) clusters[15,18]. In their study[15], a behavior of sequential sulfidation was observed for MoSx(x = 1-6). And the MoS6-/0clusters were predicted to be the structures with two side-on S3units[15]. But they did not offer the experimental spectra because of the difficulty of unambiguous mass separation. And we surmised more flexible sulfur ligands may be found for the ground state of MoS6-/0. In addition, the simulated photoelectron spectra can be served as the complement to the experiment, which can be also used as the fingerprint to distinguish the clusters detected.

In our present work, extensive density functional theory (DFT) calculations combined with photoelectron spectra (PES) were performed to elucidate the electronic structures and chemical bonding in the mononuclear molybdenum sulfide clusters, MoS6-/0.According to our calculations, diverse sulfur ligands(i.e., terminal S2-, polysulfide S22-and S32-units) are found in neutral MoS6(Cs,1A'). And disparate geometric structures are located for MoS6-/0when compared with the previous study[15]. It is worth mentioning that the polysulfide (Sx, x ≥ 2) units emerge in molybdenum sulfide clusters, which may play an important role in studying the activity of the catalyst[19-22].

2 COMPUTATIONAL METHODS

Density functional theory (DFT) calculations employing the B3LYP hybrid functional[23-25]were carried out using Gaussian 03 program[26]. A host of structural candidates including different spin states and initial geometries were evaluated, and the search for global minima was first performed using the triple-ζ valence plus polarization (def2-TZVP) basis set[27-29]and the corresponding effective core potential for Mo[30]within the Gaussian 03 program.Selected low-lying isomers (≤ 0.3 eV) were further reoptimized at the B3LYP hybrid functional, using the Stuttgart relativistic small core basis set and efficient core potential[31]augmented with two f-type and one g-type polarization functions (ζ(f) = 0.338,1.223; ζ(g) = 0.744) for molybdenum as recommended by Martin and Sundermann[32]and the aug-cc-pvtz basis set for sulfur[33]. Vibrational frequency calculations were performed at the same level of theory to verify the nature of the stationary points. And in our previous studies, B3LYP gave superior results in terms of energies when directly compared to the experimental results. As discussed below, we used the results with B3LYP functional for further discussion. The relative stabilities of low-lying structures (ΔE ≤ 0.3 eV) were further evaluated via single point CCSD(T)[34-38]calculations with the Mo/Stuttgart+2f1g/S/aug-cc-pvtz basis sets at the B3LYP geometries. The CCSD(T)calculations were performed using the MOLPRO 2010.1 package[39].

Vertical electron detachment energies (VDEs)were calculated using the generalized Koopmans’theorem by adding a correction term to the eigenvalues of the anion[40]. The correction term was calculated as δE = E1- E2- εHOMO, where E1and E2are the total energies of the anion and neutral,respectively in their ground states at the anion equilibrium geometry and εHOMOcorresponds to the eigenvalue of the highest occupied molecular orbital(HOMO) of the anion. All calculations were performed with the Gaussian 03 software package.

3 THEORETICAL RESULTS AND DISCUSSION

The optimized ground-state structures and selected low-lying isomers of MoS6-/0at the B3LYP/Mo/Stuttgart+2f1g/S/aug-cc-pvtz level of theory are presented in Figs. 1 and 2, respectively. And the results of CCSD(T) single-point calculations for the low-lying isomers (≤ 0.3 eV) are listed in Table 1.The calculated ADEs (adiabatic detachment energies)and VDEs for the global minima and selected low-lying isomers (ΔE ≤ 0.3 eV) are presented in Table 2. The simulated PES from the ground state and selected isomers (≤ 0.3 eV) are shown in Fig.3. Alternative optimized structures of MoS6-/0along with their relative energies at the B3LYP/Mo/def2-TZVP/S/def2-TZVP level are collected in the Supporting Infor- mation (Fig. S1-S2).

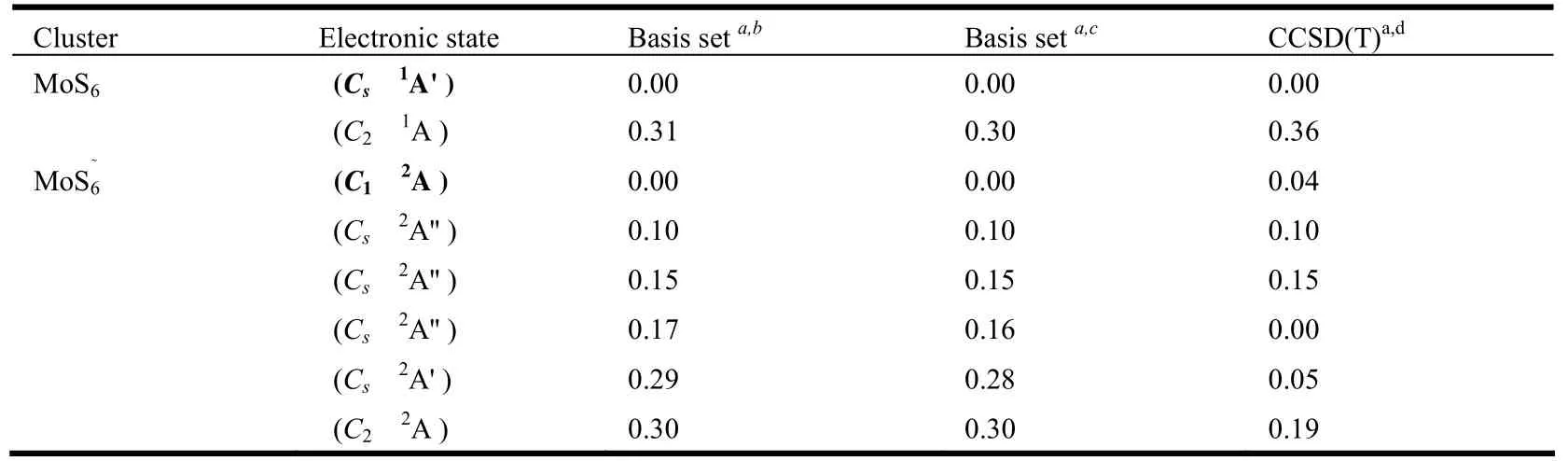
Table 1. Relative Energies of the Low-lying States of the MoS6-/0 Clusters at the B3LYP Level (≤ 0.3 eV), and Comparisons with Those from the CCSD(T) Single Point Calculations at the B3LYP Geometries (≤ 0.3 eV)

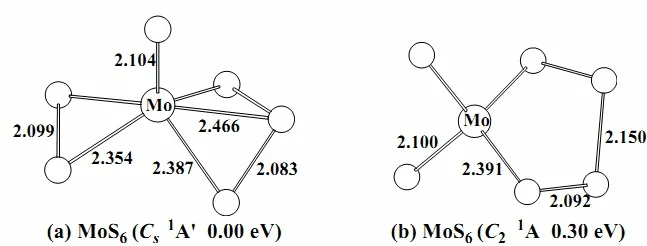
Fig. 1. Optimized structures for MoS6 at the B3LYP level of theory. Selected bond distances (Å) are shown

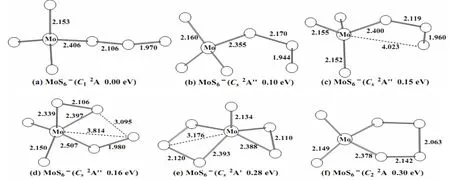
Fig. 2. Optimized structures for MoS6- at the B3LYP level of theory. Selected bond distances (Å) are shown

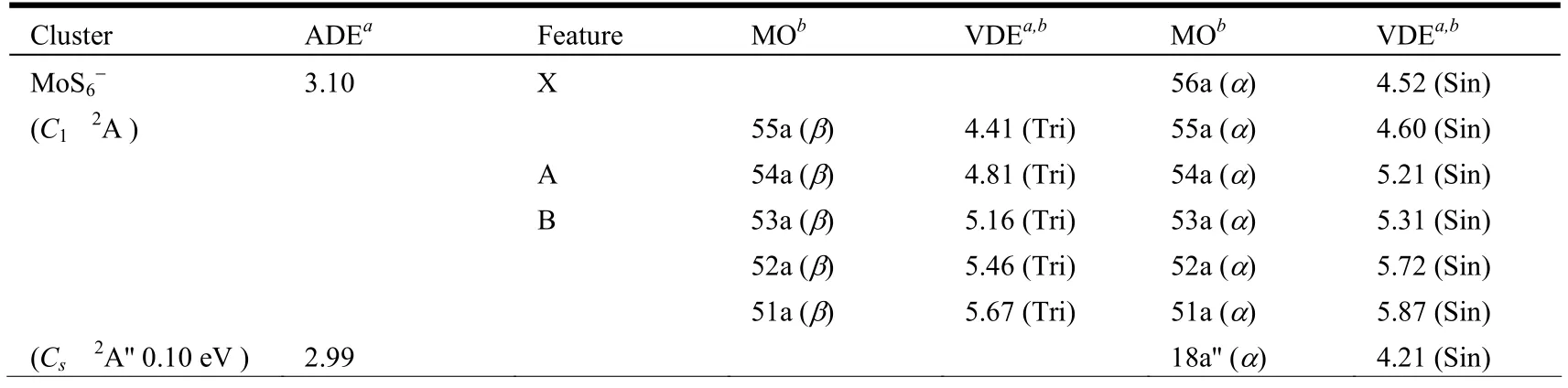
Table 2. Theoretical Adiabatic Detachment Energies (ADEs) and Vertical Detachment Energies (VDEs) of theLowest-energy MoS6- Cluster and the Selected Low-lying Isomers at the B3LYP/Mo/Stuttgart+2f1g/S/aug-cc-pvtz Level of Theory

To be continued

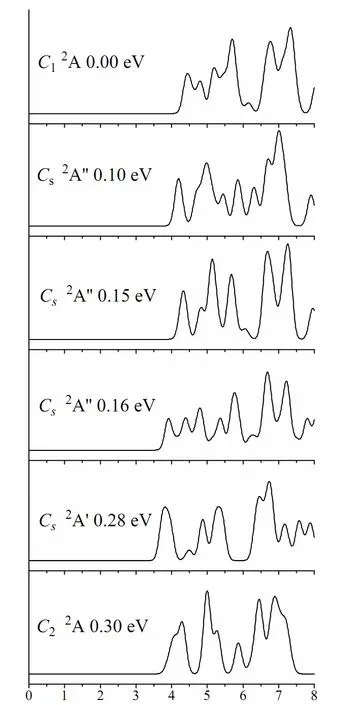
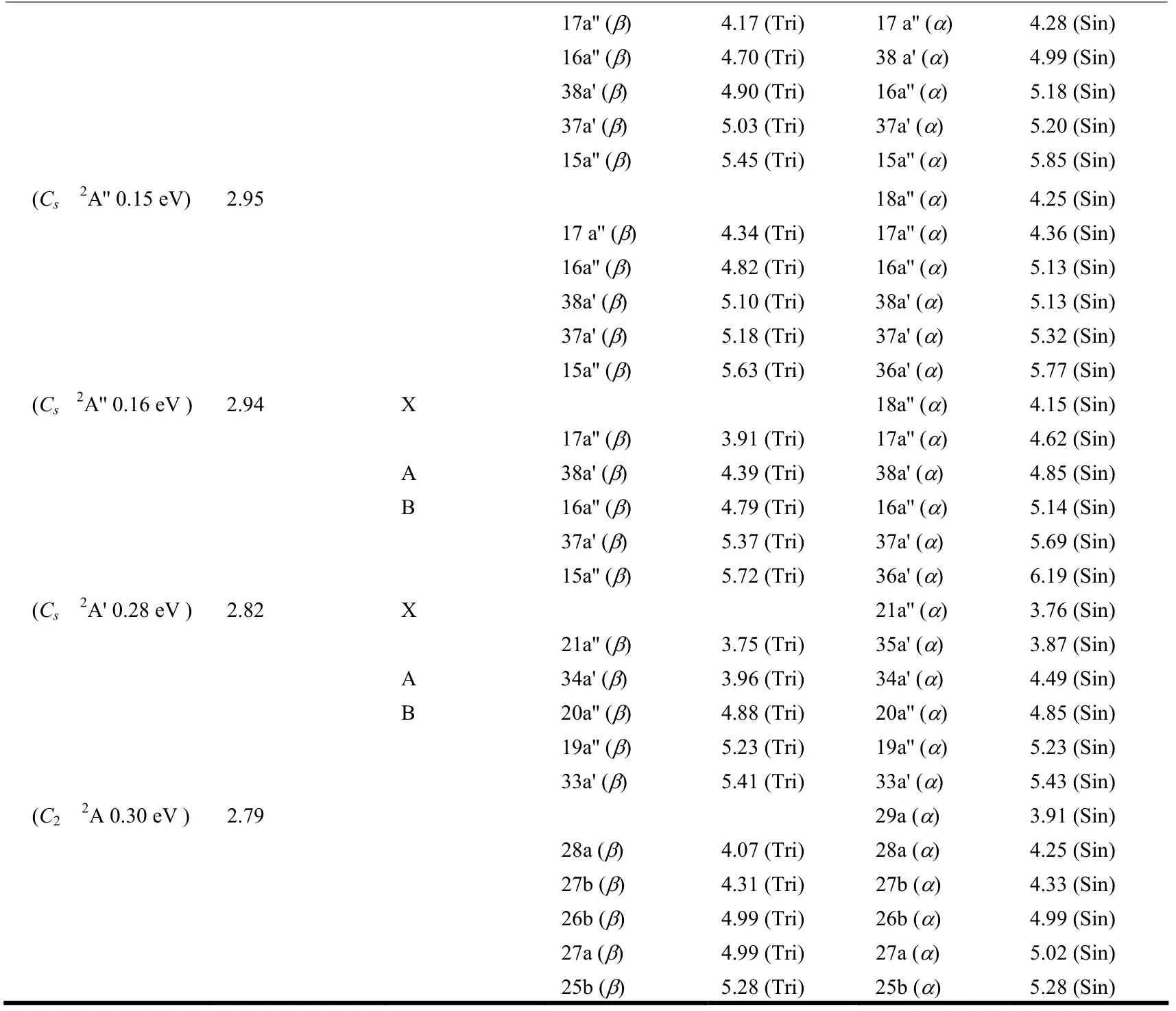
Fig. 3. Simulated photoelectron spectra of MoS6- from ground state and selected low-lying isomers.The simulations are done by fitting the distribution of calculated VDEs with unit-area Gaussian functions of 0.1 eV width

3.1 Optimized results: MoS6-/0 clusters

The ground state of MoS6is predicted to be closed-shell (Cs,1A') with a terminal S atom, a side-on S2group and a side-on S3group (Fig. 1a).Another singlet (C2,1A) isomer in which the molybdenum is coordinated with two terminal S atoms and a S4ligand is 0.30 eV higher in energy (Fig. 1b).Single-point CCSD(T) calculations were carried out for these two isomers. And the CCSD(T) results show that the (Cs,1A') isomer (Fig. 1a) is the lowestenergy structure.

By contrast, the potential energy surface for MoS6-is much more flat. There are several closely lying isomers near the global minimum. An openshell (C1,2A) structure (Fig. 2a) with one end-on S3unit is predicted to be the lowest-energy anion. The bond length between the Mo atom and the nearest S atom in S3unit is 2.406 Å. And two isomers (Fig. 2b and 2c) with similar skeleton are located, both of which are slightly higher in energy (0.10 and 0.15 eV, respectively). Another doublet state (Cs,2A'')with two terminal S atoms, a side-on S2unit and an end-on S2unit, is found to be 0.16 eV higher in energy (Fig. 2d). And the isomer (Cs,2A'), which is similar with the neutral ground state, is 0.28 eV higher in energy (Fig. 2e). The isomer (C2,2A) with a S4ligand (Fig. 2f) is also located to be 0.30 eV higher. All these low-lying isomers are further evaluated via CCSD(T) single-point calculations at the B3LYP geometries. As shown in Table 1, the (Cs,2A'') isomer (Fig. 2d) is located at the ground state.But the (C1,2A) (Fig. 2a) and (Cs,2A') (Fig. 2e)isomers are only 0.04 and 0.05 eV higher in energy,respectively. More sophisticated methods, such as full CCSD(T) structural optimization, may be valuable to further resolve the true ground state of MoS6-.

It is worth mentioning that, in the previous study[15], the structures with two S3units were predicted to be the ground states of MoS6-/0. These geometries are also taken into our consideration, but they are much higher in energy (2.09 eV for anion and 1.38 eV for neutral, see Supporting Information).As mentioned above, the ground state of MoS6is predicted to be closed-shell (Cs,1A') with a terminal S atom, a side-on S2group and a side-on S3group.In this structure, the molybdenum reaches its highest oxidation state +6. While in the structure with two S3units, the oxidation state of Mo is +4. In other words, the Mo atom prefers its highest oxidation state in the sulfur-rich MoS6-/0clusters. Hence, we considered the structure (Fig. 1a) to be the neutral MoS6ground state. And there is a competition between terminal S and polysulfide ligands in the anionic MoS6-cluster. These energy-degenerate isomers compete for the anionic ground state.

3.2 Interpretation of the simulated photoelectron spectra and molecular orbital analyses

The vertical detachment energies (VDEs) of MoS6-were calculated on the basis of the ground state and selected low-lying isomers (ΔE ≤ 0.3 eV)by means of the generalized Koopmans’ theorem(Table 2). And the simulated PES for the global minima and selected low-lying isomers (ΔE ≤ 0.3 eV) are shown in Fig. 3. As follows, we will attempt to qualitatively account for the simulated PES features using molecular orbital analyses. Considering the complicated nature of the electronic structure of MoS6-, some assignments should be considered tentatively.

The frontier orbitals of MoS6and MoS6-are illustrated in Figs. 4–7. For the neutral species, the MoS6(Cs,1A') structure (Fig. 1a) with one terminal S, one S2and one S3is shown to be the ground state utilizing both DFT and CCSD(T) single-point calculations. The HOMO (21a'')2and HOMO-4(19a'')2(Fig. 4) correspond to the two π* orbitals of the bound S2unit in MoS6(Cs,1A'). It is interesting to note that the bond length of S–S in S2moiety is 2.099 Å (Fig. 1a), which is very similar to that of free persulfide S22-anion (2.180 Å calculated at the same level). Thus, we can consider these two orbitals are fully occupied in the free S22-.anion.And the HOMO-2 (34a')2and HOMO-3 (33a')2contain two π* orbitals of the contacted S3group in MoS6(Cs,1A'). Intriguingly, we found that the S–S bond length is 2.083 Å and the ∠S–S–S angle 104.75º, which are similar with those in the trisulfide S32-anion (2.134 Å and 113.97º calculated at the same level). Hence, we figure out that these two orbitals are fully occupied in the free S32-anion.Consequently, as for the lowest-energy structure of the neutral species, the molybdenum is coordinated with a terminal S2-, a persulfide S22-and a trisulfide S32-ligand. And the Mo atom reaches its highest oxidation state of +6.

Fig. 4. Frontier molecular orbitals for the neutral MoS6 ground state (Fig. 1a)

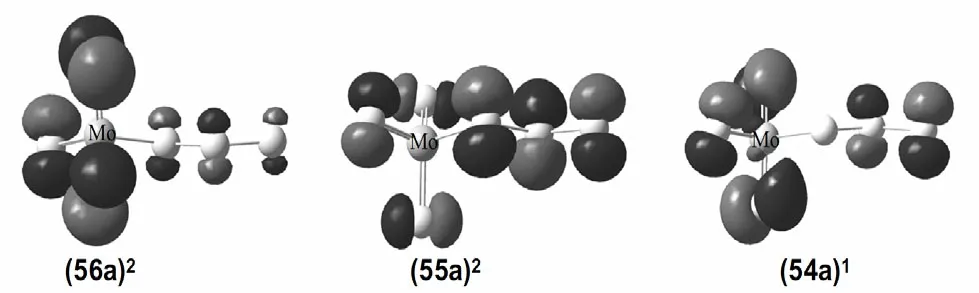
Fig. 5. Frontier molecular orbitals of MoS6- (Fig. 2a)

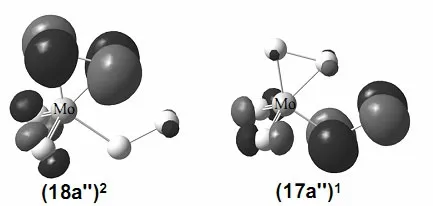
Fig. 6. Frontier molecular orbitals of MoS6- (Fig. 2d)

Fig. 7. Frontier molecular orbitals of MoS6- (Fig. 2e)

As for the anion, three isomers (Fig. 2a, 2d and 2e)are nearly degenerated via CCSD(T) single-point calculations. For the (C1,2A) isomer (Fig. 2a), it has a valence electron configuration of ·· (54a)1(55a)2(56a)2(Fig. 5). Photodetachment from the doubly occupied orbital (56a)2yields the X band with the calculated VDEs of 4.41 eV (β) and 4.52 eV (α), respectively.The (Cs,2A'') isomer (Fig. 2d) has a valence electron configuration of ·· (38a')2(17a'')1(18a'')2. The doubly occupied (18a'')2is primarily a S–S π-antibonding orbital (Fig. 6). Photodetachment from this orbital yields the X band with the calculated VDEs of 3.91 eV (β) and 4.15 eV (α), respectively. And the (Cs,2A') (Fig. 2e) has a valence electron configuration of ·· (34a')1(35a')2(21a'')2(Fig. 7). Photodetachment from the doubly occupied (21a'')2yields the X band with the calculated VDEs of 3.75 eV (β) and 3.89 eV (α), respectively.

3.3 Polysulfide ligands in MoS6-/0 clusters

It is reported that polysulfides (Sx2-, x ≥ 2) can bridge two or more metal atoms in different patterns[41-42], resulting in a variety of structures. Previous studies[19-20]showed that polysulfide reductase can catalyze the reduction of polysulfide Sn2-to S(n-1)2-(Eq. 1). Recently, Afanasiev et al. delivered that the S22-species located at the edges of fresh MoS2catalysts play a key part for the catalytic activity[21-22].

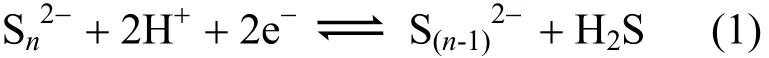
In our calculations, diverse sulfur ligands (i.e.,terminal S2-, polysulfide S22-and S32-units) emerge in the MoS6cluster. Further progress in such studies may provide more insight into the development of modified catalyst.

4 CONCLUSION

We report a comprehensive investigation of the electronic structure and chemical bonding in MoS6-/0using density functional theory calculations. Vertical electron detachment energies (VDEs) are calculated using the generalized Koopmans’ theorem by adding a correction term to the eigenvalues of the anions.Molecular orbitals are used to analyze the chemical bonding in MoS6-. In light of our calculations, the terminal S2-, polysulfide S22-and S32-ligands simultaneously emerge in the neutral MoS6cluster.Various polysulfide units are also found in the anionic MoS6-cluster.

(1) Rapoport, L.; Moshkovich, A.; Perfilyev, V.; Laikhtman, A.; Lapsker, I.; Yadgarov, L.; Rosentsveig, R.; Tenne, R. High lubricity of Re-doped lullerene-like MoS2nanoparticles. Tribol. Lett. 2012, 45, 257-264.

(2) Ye, L. N.; Wu, C. Z.; Guo, W.; Xie, Y. MoS2hierarchical hollow cubic cages assembled by bilayers: one-step synthesis and their electrochemical hydrogen storage properties. Chem. Commun. 2006, 45, 4738-4740.

(3) Chen, J.; Kuriyama, N.; Yuan, H.; Takeshita, H. T.; Sakai, T. Electrochemical hydrogen storage in MoS2nanotubes.J. Am. Chem. Soc. 2001, 123, 11813-11814.

(4) Walter, M. G.; Warren, E. L.; McKone, J. R.; Boettcher, S. W.; Mi, Q.; Santori, E. A.; Lewis, N. S. Solar water splitting cells.Chem. Rev. 2010, 110, 6446-6473.

(5) Kisielowski, C.; Ramasse, Q. M.; Hansen, L. P.; Brorson, M.; Carlsson, A.; Molenbroek, A. M.; Topsøe, H.; Helveg, S. Imaging MoS2nanocatalysts with single-atom sensitivity. Angew. Chem. Int. Ed. 2010, 49, 2708-2710.

(6) Laursen, A. B.; Kegnæs, S.; Dahl, S.; Chorkendorff, I. Molybdenum sulfides efficient and viable materials for electro- and photoelectrocatalytic hydrogen evolution. Energy Environ. Sci. 2012, 5, 5577-5591.

(7) Vrubel, H.; Merki, D.; Hu, X. L. Hydrogen evolution catalyzed by MoS3and MoS2particles. Energy Environ. Sci. 2012, 5, 6136-6144.

(8) Lau, V. W. H.; Masters, A. F.; Bond, A. M.; Maschmeyer, T. Ionic-liquid-mediated active-site control of MoS2for the electrocatalytic hydrogen evolution reaction. Chem. Eur. J. 2012, 18, 8230-8239.

(9) Moses, P. G.; Hinnemann, B.; Topsøe, H.; Nørskov, J. K. The effect of Co-promotion on MoS2catalysts for hydrodesulfurization of thiophene: a density functional study. J. Catal. 2009, 268, 201-208.

(10) Besenbacher, F.; Brorson, M.; Clausen, B. S.; Helveg, S.; Hinnemann, B.; Kibsgaard, J.; Lauritsen, J. V.; Moses, J. K.; Topsøe, H. Recent STM,DFT and HAADF-STEM studies of sulfide-based hydrotreating catalysts: insight into mechanistic, structural and particle size effects. Catal. Today 2008, 130, 86-96.

(11) Johnson, G. E.; Tyo, E. C.; Castleman, A. W. Jr. Cluster reactivity experiments: employing mass spectrometry to investigate the molecular level details of catalytic oxidation reactions. PNAS 2008, 105, 18108-18113.

(12) Waters, T.; Huang, X.; Wang, X. B.; Woo, H. K.; O’Hair, R. A. J.; Wedd, A. G.; Wang, L. S. Photoelectron spectroscopy of free multiply charged keggin anions α-[PM12O40]3-(M = Mo, W) in the gas phase. J. Phys. Chem. A 2006, 110, 10737-10741.

(13) Böhme, D. K.; Schwarz, H. Gas-phase catalysis by atomic and cluster metal ions: the ultimate single-site catalysts. Angew. Chem., Int. Ed. 2005, 44,2336-2354.

(14) Castleman, A. W. Jr. Cluster structure and reactions: gaining insights into catalytic processes. Catal. Lett. 2011, 141,1243–1253.

(15) Gemming, S.; Tamuliene, J.; Seifert, G.; Bertram, N.; Kim, Y. D.; Ganteför, G. Electronic and geometric structures of MoxSyand WxSy(x = 1, 2, 4; y= 1–12) clusters. Appl. Phys. A 2006, 82, 161-166.

(16) Liang, B.; Andrews, L. Infrared spectra and density functional theory calculations of group 6 transition metal sulfides in solid Argon. J. Phys. Chem.A 2002, 106, 6945-6951.

(17) Murugan, P.; Kumar, V; Kawazoe, Y; Ota, N. Ab initio study of structural stability of Mo-S clusters and size specific stoichiometries of magic clusters. J. Phys. Chem. A 2007, 111, 2778-2782.

(18) Gemming, S.; Seifert, G.; Götz, M.; Fischer, T.; Ganteför, G. Transition metal sulfide clusters below the cluster-platelet transition: theory and experiment. Phys. Status Solidi B 2010, 247, 1069-1076.

(19) Hille, R. Molybdenum enzymes containing the pyrano-pterin cofactor: an overview, Marcel Dekker, Inc., New York 2002.

(20) Enemark, J. H.; Cooney, J. J. A.; Wang, J. J.; Holm, R. H. Synthetic analogues and reaction systems relevant to the molybdenum and tungsten oxotransferases. Chem. Rev. 2004, 104, 1175-1200.

(21) Afanasiev, P. The influence of reducing and sulfiding conditions on the properties of unsupported MoS2-based catalysts.J. Catal. 2010, 269, 269-280.

(22) Afanasiev, P.; Jobic, H.; Lorentz, C.; Leverd, P.; Mastubayashi, N.; Piccolo, L.; Vrinat, M. Low-temperature hydrogen interaction with amorphous molybdenum sulfides MoSx. J. Phys. Chem. C 2009, 113, 4139-4146.

(23) Becke, A. D. A new mixing of Hartree-Fock and local density-functional theories. J. Chem. Phys. 1993, 98, 1372-1377.

(24) Lee, C.; Yang, W.; Parr, R. G. Development of the colic-salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785-789.

(25) Stephens, P. J.; Devlin, F. J.; Chabalowski, C. F.; Frisch, M. J. Ab initio calculation of vibrational absorption and circular dichroism spectra using density functional force fields. J. Phys. Chem. 1994, 98, 11623-11627.

(26) Frisch, M. J.; Trucks, G. W.; Schlegel, H. B.; Scuseria, G. E.; Robb, M. A.; Cheeseman, J. R.; Montgomery, J. A. Jr.; Vreven, T.; Kudin, K. N.;Burant, J. C.; Millam, J. M.; Iyengar, S. S.; Tomasi, J.; Barone, V.; Mennucci, B.; Cossi, M.; Scalmani, G.; Rega, N.; Petersson, G. A.; Nakatsuji, H.;Hada, M.; Ehara, M.; Toyota, K.; Fukuda, R.; Hasegawa, J.; Ishida, M.; Nakajima, T.; Honda, Y.; Kitao, O.; Nakai, H.; Klene, M.; Li, X.; Knox, J. E.;Hratchian, H. P.; Cross, J. B.; Bakken, V.; Adamo, C.; Jaramillo, J.; Gomperts, R.; Stratmann, R. E.; Yazyev, O.; Austin, A. J.; Cammi, R.; Pomelli,C.; Ochterski, J. W.; Ayala, P. Y.; Morokuma, K.; Voth, G. A.; Salvador, P.; Dannenberg, J. J.; Zakrzewski, V. G.; Dapprich, S.; Daniels, A. D.;Strain, M. C.; Farkas, O.; Malick, D. K.; Rabuck, A. D.; Raghavachari, K.; Foresman, J. B.; Ortiz, J. V.; Cui, Q.; Baboul, A. G.; Clifford, S.;Cioslowski, J.; Stefanov, B. B.; Liu, G.; Liashenko, A.; Piskorz, P.; Komaromi, I.; Martin, R. L.; Fox, D. J.; Keith, T.; Al-Laham, M. A.; Peng, C. Y.;Nanayakkara, A.; Challacombe, M.; Gill, P. M. W.; Johnson, B.; Chen, W.; Wong, M. W.; Gonzalez, C. Pople, J. A. Gaussian 03; Revision D. 01;Gaussian, Inc.: Wallingford, CT 2004.

(27) Schäfer, A.; Huber, C.; Ahlrichs, R. Fully optimized contracted gaussian basis sets of triple zeta valence quality for atoms Li to Kr. J. Chem. Phys.1994, 100, 5829–5835.

(28) Weigend, F.; Ahlrichs, R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305.

(29) Eichkorn, K.; Weigend, F.; Treutler, O.; Ahlrichs, R. Auxiliary basis sets for main row atoms and transition metals and their use to approximate Coulomb potentials. Theor. Chem. Acc. 1997, 97, 119-124. The exponents (included those of the polarization functions) and contraction coefficients can be retrieved from the following website: https://bse.pnl.gov/bse/portal.

(30) Andrae, D.; Häußermann, U.; Dolg, M.; Stoll, H.; Preuß, H. Energy-adjusted ab initio pseudopotentials for the second and third row transition elements. Theor. Chem. Acc. 1990, 77, 123–141.

(31) Küchle, W.; Dolg, M.; Stoll, H.; Preuss, H. Pseudopotentials of the Stuttgart/Dresden group 1998, revision August 11 1998;http://www.theochem.uni-stuttgart.de/pseudopotentiale.

(32) Martin, J. M. L.; Sundermann, A. Correlation consistent valence basis sets for use with the Stuttgart-Dresden-Bonn relativistic effective core potentials: the atoms Ga-Kr and In-Xe. J. Chem. Phys. 2001, 114, 3408-3420.

(33) Woon, D. E.; Dunning, T. H. Jr. Gaussian basis sets for use in correlated molecular calculations. III. the atoms aluminum through argon. J. Chem.Phys. 1993, 98, 1358-1371.

(34) Purvis, G. D. III; Bartlett, R. J. A full coupled-cluster singles and doubles model: the inclusion of disconnected triples. J. Chem. Phys. 1982, 76,1910-1918.

(35) Scuseria, G. E.; Janssen, C. L.; Schaefer, H. F. III. An efficient reformulation of the closed shell coupled cluster single and double excitation (CCSD)equations. J. Chem. Phys. 1988, 89, 7382-7387.

(36) Raghavachari, K.; Trucks, G. W.; Pople, J. A.; Head-Gordon, M. A fifth-order perturbation comparison of electron correlation theories. Chem. Phys.Lett. 1989, 157, 479-483.

(37) Watts, J. D.; Gauss, J.; Bartlett, R. J. Coupled-cluster methods with non-iterative triple excitations for restricted open-shell hartree-fock and other general single-determinant reference functions. energies and analytical gradients. J. Chem. Phys. 1993, 98, 8718-8733.

(38) Bartlett, R. J.; Musial, M. Coupled-cluster theory in quantum chemistry. Rev. Mod. Phys. 2007, 79, 291-352.

(39) Werner, H. J.; Knowles, P. J.; Manby, F. R.; Schütz, M.; Celani, P.; Knizia, G.; Korona, T.; Lindh, R.; Mitrushenkov, A.; Rauhut, G.; Adler, T. B.;Amos, R. D.; Bernhardsson, A.; Berning, A.; Cooper, D. L.; Deegan, M. J. O.; Dobbyn, A. J.; Eckert, F.; Goll, E.; Hampel, C.; Hesselmann, A.;Hetzer, G.; Hrenar, T.; Jansen, G.; Köppl, C.; Liu, Y.; Lloyd, A. W.; Mata, R. A.; May, A. J.; McNicholas, S. J.; Meyer, W.; Mura, M. E.; Nicklass,A.; O’Neill, D. P.; Palmieri, P.; Pflüger, K.; Pitzer, R.; Reiher, M.; Shiozaki, T.; Stoll, H.; Stone, A. J.; Tarroni, R.; Thorsteinsson, T.; Wang, M.;Wolf, A. MOLPRO, version 2010.1, a package of ab initio programs; see http://www.molpro.net.

(40) Tozer, D. J.; Handy, N. C. Improving virtual Kohn-Sham orbitals and eigenvalues: application to excitation energies and static polarisabilities. J.Chem. Phys. 1998, 109, 10180-10189.

(41) Matsumoto, K.; Matsumoto, T.; Kawano, M.; Ohnuki, H.; Shichi, Y.; Nishide, T.; Sato, T. Syntheses and crystal structures of disulfide-bridged binuclear ruthenium compounds: the first UV-Vis, raman, ESR, and XPS spectroscopic characterization of a valence-averaged mixed-valent RuIIISSRuICore. J. Am. Chem. Soc. 1996, 118, 3597-3609.

(42) Hossain, M. M.; Lin, Y. S.; Sugiyama, H.; Matsumoto, K. Allylic C-H bond activation on a sulfur center of a disulfide-bridged diruthenium complex with concomitant formation of C-S bonds. J. Am. Chem. Soc. 2000, 122, 172-173.