采用演化博弈的地质灾害人员疏散仿真

李蒙，丁凌灵，林从谋

（华侨大学 土木工程学院，福建 厦门361021）

近年来，人员疏散问题一直面临着严峻的挑战.尤其是当地质灾害发生时，一些场所由于人口稠密等原因导致疏散十分拥挤，一旦人群中发生拥挤践踏事件，后果十分严重.地质灾害的发生常常具有突发性，提前作出预测并及时采取有效、合理的人员疏散方案有其必要性.目前，针对人员疏散的研究可大体分为两类：一类是关于数学理论在人员疏散中的应用；另一类是利用元胞自动机（CA）来模拟人员疏散的过程.彭华等［1］利用平面解析几何知识为解决紧急疏散情况下的路径规划问题，提出一种新的算法；李俊［2］则介绍了国内外常用的疏散模型算法，并比较分析出最优的算法，利用仿真软件具体标定了算法中的参数，为建模及计算提供了参考；周金旺等［3］应用元胞自动机模拟了行人疏散的过程；宋伟等［4］用元胞自动机建立了人员的疏散模型；任书君等［5］则将元胞自动机与Agent技术相结合来研究人员的疏散过程；何大治等［6］从子空间网络方面建立了人员的疏散模型.以上方法虽对人员疏散过程进行了较好地描述或模拟，但都没有将人的行为因素考虑在疏散过程中，模拟结果可能存在较大的偏差.本文认为地质灾害中人员疏散也可看作一个演化博弈过程［7-8］.因此，提出一种基于演化博弈的地质灾害人员疏散仿真，结合演化博弈将人的行为因素补充到人员疏散的过程中.

1 人员疏散过程中的个体行为描述

假定在一个时间步长内，每个个体随机选择另一个个体，并观察其行为模式.当个体之间的行为模式相差不超过其观测距离时，个体之间的行为模式会发生变化.假设每个个体为一个智能体Agent，那么Agent之间的行为模式会按照一定的比例更接近对方，也有可能完全趋同.假设每个Agent在逃生的过程中，都会对逃生方向及方法持有自己的行为模式，令行为模式为I，I∈（0，1）.

若从人员中任意选择某两个个体Agent，他们各自的行为模式用Xi和Xj表示，其行为模式的观测距离为d，则当d＞｜Xi-Xj｜时，这两个个体才能够进行行为模式的交互.再假设行为模式之间的交互比例为p，两者进行交互后，各自的行为模式为

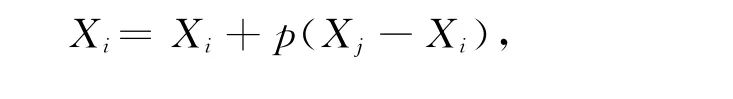
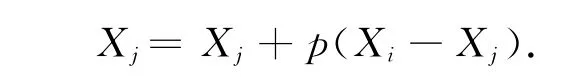
改变p值可以获得不同性质的群体.极端情况下，当p＝0时，参与交互的双方不发生行为模式的改变；当p＝1时，一方完全转变为另一方的行为模式.一般情况下，当p＝1／2时，是指交互双方均将发生一定的行为模式的改变，而改变值为其行为模式距离的算术平均值.

2 个体之间博弈模型的构建

地质灾害有多种，以山体滑坡为例，假设山体上已经出现滑坡趋势时，人群中会出现两类个体：A类和B类.每个个体都会对自己的行为模式（假定为是否逃生及逃生的路线和方法）持有自己的观点，A类个体I，I∈（0.5，1），B类个体I，I∈（0，1）.如果两类个体随机地一一配对，则可以构成了无数同质且独立的博弈单元.

若A类个体对于信息具有一定的优势，如年龄较大的个体有过躲避山体滑坡的经验，或受过一定的逃生培训，具有一定的逃生知识，或掌握正确及时资讯的个体，而B类个体则不具备此优势.当山体滑坡发生时，A类个体与A类个体进行配对，假定不会发生行为模式的交互，此时p＝0；而当A类个体与B类个体配对时，A类个体选择说服B类个体的概率为q，选择不说服的概率为1-q.B类个体也会采取相应的策略，那么B类个体选择相信的概率为i，选择不相信的概率为1-i.由于天气对灾害的发生会造成影响，天气良好，山体滑坡不发生的概率为j，山体滑坡如预期发生的概率为1-j.

当与选择说服策略的A类个体配对的B类个体，选择相信A类个体.若因天气良好，山体滑坡不发生，那么对于A类个体，除了得到固有收益之外，还可能会得到额外收益S（S＝1／d），同时A类个体也要付出说服成本C，则A类个体的总收益为R+S-C，而B类个体可能获得收益r，也可能因疏散造成家中无人而财物意外损失u，B类个体的总收益为r-u；若山体滑坡如预期发生，则B类个体有损失v（如房屋受损，但人身安全得到保障）.如果B类个体对A类个体的选择策略是不相信，对于A类个体，除了得到固有收益R之外，同样付出了说服成本C，则其收益是R-C；若因天气良好，山体滑坡不发生，则B类个体可能获得收益r，B类个体的总收益为r；若山体滑坡如预期发生，则B类个体有损失V.

当A类个体选择不说服的策略时，A类个体的收益仍然为R，如果B类个体选择盲目相信的策略，此时若跟着A类个体的疏散行为模式，若因天气良好，山体滑坡不发生，B类个体可能获得收益r［8］，也可能因疏散造成家中无人而财物意外损失u，B类个体的总收益为r-u；若山体滑坡如预期发生，则B类个体有损失V.但若是跟错了个体，跟着自己同类的个体则可能有被误导的可能性，从而造成一定的损失d，其中，d为两个随机选出个体之间的行为模式距离的绝对值.假设A类个体在疏散群体中所占的比例为k∈（0，1），而群体总数为n，则此时B类个体的收益期望值为r（k／n）-d（1-k）／n；如果B类个体选择不相信的策略，则A类个体的收益仍然为R，若因天气良好，山体滑坡不发生，则B类个体可能获得收益r，B类个体的总收益为r；若山体滑坡如预期发生，则B类个体有损失V.假设A类个体的可能获得收益与其付出成本成比例C＝x／d.

在上述假定的情况下，每个个体的收益不仅与自己的选择有关，也与和自己博弈的对方的选择有关，还与天气状况有关.分别计算每类个体的期望收益和平均收益.

A类个体的收益为

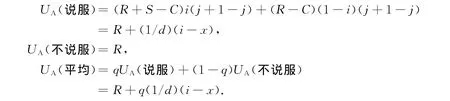
当UA（说服）不等于UA（不说服）时，得益较差的一方早晚会发现得益的差异，从而在再次面对灾害时，改变自己的策略，模仿得益较好的另一类型.因此，说服与不说服两种类型的个体的比例是随时间变化的函数，分别为q（t）和1-q（t），则说服博弈方的动态变化速度可用复制动态方程表示为［9］

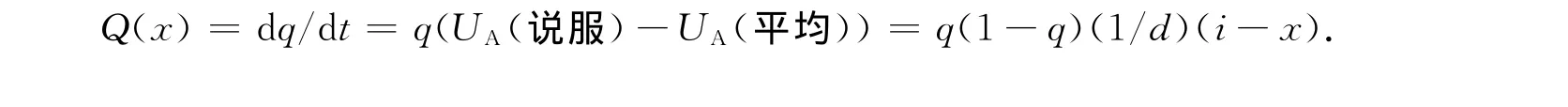
根据动态方程，如果x＝i，则dq／dt始终为0，所有q都是稳定状态，意味着只有比例为q的A类个体选择说服策略，其余个体均选择不说服策略.如果x＞i，Q（x）＜0，则q＝0，q＝1是q的两个稳定状态，其中q＝0是演化稳定状态，所有A类个体均选择不说服策略.若x＜i，Q（x）＞0，则q＝0，q＝1是q的两个稳定状态，其中q＝1是演化稳定状态，所有A类个体均选择说服策略［10］.

同理可得，B类个体的收益为

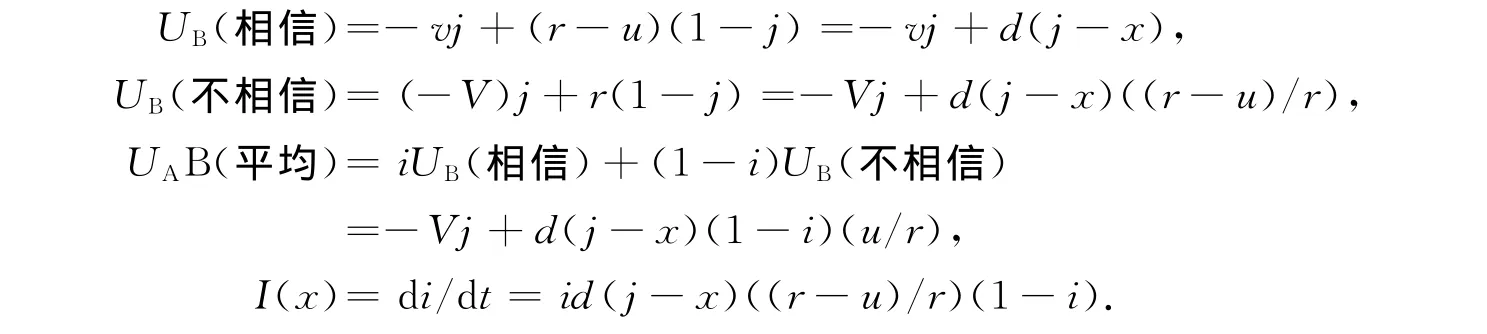
根据动态方程，如果x＝j，则dq／dt始终为0，所有i都是稳定状态，意味着只有比例为i的B类个体选择相信策略，其余个体均选择不相信策略.如果x＞j，I（x）＜0，则i＝0，i＝1是i的两个稳定状态，其中i＝0是演化稳定状态，所有B类个体均选择不相信策略.若x＜j，I（x）＞0，则i＝0，i＝1是i的两个稳定状态，其中i＝I是演化稳定状态，所有B类个体均选择相信策略.当博弈达到均衡时，也即A类和B类个体之间的观点趋向一致.

3 仿真分析

采用连续的疏散模型，利用Repast仿真工具进行仿真.A类个体的疏散观点定义在（0.5，1）区间内；B类个体的疏散观点定义在（0，1）区间内；个体个数为N.其中，A类个体占个体总数比例为y，B类个体占1-y，每个个体在初始状态随机的选择观点值，每次博弈时，在A类和B类的个体中随机选择，每个个体选择自己的观点，并进行疏散观点的交互，将相应改变自己的观点值.假设每个个体在博弈过程中所选择的观点与他们以前和其他个体交互所采取的观点所获得的收益有关.

3.1 初始情况

取N＝100，y＝0.5，R＝1，r＝0.5，V＝0.5，u＝0.21作为初始情况，疏散模型演化图如图1所示.由图1可知：随着交互次数的增加，每个个体的疏散观点会逐渐演化，收敛形成几个观点群体，经过一段时间后，最终达成观点统一，形成一个观点群体.

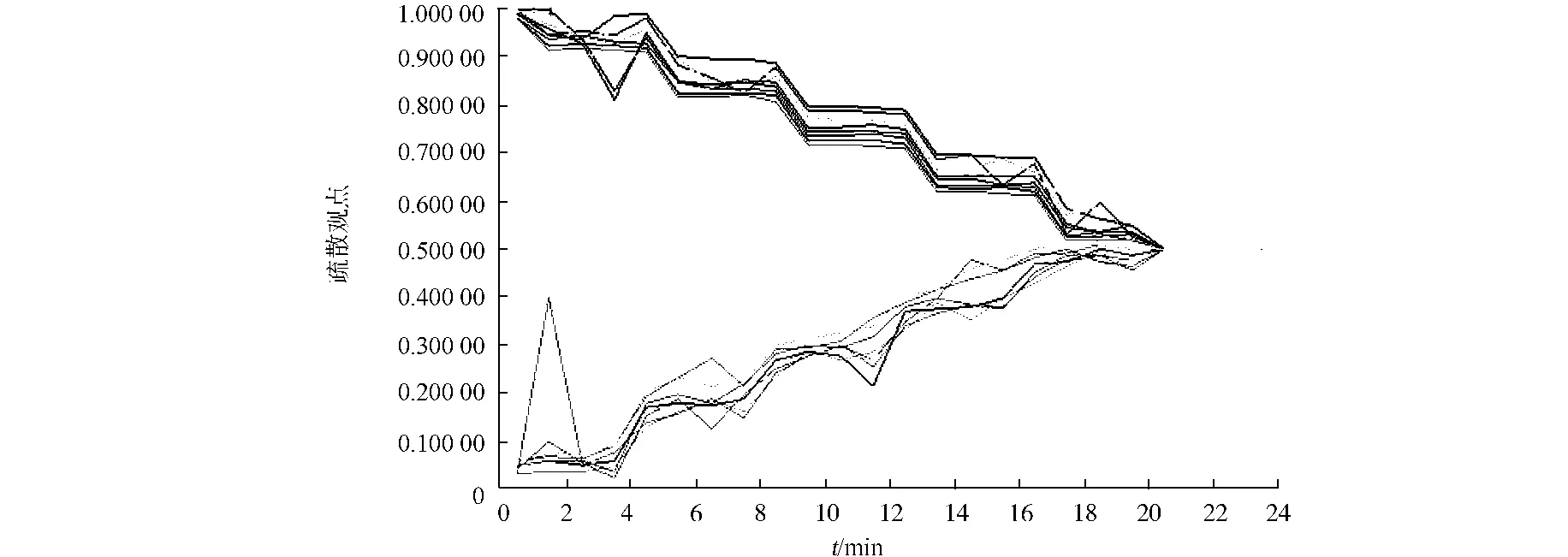
图1 初始情况疏散模型演化图Fig.1 Initial evolution chart of evacuation model

由图1中观点演化的情况表明：在刚开始的时候，由于B类个体选择相信策略的收益并不高，而A类个体为了减少不必要的损失而选择不说服策略，B类个体由于信息方面不具有优势，随机选择观点，但随着时间的推移，A类个体发现选择说服策略可以获得更大的利益，B类个体则发现选择相信策略比不相信策略的收益大，因而疏散观点逐渐演化合并，最终形成一个统一的观点.

3.2 增加B类个体选择相信策略的收益r

当增加B类个体选择相信策略的收益r，会发现收敛时间得以提前，可以更快捷有效地疏散人群.例如，取N＝100，y＝0.5，R＝1，r＝0.7，V＝0.5，u＝0.2，仿真图如图2所示.

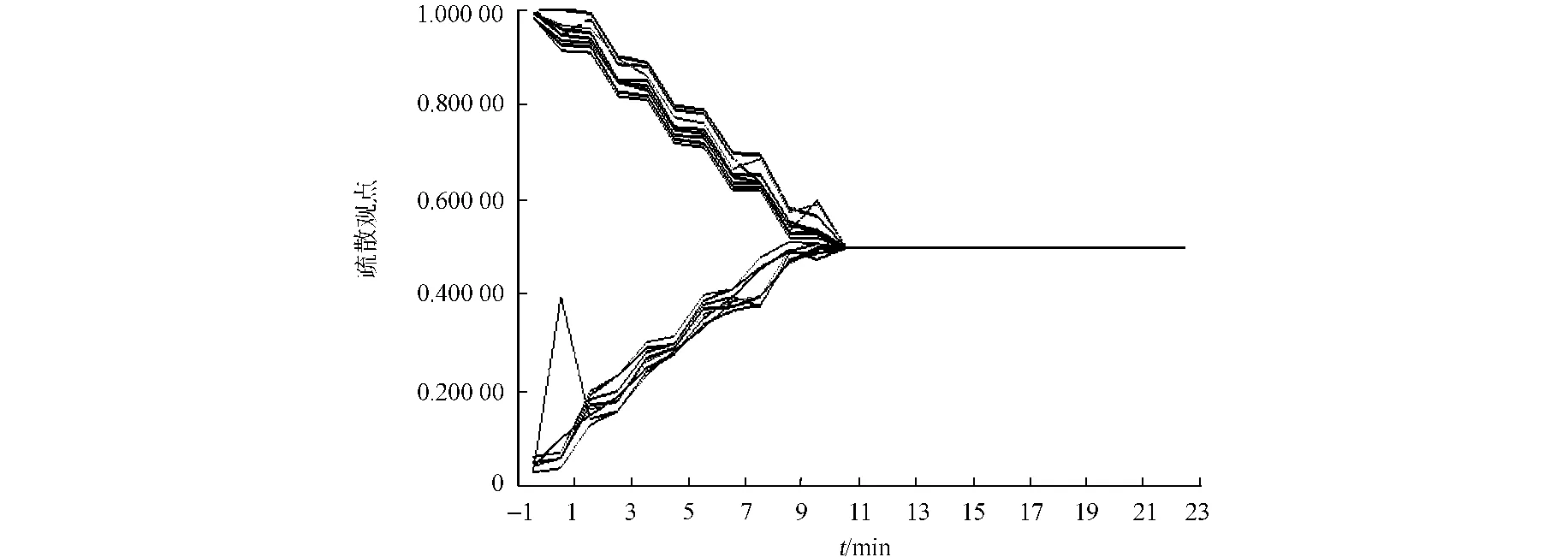
图2 增加B类个体仿真图Fig.2 Simulation of increasing agent B

由图2可知：由于B类个体选择相信策略的收益提高，所以B类个体会更多地选择相信策略，相应的，A类个体为了获得最大的收益，在一开始便大量使用说服策略，从而疏散观点的交互过程较为简单，疏散观点可以很快达到一致，交互时间得到大量减少.

3.3 减少A类个体选择说服策略的收益R

当减少A类个体选择说服策略的收益R，发现导致疏散观点一片混乱，最终没有达成一致.例如，取N＝100，y＝0.5，R＝0.5，r＝0.5，V＝0.5，u＝0.2，仿真图如图3所示.

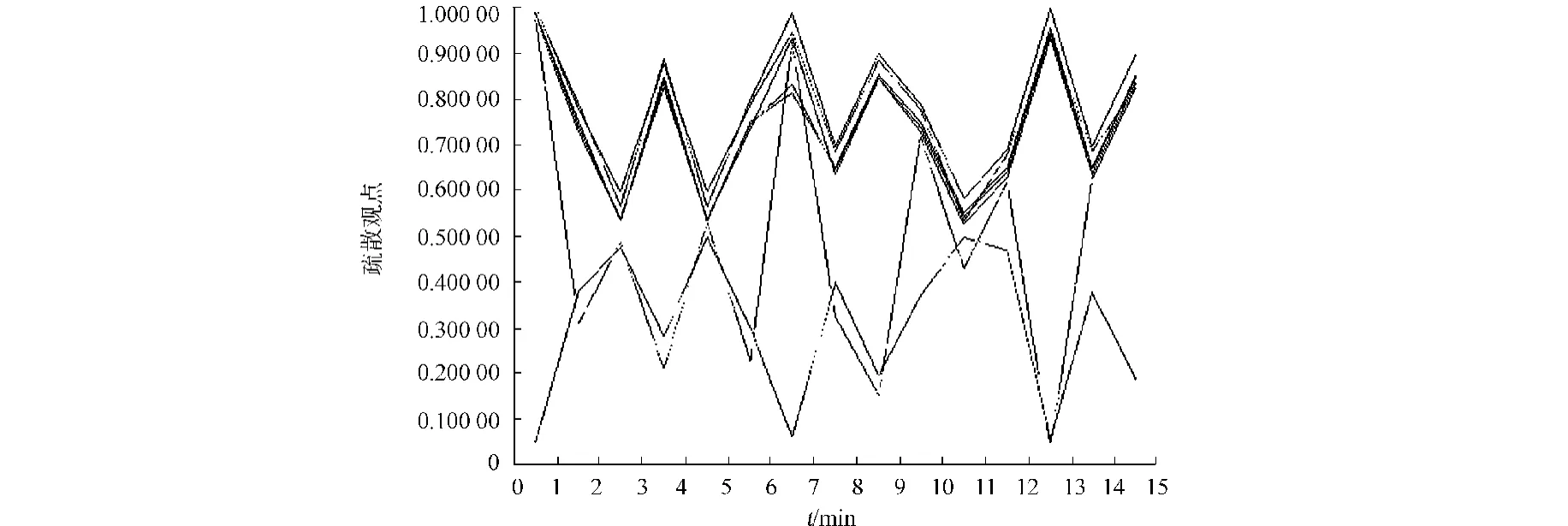
图3 减少A类个体仿真图Fig.3 Simualtion of decreasing agent A

由图3可知：由于A类个体选择说服策略的收益降低，所以A类个体出于获得最大的收益的考虑，选择说服策略的机率也大幅降低，将有大量A类个体选择不说服策略，也会有大量B类个体选择不相信策略，从而会出现多个疏散观点群体.

3.4 疏散观点收敛时间与A，B两类个体比例的关系

疏散策略收敛的时间与A，B两类个体的比例有直接的关系，例如，当分别取y＝0.3，y＝0.5，y＝0.7，而其他参数不变，即N＝100，R＝1，r＝0.5，V＝0.5，u＝0.2，仿真图如图4所示.图4中：n为仿真次数；t为收敛时间.

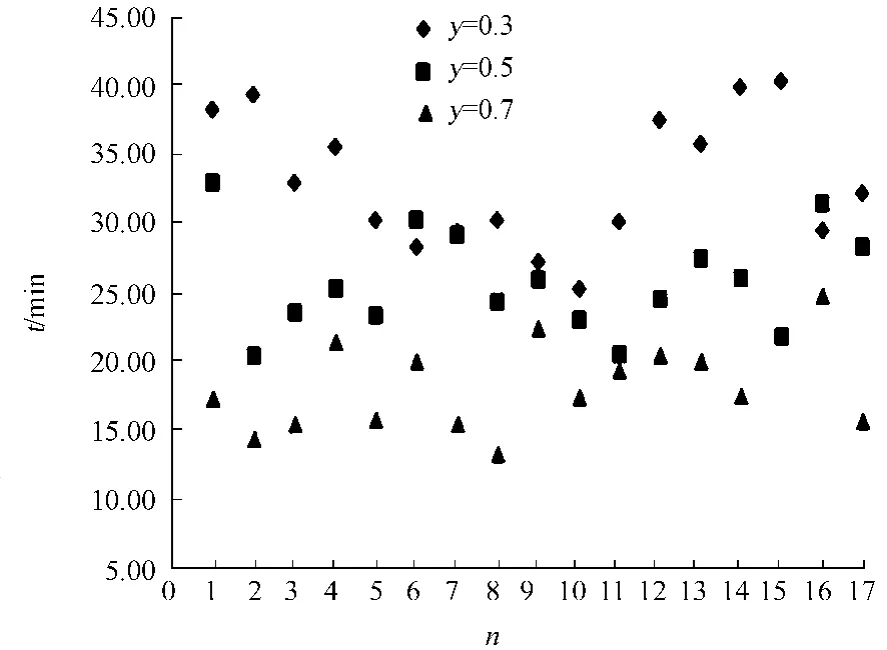
图4 y对收敛时间的影响Fig.4 Influence of yon convergence time

由图4可知：随着A类个体占总体比例的减少，即对信息拥有优势的个体在人群中的比例的减少，遇到的选择相信策略的B类个体的概率也降低，从而造成疏散观点收敛时间变长，疏散时间也相应变长，反之则变短.

4 结论

将个体异质性引入个体的行为中，提出演化博弈收益函数，模拟仿真博弈模型，得到以下4点结论.

1）由于受教育程度和社会关系等因素的不同，受灾人员中必然会有一些人具有信息优势，当其中一部分人发现适当透露自己已知的信息去说服别人可能获得超额利益，他们可能会继续采取说服策略.

2）信息劣势者发现选择相信后能够提高收益，减少损失，会继续相信并吸引更多人追随前者，反过来也激励更多信息优势者选择说服策略，从而实现博弈均衡.

3）提出一个基于演化博弈论的灾害人员疏散仿真模型，与其他的人员疏散仿真模型不同的是，考虑了个体的消息不对称问题，通过个体的不同选择，使得模型可以更好地研究个体行为对逃生结果的影响，从而制定出更加有效的疏散方案.

4）不同策略的收益、具有信息优势者的比例等因素均对灾害人员的疏散过程有着显著的影响.

［1］ 彭华，许斌，罗灿华，等.一种基于几何方法的人员疏散多威胁规划算法［J］.建筑科学，2010（3）：84-86.

［2］ 李俊.体育场馆人员疏散时间数学模型研究［J］.哈尔滨商业大学学报：自然科学版，2011，27（2）：13-20.

［3］ 周金旺，陈秀丽，孔令江，等.基于元胞自动机的行人流疏散模拟研究［J］.广西师范大学学报：自然科学版，2008，26（4）：14-17.

［4］ 宋伟，李美彦，胡晓琴.基于元胞自动机的人员疏散微观仿真［J］.交通科技与经济，2011，65（3）：85-88.

［5］ 任书君，汪波，欧阳朝辉，等.基于Agent和元胞自动机的人员疏散过程建模与仿真［J］.福建电脑，2011，27（3）：99-101.

［6］ 何大治，谢步瀛.基于子空间网络的人员疏散模型［J］.工程图学学报，2009，12（2）：24-26.

［7］ 韩少春，刘云，张彦超，等.基于动态演化博弈论的舆论传播羊群效应［J］.系统工程学报，2011，26（2）：275-281.

［8］ 夏茂森，朱宪辰，江波，等.农产品交易行为的动态演化博弈分析［J］.技术经济，2009，28（8）：123-127.

［9］ BRAUER F，DRIESSCHE P.Models for transmission of disease with immigration of infectives［J］.Mathematical Biosciences，2001，171（2）：143-154.

［10］ 朱孔金，杨立中.房间出口位置及内部布局对疏散效率的影响研究［J］.物理学报，2010，59（11）：7701-7707.