涉及微分多项式的亚纯函数族正规定则
孟耀霞, 刘晓俊
(上海理工大学 理学院,上海 200093)
1 问题的提出
1986年,杨乐[1]和朱经浩[2]证明了定理1.
定理1 设F为区域D内的亚纯函数族,ψ≠0为D内的全纯函数,k∈Z+.如果每个f∈F,在D内都满足f≠0与L(f)≠ψ(z),则F在D内正规.
2010年,徐焱[3]进一步得到了定理2和定理3.
定理2 设k∈Z+,F为区域D内的亚纯函数族且对每个f∈F满足f≠0,ψ≠0为D内的全纯函数.如果对F内任一组函数f与g,f(k)与g(k)在D内分担ψ(z),则F在D内正规.
定理3 设ψ≢0为区域D内的只有单零点的全纯函数,k∈Z+,F为区域D内的亚纯函数族.如果每个f∈F满足f≠0且只有重极点;对F内任一组函数f与g,f(k)与g(k)在D内分担ψ(z),则F在D内正规.
本文将定理2和定理3推广到微分多项式[4]的情形,得到了定理4和定理5.
定理4 设k∈Z+,F为区域D内的亚纯函数族且对每个f∈F满足f≠0,ψ≠0为D内的全纯函数.如果对F内任一组函数f与g,L(f)与L(g)在D内分担ψ(z),则F在D内正规.
定理5 设ψ≢0为复平面区域D内的只有单零点的全纯函数,k∈Z+,F为区域D内的亚纯函数族.如果每个f∈F满足f≠0且只有重极点;对F内任一组函数f与g,L(f)与L(g)在D内分担ψ(z),则F在D内正规.
Pf表示f的极点,C\Pf表示复平面C除掉f的极点.
2 引 理
引理1[5]设F为区域D内的一个亚纯函数族,每一个f满足f≠0.如果F在D内的一点z0不正规,则对任何的α≥0,存在
a.点列zn→z0(n→∞);
b.正数列ρn→0+(n→∞);
c.函数列fn∈F,使得这里g(ζ)为非常值有穷级亚纯函数.
引理2[6]设f为复平面C上一个非常值亚纯函数,a≠0∈C,k∈Z+,则f或f(k)-a有零点.更进一步,若f是超越亚纯函数,则f或f(k)-a有无穷多个零点.
引理3[3]设k∈Z+,f为非常值有理函数且f≠0,则
a.f(k)(z)-1至少有2个不同的零点;
b.若f的极点均为重级(至多可能有1个例外),则f(k)(z)-z至少有2个不同的零点.
引理4[7]设f为复平面C上的一个超越亚纯函数,R(z)≢0为一有理函数,k∈Z+.如果f的零点与极点(除有限个外)重级都至少为2,则f(k)-R有无穷多个零点.
由定理4和文献[3]中引理7~9的证明过程得到引理5~7.
引理5 设k∈Z+,F为区域D内的全纯函数族且任意的f∈F,ψ≢0为D内的全纯函数.如果对F内任一组函数f与g,L(f)与L(g)在D内分担ψ(z),则F在D内正规.
引理6 设k∈Z+,F为区域D内的亚纯函数族,{ψn(z)}为D内全纯函数列且在D上内闭一致收敛到全纯函数ψ,满足ψ(z)≠0(z∈D).如果对每个n,fn(z)≠0且L(fn)(z)-ψn(z)在D内至多只有1个零点z=0,则F在D内正规.
引理7 设k,l∈Z+,Δ=f{}n为Δ内的全纯函数族,为Δ内纯函数列且在Δ上内闭一致收敛到zl,如果对每个n,有fn(z)≠0与L(fn)(z)-ψn(z)在Δ内至多只有1个零点z=0,则F在Δ内正规.
3 定理的证明
3.1 定理4的证明
假设 F在点z0∈D不正规,由引理1可知,存在点列zn→z0,ρn→0+及fn∈F,使得gn(ζ)=在C上,这里g(ζ)为非常值有穷级亚纯函数.因为,fn≠0,所以,由Hurwitz引理得g(ζ)≠0,易得,在C\Pg上

由式(1)可知,在C\Pg上
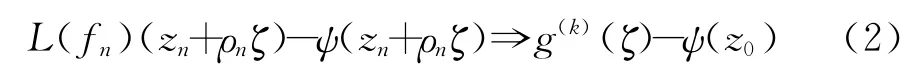
g(k)(ζ)-ψ(z0)≢0;否则,G为一个k次多项式,但这与G(ζ)≠0矛盾.
若∃ζ0,使得g(k)(ζ0)=ψ(z0),由引理2和引理3可知,g(k)(ζ)-ψ(z0)至少有2个不同的零点,现证明这是不可能的.
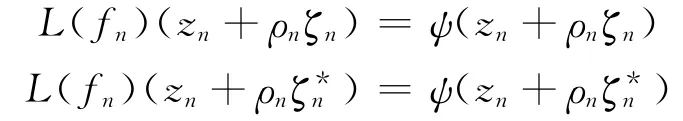
由定理4中的条件可知,对任何fm∈F也有

固定m,令n→∞,有及L(fm)(z0)-ψ(z0)=0.可设在z0的某领域内L(fm)(z)-ψ(z)≢0.否则,存在z0的某领域,使得在这个领域内L(fm)(z)≠ψ(z)+1,于是,由定理1可知,F在点z0∈D正规,与假设矛盾.这样由上可推得zn+ρnζn=z0与,但这与矛盾.
若g(k)(ζ)≠ψ(z0),由引理2可知,g(ζ)为常值函数,矛盾.
3.2 定理5的证明
由定理4的结论可知,只需证明F在ψ(z)的每个零点处正规即可.
不失一般性,可设D=Δ,ψ(z)=zφ(z)(z∈Δ),这里φ(z)为Δ内的全纯函数,且在Δ上φ(z)≠0,φ(0)=1.只要证明F在点z=0正规.
若∃g∈F,使得L(g)(0)≠ψ(0),则存在δ>0使得在Δδ上L(g)(z)≠ψ(z).由定理5中的条件可知,对任意f∈F,在Δδ上有L(f)(z)≠ψ(z).根据定理1可知,F在点z=0正规.
若对∀g∈F,L(g)(0)=ψ(0),取定1个g∈F,L(g)(0)=ψ(0),∃δ>0使得L(g)(z)≠ψ(z),z∈Δ′δ;否则,在该领域内有L(g)(z)≡ψ(z),由定理5中的条件可知,对任意f∈F,同样有L(f)(z)≡ψ(z).这样,在z=0的该领域内有L(f)(z)≠ψ(z)+1,应用定理1,F在点z=0正规,定理5得证.从而对∀f∈F,有
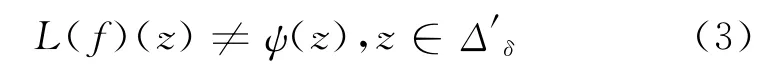
由定理1可知,F在Δ′δ正规.
假设F在点z=0不正规.考虑

因为,f≠0,所以,g(0)=∞.此时G在z=0也不正规.
由引理1可知,存在zn→0,ρn→0+及gn∈G,使得在C上,这里G(ζ)是C上一个非常值有穷级亚纯函数.因为,gn=fn/ψ≠0,所以,由 Hurwitz定理可知,G(ζ)≠0.
情形1zn/ρn→∞.
通过简单计算可得

设
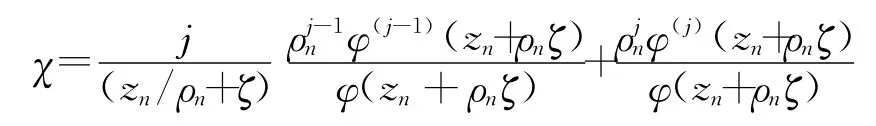
于是


则


所以

由G(ζ)≠0,易知G(k)(ζ)≢1.进一步可断言,G(k)(ζ)≠1.事实上,若G(k)(ζ0)=1,则由 Hurwitz定理可知,存在ζn→ζ0,使得对充分大的n,L(fn)(zn+ρnζn)=ψ(zn+ρnζn),从而由定理5中的条件可知,对每个正整数m都有L(fm)(zn+ρnζn)=ψ(zn+ρnζn).另外,zn+ρnζn→z0∈Δδ,则对充分大的n,zn+ρnζn≠0;否则zn+ρnζn=0,从而ζn=-zn/ρn→∞,矛盾.这样对充分大的n,zn+ρnζn∈Δ′δ.这与式(3)矛盾.
于是,有G(ζ)≠0与G(k)(ζ)≠1.由引理2得G是常数,矛盾.
情形2zn/ρn→α≠∞.
令

显然H(0)≠0,并且由fn≠0及Hurwitz定理可推得H(ζ)≠0.因为,fn只有重极点,同样由 Hurwitz定理可得,H也只有重极点.而

由式(4)得,在C\PH上,

故

断言:当ζ∈C\{0}时,H(k)(ζ)≠ζ.
首先,H(k)(ζ)≢ζ.否则,H(k)(ζ)≡ζ,则H是次数为k+1的多项式,从而与H≠0矛盾.如果存在ζ0≠0使得H(k)(ζ0)=ζ0,由 Hurwitz定理与式(5)可知,存在ζn→ζ0使得即L(fn)(ρnζn)=ψ(ρnζn).
由定理5中的条件,对每个正整数m都有L(fm)(ρnζn)=ψ(ρnζn),ρnζn∈Δ′δ,这与式(3)矛盾,断言得证.
注意到H(ζ)≠0,由引理4可得,H必为有理函数.如果H不是常数,应用引理3可得,H(k)(ζ)-ζ至少有2个不同零点,矛盾.因此,H为一非零常数.现证明这是不可能的.
若设H≡C≠0,则有
若存在δ1>0,使得fn≠∞,z∈Δδ1,则由引理5可知,{fn}在Δδ1上正规,矛盾.
故

若存在ζ0(≠0)使得H*(k)(ζ0)=ζ0,则由Hurwitz定理可知,存在ζn→ζ0使得ζn=ζnφ(z*nζn),即
由定理5中的条件可知,对每个正整数m都有但这与式(3)矛盾.故对每个至多在C上有一个零点ζ=0,设则在Δ上内闭一致收敛,有ψn(ζ)→ζ.应用引理 6 得在C\{}0上正规.注意到z*n为fn具有最小模的极点,则在Δ上全纯,可应用引理7得在Δ上正规.因此,在整个C上正规.
[1]Yang L.The normality of meromorphic fuctions[J].Science in China(Seris A),1986,29(9):897-908.
[2]Zhu J H.A general normal criterion of meromorphic functions[J].Bullen of Science(Chinese),1986(3):174-177.
[3]Xu Y.On a result due to Yang and Schwick[J].Sci Sin Math,2010,40(5):421-428.
[4]翟文娟,叶亚盛,宋红伟.涉及微分多项式的亚纯函数正规性[J].上海理工大学学报,2009,31(2):122-124.
[5]Zalcman L.Normal families:new perspectives[J].Bull Amer Math Soc,1998,35(3):215-230.
[6]Hayman W K.Meromorphic Functions[M].Oxford:Clarendon Press,1964.
[7]Pang X C,Zalcman L.Normal families and shared values[J].Bull London Math Soc,2000,32(3):325-331.

