全焊接板壳式换热器入口处温度的数值模拟

施卿海， 苏文献， 许 斌， 范 斌

（上海理工大学 能源与动力工程学院，上海 200093）

全焊接板壳式换热器是芬兰伐德鲁斯公司最早发明的新一代换热器，其核心是由波纹换热板片经本体焊接而成的换热板束，外壳是压力容器.由于其具有紧凑、高效、无密封垫片、耐高温、耐高压等优点［1］，近年来被国内外广泛使用.在国内由于生产环境以及制造工艺的不同，使得这种换热器的寿命相比国外大大减小，究其原因是由于在过热蒸气进口处的板束温差应力过大而加剧板束的损耗造成的.因此，对此处的温度分布进行分析研究是改善这种情况的重要方法之一.近年来，随着数值计算技术和湍流模拟理论的迅速发展，利用数值方法对换热器的研究越来越多，在国内如刘利平等［2］采用FLUENT软件对管壳式换热器壳程三维流场进行了模拟研究，但对于全焊接板壳式换热器方面的研究至今未见报导.为此，采用FLUENT软件对HYBIRD全焊接板壳式换热器过热蒸汽进口处的温度进行模拟分析，通过改变进口的流量、直径进行对比分析，从而进一步揭示过热蒸汽入口处板束温度的分布状况，为其优化设计提供直观信息.

1 数值计算模型

1.1 换热器整体模型

HYBIRD全焊接板壳式换热器近几年来在工业中特别是电力企业得到广泛应用，其内部流体示意图见图1.两块波纹板之间的通道形成板程，板束与板束之间焊接而形成的一个个小孔为壳程，两者形成十字错流.从图1中可以看出，几乎整个金属板表面都用于热交换，使得板壳式换热器内部的死点数量大大减少，提高了换热器的换热效率.图2为换热器整体结构图.

图1 内部流体示意图Fig.1 Schematic diagram of internal fluid

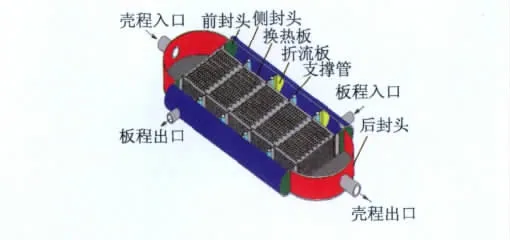
图2 换热器结构图Fig.2 Structure chart of heat exchanger

由于受计算机硬件等因素的制约，很难对一台完整的换热器模型进行计算，需对几何模型进行简化，模型的简化主要是利用相似原理和主要矛盾分析方法，选取最能代表换热器特征参数变化规律的区域进行分析求解，因而作者对换热器的板束、折流板数目以及结构尺寸都进行了一定的简化.图3为在Gambit中建立换热器模型的整体结构图，表1为换热器的结构尺寸.

图3 换热器模型图Fig.3 Model of heat exchanger

表1 换热器的结构尺寸Tab.1 Structural dimensions of the heat exchanger

1.2 模型选择及控制方程组

全焊接板壳式换热器的数值计算，由于换热器壳程结构复杂以及流动形态多样化，使得影响流体流动和传热的因素增多.考虑到湍流效应对流动与传热的影响，故采用κ－ε湍流模型进行模拟，而其中的RNG（renormalization－group）模型可以更好地预测靠近壁面处和高流线曲率流体的流动状态，所以选择κ－ε（RNG）模型.为了便于分析设定：流体为牛顿流体、流体物性为常数及流体横向导热忽略不计［3］.换热器流体的流动和热量传递必须满足方程：

式中，xi为x方向的位移分量；ρ为流体密度；ui为x方向的速度分量.

式中，uk为y方向的速度分量；μ为流体黏度；p为流体微元体上的压力；xk为y方向的位移分量.

式中，t为时间；k为传热系数；Cp为比定压热容.

湍流动量方程

式中，μeff为有效动力黏度；Gk为平均速度梯度引起的湍动能k产生项；ε为湍动耗散率.

能量耗散方程

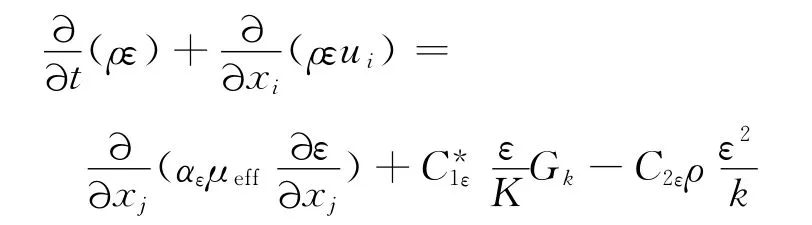
其中

以上式中，αε＝1.39；C1ε＝1.42；C2ε＝1.68；η为卡诺循环效率.

1.3 计算方法和边界条件

采用Gambit软件建立模型和划分网格，由于全焊接板壳式换热器壳程结构复杂，所以采用四面体和金字塔网格来划分.在FLUENT中采用分离变量法隐式求解，保证收敛的稳定性.压力和速度耦合 采 用 SIMPLE （semi－implicit method for pressure－linked equation）算法，动量、能量以及湍流参量的求解采用二阶迎风格式，质量及能量计算残差控制在10－4数量级之内.

计算流体进口壳程采用质量流速进口，板程采用速度进口，按流体质量流速、速度、温度、湍流强度等分别给定壳程和板程入口条件；出口为压力出口边界条件；板壁、折流板采用热耦合边界条件；壳体壁面采用绝热边界条件.壁面边界采用无滑移固壁条件，并使用标准壁面函数法确定固壁附近流动.

壳程过热蒸气进口质量流速Ms为0.01kg／s，温度为500K；板程水进口流速为2m／s，温度为330K.

2 计算结果及数据处理

2.1 壳程温度

图4为换热器壳程的温度云图.图中可以看出温度沿壳程流向逐渐减小，且随折流板个数的增加，温度的下降幅度逐渐变小.特别在入口处的红圈里温度分布很不规则，这是由于流体刚进入时的不确定性，使得在进入板束中间通道的时候造成流量分布不均，久而久之这种分布导致了温差应力慢慢增大，从而减少了换热器的使用寿命，这也是现在国内对于HYBIRD全焊接板壳式换热器方面一个没有解决的难点.为此将改变过热蒸气流量以及直径进行进一步研究分析.

图4 壳程温度分布云图Fig.4 Temperature contours of the shell

2.2 板束在不同进口质量流速情况下的温度

图5（见下页）为进口处板束在质量流速Ms分别为0.002，0.005，0.008和0.01kg／s情况下的温度分布云图.图中可以看出随着质量流速的增大，板束间的温差也越来越大.图5（a），5（b）可以看出当质量流速较小时，各个板束间的温度分布比较均匀，温差也比较小；图5（c），5（d）可以看出中间两块板束的温度较高，而上下两块板束的温度则相对比较低，过大的温度差将导致温差应力增大，加剧板束的破坏.

2.3 板束在不同进口直径情况下的温度

图6（见下页）为进口直径分别为20，40，60和80mm情况下的温度分布云图.图中可以看出随着过热蒸气入口直径的增大，板束间的温差逐渐减小.当直径为20mm时，造成入口处板束中心温度过高，换热面积过小，使得板束都没有充分地参与到换热中去，大大增加了能耗，因此是非常不合理的；当直径为40mm时，同一板束间的两边温差也越来越大；当直径为60mm时，中间板束与两边板束的温差加大；当直径为80mm时，各板束间的温度基本相同，这样使得温差应力大大减小.

图5 不同质量流速下入口处板束的温度分布图Fig.5 Temperature contours at the entrance of plates with different mass flow rates

图6 不同进口直径入口处板束的温度分布图Fig.6 Temperature contours at the entrance of plates with different diameters

2.4 结果对比分析

图7为同一板束以及不同板束的最大温差随着过热蒸汽质量流速和入口处开孔率变化情况.图中可以看出随着质量流速的减小以及入口处开孔率的增大，同一板束以及不同板束间的温差逐渐减小.

图7 不同质量流速和不同开孔率变化时的温差Fig.7 Curve of differential temperature with different mass flow rates and percentage of open area

这里，过热蒸汽入口直径与换热器壳体截面长度之比可以作为此换热器的开孔率φ＝Di／a，Di为过热蒸汽进口直径，mm；a为换热器长方体外壳的宽度，mm；可以看出随着开孔率的逐渐增大，入口处板束温度分布越来越均匀.

另外，忽略板束内流体受内压后的轴向应力，只考虑板束间温差引起的温差应力.板束不受约束时，因温差而引起的自由伸长量为δ＝α（tmax－tmin）L，由于板束间刚性连接，根据胡克定律，可得出温差应力与伸长量间的关系为δ＝FL／EA，故温差应力F＝αEA（tmax－tmin）.而tmax－tmin与过热蒸汽质量流速和换热器的开孔率有关，假定温差与质量流量成正比，与开孔率成反比，则F＝αEAβMS／φ＝γEAMS／φ.其中α为管和壳在平均壁温下的线膨胀系数，1／℃；L为板束长度，mm；E为板束弹性模量，MPa；A为板束横截面积，mm2；β为温差应力系数；γ为总温差应力系数.

根据前面的分析，全焊接板壳式换热器的开孔率应在70%左右合适；而且入口的质量流速也应该适中，过大会导致温差应力增大，过小会使换热速度减慢，从而影响工艺流程.所以在确定开孔率的情况下设计出合理的质量流速是保证换热器正常工作的最主要因素.

3 结 论

a.全焊接板壳式换热器温度沿壳程流向逐渐减小，且随折流板个数的增加，温度的下降幅度逐渐变小，而且在入口处的温度分布很不规则.

b.随着过热蒸汽入口质量流速的增大，同一板束以及各个板束间的温差也越来越大.

c.随着过热蒸汽入口直径的增大，同一板束以及各个板束间的温差越来越小.

d.温差应力与壳程入口的质量流速成正比，与开孔率成反比，在设计时，开孔率在70%左右较为合适，质量流速应在保证工艺要求的情况下尽可能的减少.

［1］李含苹.全焊接板壳式换热器在传热中的应用［J］.船舶，2004（4）：35－38.

［2］刘利平，黄万年.FLUENT软件模拟管壳式换热器壳程三维流场［J］.化工装备技术，2006（3）：54－57.

［3］王艳云，李志安.FLUENT软件对管壳式换热器壳程流体数值模拟方法可行性的验证［J］.管道技术与设备，2007（6）：46－48.

［4］Ozden E，Tari L.Shell side CFD analysis of a small shell－and－tube heat exchanger［J］.Energy Conversion and Managemant，2010，51（5）：1004－1014.