氨水溶液密度计算与实验分析
陈小砖, 柳建华, 张 良, 刘 旗, 张美鑫
(1.上海理工大学 能源与动力工程学院,上海 200093;2.河南理工大学 机械与动力工程学院,焦作 454003)
1 问题的提出
随着人们对环境和能源问题的日益重视,面对日益严峻的全球变暖和极端天气的频频出现,加上对臭氧层破坏的关注,天然制冷剂受到了前所未有的重视.其中氨制冷剂由于自身的特性,在很多领域重新受到青睐.氨来源于自然界,其臭氧层损耗潜能值和全球变暖潜能值均为零,符合当今节能减排和可持续发展的要求.氨水吸收式制冷可以利用余热制取0℃以下的低温冷量,可以应用在制冰或其它特殊的低温工艺中.在氨水吸收式制冷计算中,经常需要求出氨水溶液某一状态点的相关参数,如密度、焓及熵等,目前很多设计计算是查氨水的焓浓度图求取氨水的物性参数.由于图上的压力线和温度线都不是连续的,加上看图需要人为观察估计,获取的参数和真值有一定误差,因此,缺乏精度高的氨水状态方程制约着对氨水吸收系统精确的计算与优化.虽然目前有学者推荐几个精度高的方程,使用其可以计算饱和液体的密度,但没有具体的计算方法,尤其缺乏详细的适应条件说明和误差分布研究[1-2].如果有一些对氨水工质计算的高精度状态方程存在,就可以利用现代高速计算机对氨水吸收式制冷系统进行计算与模拟,提高氨水吸收式制冷系统的制冷效率[3].
氨和水的物理化学性质同它们的分子结构有特定的联系,在计算其物性参数之前有必要了解分子内与分子间的作用力关系.水分子中氧原子与氢原子之间形成极性共价键,而氨分子中氮原子和氢原子也形成极性共价键[4].由于氨与水分子内部这种特殊的极性共价键的存在,它们分子之间形成氢键.图1显示氨与水分子的路易斯结构及结构式.氢键是一种存在于相邻分子间、带异性部分电荷原子间的静电吸引力.典型的氢键强度大约是分子内连接原子的共价键强度的1/10,键长也相对较长.虽然氢键强度不如共价键那样强,但与其它类型的分子间作用力相比,其强度依然很大.理解氢键的形成对认识、分析氨和水的物理化学性质具有至关重要的意义[5].综上所述,氨和水都是极性物质,并且分子之间有氢键形成,所以,适合描述氨和水物性的状态方程比较少.先后经过Yamada,Gunn和Campbell改进的Rackett方程[6],计算精度有了进一步的提高.P-R方程有很高的计算精度,特别是对饱和蒸汽压、气液相密度等的计算.1973年,Schulz发表了氨及氨水溶液的吉布斯自由能表达式[7],在此基础上,利用热力学基本关系式可以获得氨水体系的相平衡状态方程和焓浓度关系式.但该方程参数太多,相当繁琐,非专业人士难以使用.马丁-侯方程是美国学者马丁和我国学者侯虞钧于1955年提出的,简称M-H方程,1981年侯虞钧等又将方程的适用范围扩展到液相区,很多文献已经证明了M-H(81)型方程能够较好地适合极性物质的计算[8-10].但该方程参数过多,而且每一种物质的参数要单独确定,所以,仅适用于一些特定场合,如合成氨的工艺计算等.虽然在文献找到了几个可以计算极性物质的方程,但没有看到对这些方程的适用条件、计算精度等方面的定量描述,所以,非常有必要去研究适合氨和水的高精度的方程,并对其应用范围和使用方法进行系统研究.

图1 氨分子和水分子的路易斯结构图Fig.1 Lewis structures of ammonia molecule and water molecule
2 氨和水纯组分液体密度方程
通过查找相关文献,最终选择P-R方程、Rackett方程[11]、Campbell改进的 Rackett方程和Yen-Woods关系式[12]来计算氨和水的饱和液体密度.计算液体氨的密度,选择温度变化区间为-30~55℃,而对于水选择温度区间为6~100℃.氨和水的基本物性参数和临界参数如表1所示.现分别介绍这些公式的具体形式、求解需要输入的参数和求解方法.

表1 氨和水的物性参数Tab.1 Physical property parameters of water and ammonia
2.1 Yen-Woods关系式

式中,Kj为临界压缩因子Zc的函数.
该方程计算时只需要输入温度、临界密度和临界压缩因子Zc,即可求出饱和液体的密度.
2.2 Rackett方程

只需要给出临界压缩因子,即可利用该公式求出任意温度下的饱和液体摩尔体积.求出摩尔体积后,再给出分子量,即可求出密度.
2.3 Campbell改进的Rackett方程
Campbell等对Rackett方程作了一系列改进,计算精度有了很大的提高,方程形式为

式中,α,β为常数,对于氨分别为 0.246 3 和0.002 7,对于水分别为0.225 1和0.032 1[6].
该方程的形式比较简单,求解也很方便.只需输入温度和临界状态的参数,即可求出饱和液体的,摩尔体积.再给出分子量,就可求出密度.
2.4 P-R方程
P-R方程由Peng和Robinson于1976年提出,也是一个两常数方程,简称P-R方程[12],是对范德瓦尔斯方程和R-K方程的进一步修正,其表达式为
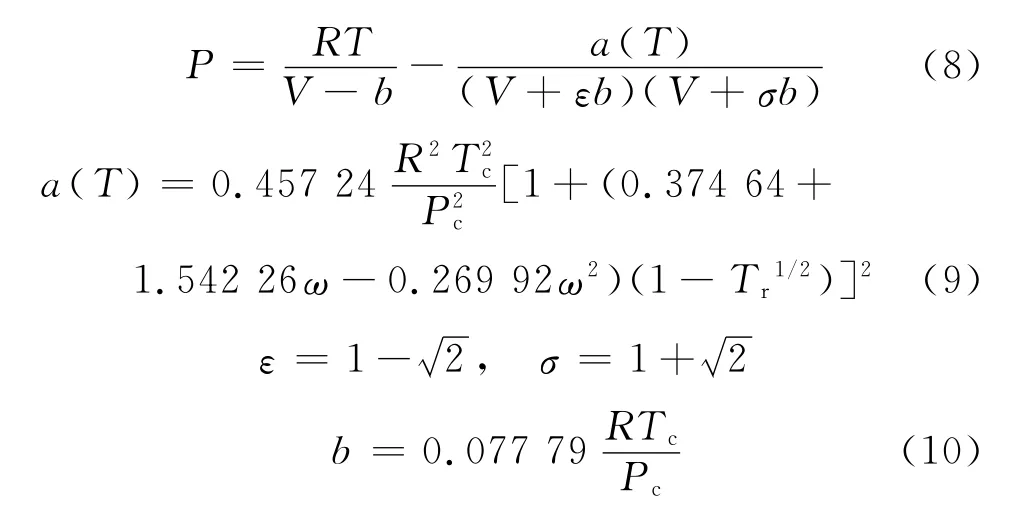
利用P-R方程求解饱和液体的密度可以采用迭代法.
分别应用上述不同的方程形式,利用Matlab 7.0软件对氨和水纯工质计算不同温度下的饱和液体密度[13].Yen-Woods关系式直接按照其方程形式代入相关数据计算,P-R方程运用前面介绍的迭代形式,编制一个函数循环迭代,收敛后求出密度.Rackett方程及其改进方程形式简单,所需要的参数较少,只要给出所求工质的临界温度和临界摩尔体积,还有临界压缩因子,即可求出不同温度下的液体密度.
3 纯组分密度计算结果
利用 Matlab7.0软件作为计算工具[13],编制程序然后求出不同方程下氨或水的饱和液体密度.最后将不同方程的计算结果与不同温度密度的标准值对比,求出不同温度点的相对误差,计算所有温度点的平均相对误差.相对误差等于密度的标准值与计算值之差的绝对值再除以标准值得到的百分率.密度的标准值可以查阅文献[14]附表1和附表2中氨和水饱和液体热力性质.将不同温度点的密度值导入到Excel中,绘成折线图,可以在图上非常清楚地看到不同方程形式计算结果的精度和误差大小.
对于氨选择的温度区间为-30~55℃.从图2可以看出,P-R方程的密度计算结果平均误差为11.24%,误差最大.Rackett方程平均误差为3%.Yen-Woods关系式计算的密度值平均误差为0.73%,最大误差出现在温度55℃点,为1.32%;不同温度点上的密度误差随温度增加递增,-30℃的误差为0.16%.Campbell改进的Rackett方程平均误差为0.38%,最大误差出现在-30℃温度点,为0.41%.不同温度点上的密度误差随温度增加递减.可以看出,Campbell改进的Rackett方程在强极性液体密度计算方面是一个高精度的方程.
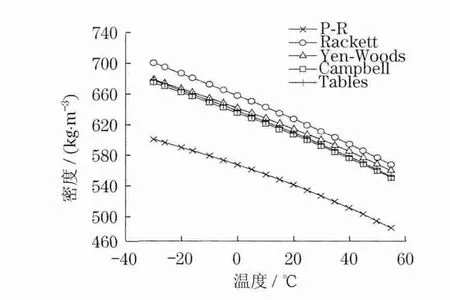
图2 氨饱和液体密度随温度变化Fig.2 Density of saturated liquid ammonia versus temperature
对于水选择的温度区间为6~100℃.从图3可以看出,误差最大的还是P-R方程,密度平均误差为15.12%.Rackett方程平均误差为9.45%.Yen-Woods关系式计算的其密度值平均误差为1.38%,在6℃的误差最大,为3.59%;最小误差出现在76℃点,为0.056%.计算精度最高的是Campbell改进后的Rackett方程,在整个温度区间,其平均误差为0.58%,最大误差出现在100℃点,为1.01%;最小误差出现在30℃点,为0.01%.
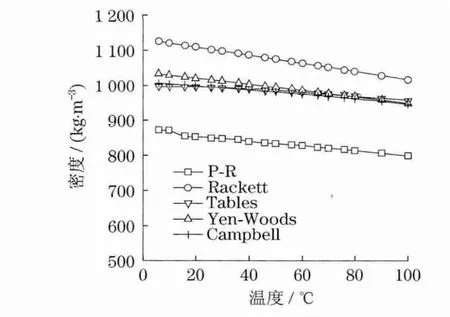
图3 饱和水密度随温度变化Fig.3 Density of saturated liquid water versus temperature
4 氨水溶液密度计算
4.1 理论计算方法
利用前面介绍的方程可以分别求出某一温度下氨和水纯组分的密度,如果给出它们在溶液中的摩尔分数,就可以根据流体的混合性质计算出混合后氨水溶液的摩尔体积[15].密度是摩尔体积和相对分子质量的函数,求出摩尔体积后,密度随之求出[12].

摩尔体积的超额函数的性质和相应的混合性质类似.
式中,活度系数GE/RT是T,P及组分的函数,但是,对于低压至中压下的液体,它只是微弱的压力函数,因此,活度系数随压力的变化常可被忽略,即VE/RT为0.于是,代入到式(11)求得混合后的摩尔体积为

4.2 实验方法
4.2.1 采用氨水溶液密度计测量
目前市场上有针对腐蚀性液体研发的高精度密度计,可以用于氨水溶液的测量.北京仪特诺电子科技有限公司生产的氨水密度计非常适合测量氨水这类碱性溶液的密度,如图4所示.该产品的密度量程为200~1 800kg/m3,精度为1kg/m3.测量范围正好适合氨水溶液的密度测量,而且精度还是较高的.测量氨水溶液密度时有两个要点需要特别注意:一个是要精确测量待测溶液的温度,取样后尽可能地快速测量密度,防止溶液受外界环境温度的干扰;另一个是采取措施减少或避免氨水溶液的挥发,如降低测量点的局部风速等[16].
4.2.2 采用差压表测量
根据不同高度流体的静压力公式


图4 氨水密度计Fig.4 Ammonia water density meter
测得不同高度的氨水溶液压力差,然后利用式(15)可以求出溶液的密度.该测量方法简单实用、方便快捷,适合一些精度要求不高的场合.
5 结 论
利用Matlab 7.0对4个方程分别计算出它们在每个温度点的饱和液体密度,以及这些计算值与标准值的相对误差,得到结论如下:
a.计算温度-30~55℃的氨饱和液体的密度,Yen-Woods关系式和Campbell改进的Rackett方程计算精度达到要求,其中,后者表现更优越.在整个温度区间,其平均误差为0.38%,最大误差为0.41%,计算精度非常高且稳定.
b.计算温度6~100℃的饱和水的密度,同样,Yen-Woods关系式和Campbell改进的Rackett方程计算精度达到要求,后者的精度更高.在整个温度区间,其平均误差为0.58%,最大误差为1.01%.
c.利用氨水混合溶液的混合性质和超额性质,推导出计算混合溶液密度的公式,同时介绍了氨水溶液密度的实验测量原理,该方法可以验证密度公式的计算精度.
这些研究结果可以用于采用计算机技术对氨水吸收式制冷系统的计算和模拟中,解决了物性计算方面依赖看图查表的困扰.

符号表
[1]Thorin E.Thermophysical properties of ammoniawater mixtures for prediction of heat transfer areas in power cycles[J].International Journal of Thermophysics,2001,22(1):201-214.
[2]Field P E,Combs R J.Aqueous ammonia vapor-liquid equilibrium:entropy and temperature dependence of Wilson coefficients[J].Journal of Solution Chemistry,2002,31(9):719-742.
[3]曾纪珺,杨建明,张伟,等.氨-水体系气液平衡模型的研究[J].化工进展,2010,29(增刊):87-90.
[4]崔晓龙.新型吸收制冷工质相平衡理论与实验研究[D].杭州:浙江大学,2006.
[5]Eubanks L P,Middlecamp C H,Pienta N J.化学与社会[M].段连运,林国强,译.北京:化学工业出版社,2008.
[6]陈新志,蔡振云,胡望明,等.化工热力学[M].3版.北京:化学工业出版社,2009.
[7]Schulz S G C.Equation of state for the system ammoniawater for use with computers[C]//Proceeding of 13th International Congress of Refrigeration.1973:431-436.
[8]沈一忠,冯耀声,侯虞钧.局部组成型M-H(81)状态方程[J].化工学报,1991(5):577-586.
[9]胡望明,侯虞钧.马丁-侯(M-H)状态方程计算二元液液平衡[J].化工学报,1989(1):10-17.
[10]雷群芳,林瑞森,侯虞钧.M-H(81)状态方程与高压液体热导率的计算[J].浙江大学学报(理学版),2003,30(2):173-179.
[11]陈文威,李沪萍.热力学分析与节能[M].北京:科学出版社,1999.
[12]郑丹星.流体与过程热力学[M].北京:化学工业出版社,2010:23-166.
[13]求是科技.MATLAB 7.0从入门到精通[M].北京:人民邮电出版社,2006:24-98.
[14]吴业正,朱瑞琪,李新中,等.制冷与低温技术原理[M].北京:高等教育出版社,2004.
[15]陈新志,侯虞钧.液体混合物密度的关联和预测[J].高校化学工程学报,1995,9(4):383-386.
[16]盘彩美,王文昊,崔晓钰,等.同轴换热器内流动与换热的实验研究[J].上海理工大学学报,2012,34(3):293-297.

