铁磁共振下磁各向异性材料的负折射特性研究

谢桂兵， 耿 滔， 王 燕

（1.上海理工大学 理学院，上海 200093；2.江西师范大学 物理与通信电子学院，南昌 330022）

1968年 Veselago［1］最早对负折射材料 （negative refraction media）进行了探讨.在这种材料中，折射光与入射光居于法线的同侧，电场、磁场和波矢的方向形成左手正交系，因此，又被称为左手材料（left－hand materials）.2000年这一领域受到研究者的关注，Pendry和Smith［2－4］等针对如何实现负折射率材料进行了更详细的探讨，并首次通过实验观察到了微波波段的电磁波通过人工合成介质与空气的交界面时发生的负折射现象.由于负折射材料具有很多奇异特性，如负Cerenkov辐射、反常Dopple效应等，同时它又可用来制作能突破衍射极限的完美透镜（perfect lens）［3］.众多应用前景使得负折射材料的研究成为近年来国际和国内热门的研究领域之一.

如今负折射领域的研究焦点主要集中在负折射材料的寻找与设计上.在过去近十年的研究工作中，研究者提出了各种方案来构造不同的人工合成材料实现负折射，但这些人工合成材料通常只能在某一特定的电磁波频率表现出负折射特性，不具备可调节性.近两年来有研究者提出利用磁性材料构造磁性光子晶体，利用磁性材料的铁磁共振频率随外磁场变化这一特性，通过改变外磁场的强弱来调节磁性光子晶体出现等效负折射率的微波频段［5－7］.但这种磁性光子晶体仍需要构造周期性空间结构，且由于晶格常数与入射波波长相当，因此，不利于负折射材料器件的应用以及微型化.2007年Pimenov等［8］报道了在外磁场条件下，使用天然磁性材料——掺杂型锰钙钛矿 La2／3Ca1／3MnO3的单层膜实现负折射率的研究结果.他们的实验结果表明，此类磁性负折射率材料的工作频段如理论预计的一样，随外磁场的增强而变高.这一研究结果使得磁性负折射材料的制备变得简便且易于应用，同时也具备了工作频段可调节的优点.

掺杂型锰钙钛矿可用分子式R1－xAxMnO3来表示，其中，R 为＋3 价的稀土离子（La，Pr，Nd等），A一般为＋2价的金属离子（Ca，Sr，Ba等），x为二价金属离子的掺杂浓度.这类材料本身是一种特殊的磁性材料，在外磁场下，此类材料的电阻率急剧下降，从绝缘体变为半导体甚至导体，某些材料更是具有高达99.9%的磁电阻，因此，又被称为庞磁电阻（colossal magnetoresistance）材料.由于此类材料在磁记录、磁传感等领域的巨大应用前景，成为近几十年来物理、化学和材料等领域的研究热点之一［9－10］.众所周知，导体的介电常数实部在GHz波段一般都为负［11］.由于庞磁电阻效应，在外磁场下，很多掺杂型锰钙钛矿材料都表现出金属性，介电常数实部为负.同时，磁性材料在发生铁磁共振时会出现负的磁导率实部［12］，这就为负折射率的实现提供了可能.

由于高损耗问题，掺杂型锰钙钛矿的这种新型负折射特性还需要进一步地深入研究.但目前有关掺杂型锰钙钛矿的理论和实验工作主要集中在材料的庞磁电阻效应上，对材料的介电常数和磁导率的频谱研究很少，且都是针对无外磁场时的自然共振的研究，所以，很难用现有的研究成果来指导材料的选取工作.而掺杂型锰钙钛矿材料本身种类繁多，实验研究从1950年开始，至今仍有大量关于新材料特性的报道，所以，完全通过实验一一尝试的方法选材具有较大的盲目性，会耗费大量的人力、物力和时间.因此，本文利用Landau－Lifshitz－Gilbert（LLG）模型理论计算了铁磁共振时材料的磁导率函数和介电函数，研究了等效磁导率和共振频率随外磁场的变化情况，发现通过调节外磁场，能够在很宽广的频率范围内实现负折射.同时还计算分析了此类材料在铁磁共振时的电磁波特性，以期为实验工作提供理论依据.

1 理论计算

当薄膜样品的厚度相对工作波长来说很小，磁化强度矢量运动方程可由LLG模型给出［12］.

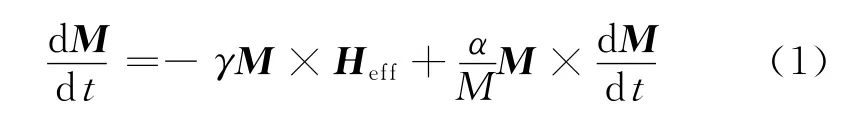
式中，M为磁化强度矢量；Heff为总有效场；t为时间；M为磁化强度；γ为旋磁比；α为阻尼常数.

为了讨论简便，设外恒定磁场H0垂直于薄膜平面，为z轴方向.令磁化强度的自由进动圆频率ω0＝γH0，ωm＝γMs，Ms为材料的饱和磁化强度.则可从方程（1）得到磁导率张量

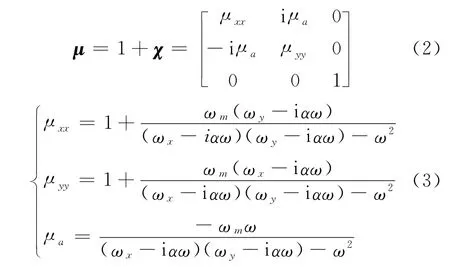
式中，μ为张量磁导率；ω为磁化强度的进动圆频率；μxx，μyy，μa为张量磁导率分量；ωx＝ω0＋（Nx－Nz）ωm，ωy＝ω0＋（Ny－Nz）ωm，分别为x，y方向的共振频率；χ为磁化率张量；Nx，Ny，Nz为归一化退磁因子，对于薄膜材料取Nx＝Nz≈0，Ny＝1；ωr为各磁导率分量的共振频率.

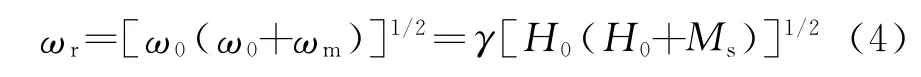
而式（3）可改写为

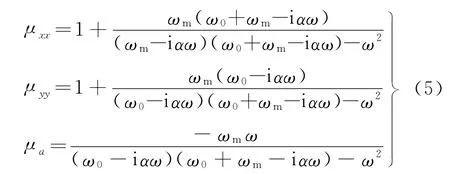
在外磁场条件下，由于巨磁阻效应，掺杂型钙钛矿氧化物材料可以近似认为是金属.当外磁场为μ0H0时，电介质的介电常数是各向异性的［10］.μ0为真空磁导率.此时介电常数张量

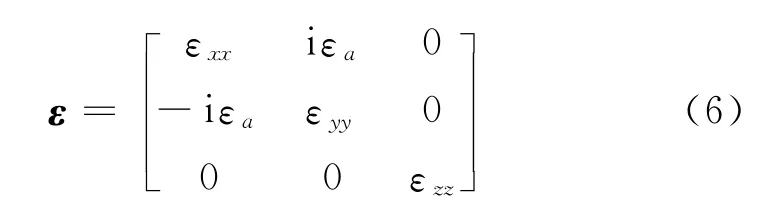
ε的基本参数都与回旋角频率ωc有关.

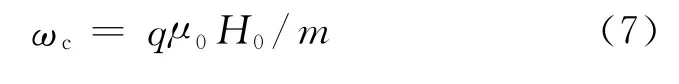
式中，m为带电粒子质量.

在没有电荷和电流分布的均匀介质空间，麦克斯韦方程组表示为

考虑微波波失k沿y方向垂直于薄膜表面入射，设

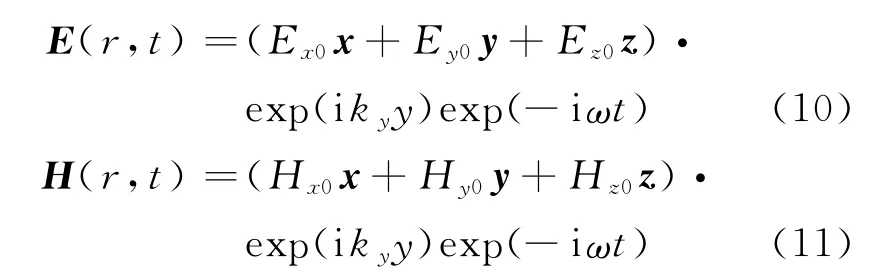
式中，Ex0，Ey0，Ez0为x，y，z方向入射电磁波电场强度；Hx0，Hy0，Hz0为x，y，z方向入射电磁波磁场强度；x，y，z为x，y，z方向单位向量；ky为波矢k沿y方向的分量.

将式（10）和式（11）代入式（8）和式（9），得

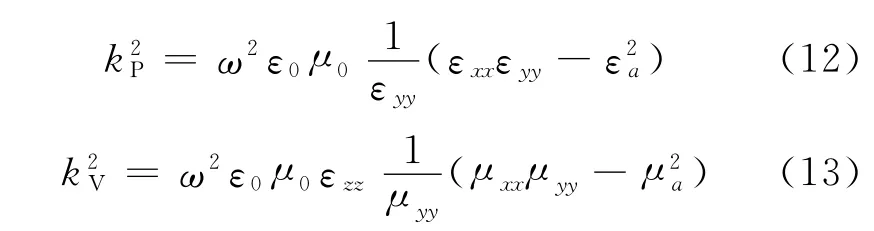
式中，kP为波矢k沿外磁场方向的平行分量，与张量磁导率μ无关，这是因为，此时微波磁场的方向平行于外磁场方向，即沿z轴方向，对磁矩绕外恒定磁场的进动无作用.因此，这种情况下不能发生铁磁共振，不是我们需要的解.kV为波矢k沿外磁场方向的垂直分量，与张量磁导率μ有密切的关系，代表微波磁场的方向垂直于外磁场方向，这种情况能够发生铁磁共振，是需要的解.将kV代回式（8）和式（9）可以分别求得微波电场和微波磁场

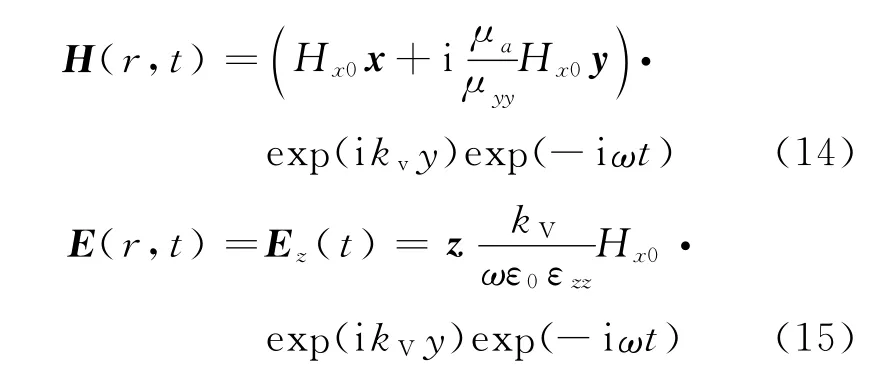
沿波的传播方向仍存在微波磁场的分量，这是由磁导率的各向异性造成的.此时等效介电函数和等效磁导率为

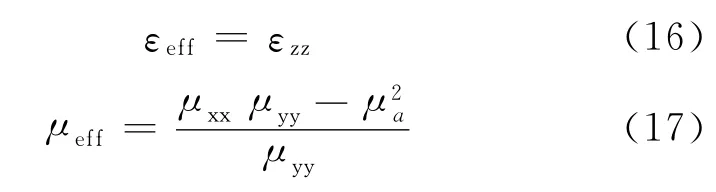
有效介电常数和有效磁导率同时为负的双负材料，其条件为Reεeff＜0且Reμeff＜0.由于微波电场的方向平行于外稳恒磁场，εeff＝εzz，即一般意义上的介电函数不受外磁场的影响.但磁导率的含义已经完全不一样了，此时微波在材料中的传导特性不仅与沿磁场方向的磁导率分量μxx和μyy有关，还受到了分量μa的影响.

2 计算结果及分析

利用式（5）和式（17）可以获得在不同外磁场下的磁导率谱，如图1所示（见下页）.计算时取α＝0.02，根据实验数据［8］，磁化强度M＝4.97×105A／m.对于铁磁材料，一般取朗德因子g＝2，即旋磁比通常作为常量来考虑为电子电量，me为电子质量.在图1中为各磁导率分量的共振频率.铁磁材料的负磁导率主要出现在铁磁共振频率附近.实际上材料体现出来的铁磁共振频率应该是由式（17）表示的等效磁导率的共振频率ωreff，其表达式非常复杂，不同于由式（4）表示的各磁导率分量的共振频率ωr，不利于实际应用.从图1中可以看出，等效共振频率ωreff随着外磁场的增强而增高，略高于ωr，但两者的差别随着外磁场的增强变得越来越小.当μ0H0＝3T时，两者基本相等.因此，在强外磁场的条件下，完全可以用ωr代替ωreff估计材料的工作频率.

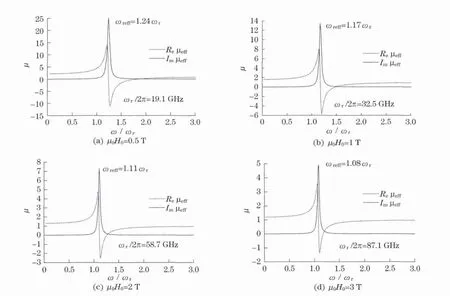
图1 不同外磁场下的等效磁导率谱，α＝0.02，M＝4.97×105 A／mFig.1 Complex permeavility frequency spectra for M＝4.97×105 A／m andα＝0.02 under different external magnetic fields

为了验证这一结论的正确性，用实验数据与理论计算结果进行了比较.根据Pimenov等［8］的实 验结果，在外恒定磁场为5.2T和3.1T时，La2／3Ca1／3MnO3薄膜的铁磁共振频率分别为150GHz和90GHz.此时环境温度为210K，样品的磁化强度约为16（A·m2）／mol［13］.由式（4）计算可知，从理论上来讲，在外恒定磁场为5.2T和3.1T时，磁导率分量的铁磁共振频率ωr分别为141GHz和87GHz，略小于实验结果，误差低于6%.误差原因除了等效共振频率与分量共振频率的固有差别外，还可能来自于两个方面，一是式（4）没有考虑各向异性场Hk的影响，更准确的计算公式应为

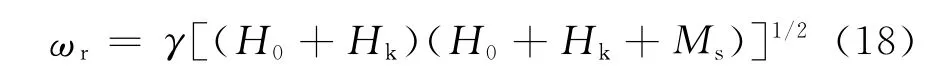
但在强外磁场条件下，一般Hk＜＜H0；二是由于理论计算时将样品薄膜看成二维无限大，实际上薄膜样品是有一定尺寸的，因此，导致了理论计算结果的偏差.但计算结果表明，理论结果已经能很好地反映实验情况.当环境温度升高到270K和295K时，磁化强度减小到约7.5（A·m2）／mol和3（A·m2）／mol［13］.为了在磁化强度改变的情况下不改变铁磁共振频率，理论上，外恒定磁场应该增加到5.33T和5.39T，这与实验结果［8］（约5.30T和5.37T）也符合得非常好.

由式（4）可知，铁磁共振频率可以通过外恒定磁场的大小来调节.根据实验数据，掺杂型锰钙钛矿中Mn离子的每分子磁矩变化范围约在0～4μB之间，μB为波尔磁子，目前超导磁场一般能达到15 T，这意味着在理论上，利用现有的技术，能够在109～1011Hz的广阔频段内调节锰钙钛矿负折射率材料的工作频率，这具有十分诱人的应用前景.

3 结 论

通过铁磁共振条件下张量磁导率的计算，得到了天然磁性薄膜材料锰钙钛矿的负折射特性.发现材料的共振频率随外磁场的增强而升高，表明负折射材料的工作频率受到外磁场的调制.同时强外磁场条件 （μ0H0＞3T）下可以用共振频率ωr替代等效共振频率ωreff，理论结果与实验结果相吻合.

［1］Veselago V G.The electrodynamics of substances with simultaneously negative values of permittivity and permeability［J］.Sov Phys Usp，1968，10（4）：509－514.

［2］Smith D，Willie，Pardlla J，et al.Composite medium with simultaneously negative permeability and permittivity［J］.Phys Rev Lett，2000，84（18）：4184－4187.

［3］Pendry J B.Negative refraction makes a perfect lens［J］.Phys Rev Lett，2000，85（18）：3966－3969.

［4］Shelby R A，Smith D R，Schultz S.Experimental verification of a negative index of refraction［J］.Science，2001，292（5514）：77－79.

［5］Liu S Y，Chen W K，Du J J，et al.Manipulating negative－refractive behavior with a magnetic field［J］.Phys Rev Lett，2008，101（15）：157407－157410.

［6］Zhao H J，Zhou J，Kang L，et al.Tunable twodimensional left－handed material consisting of ferrite rods and metallic wires［J］.Opt Express，2009，17（16）：13373－13380.

［7］Bai Y，Xu F，Qiao L J，The left－handed property of the composite structure of metallic wires［J］.Appl Phys Lett，2009，94（9）：094101－094103.

［8］Pimenov A，Loidl A，Gehrke K，et al.Negative refraction observed in a metallic ferromagnet in the gigahertz frequency range［J］.Phys Rev Lett，2007，98（19）：197401－1974014.

［9］Dagotto E，Hoytta T，Moreo A.Colossal magnetoresistant materials：the key role of phase separation［J］.Phys Rep，2001，344（1／2／3）：1－153.

［10］Salamon M B，Jaime M.The physics of manganites：Structure and transport［J］.Rev Mod Phys，2001，73（3）：583－628.

［11］方容川.固体光谱学［M］.合肥：中国科学技术大学出版社，2001.

［12］戴道生，钱昆明.铁磁学（下）［M］.北京：科学出版社，1998.

［13］Schiffer P，Ramirez A P，Bao W，et al.Low temperature magnetoresistance and the magnetic phase diagram of La1－xCaxMnO3［J］.Phys Rev Lett，1995，75（18）：3336－3339.