基于混合智能算法的电力系统经济调度优化模型研究

宋文宇， 袁光辉， 蒋 艳

（1.三峡大学 电气与新能源学院，宜昌 443002；2，上海理工大学 管理学院，上海 200093）

电力系统调度的中心任务是在保证电网安全、发电量满足需求等因素的情况下，尽可能地使发电费用降低，电力系统调度模型及其算法的研究是一个具有较强应用背景的重要课题.为保证各发电企业公平竞争及实时经济调度，其调度原则、方案应模型化.

电力市场下的经济调度是保证电力市场稳定、有序运行的关键问题之一.经典经济调度是指系统中参加运行的机组已经预先确定的情况下，系统的发电容量大于负荷需求时，将负荷优化分配给各发电机组，达到全系统的燃料消耗量或发电费用最小.采用经济调度方法进行电力调度的确能为电力系统节省很多发电费用，因此经典经济调度得到了广泛的应用.与此同时，各种电力系统调度模型得到了发展，当前各国电力公司采用的实时优化调度程序多数是基于经典经济调度的数学模型，也已经提出了许多优化模型和算法［1－4］.本文提出以煤耗量、污染排放量以及购电费用最小为目标的加权经济调度优化模型，并结合粒子群－人工鱼群算法进行优化计算.实证研究表明：粒子群－人工鱼群算法具有良好的稳定性，其计算结果及收敛性等都比单独使用粒子群算法或人工鱼群算法更优.

1 电力系统网络优化调度模型设计

本文提出以煤耗量、污染排放量以及购电费用最小为目标的加权经济调度优化模型.该模型考虑的约束条件有节点潮流平衡、系统有功平衡、系统正、负备用约束、线路输送容量约束、机组输出功率约束、节点电压约束、机组输出功率上升速率约束、机组最小运行和最小停机时间约束等因素.

已知某电网系统中的发电机组为m台，时段数为T（T的取值一般为24，48，96），G为一个机组24时段发电量的随机向量，PGi（t）为第i号机组在时段t的输出功率（即上网电量）.

1.1 目标函数的确定

a.发电总燃料量目标函数

用f1（G）表示该电网系统发电总燃料量的目标函数，则f1（G）可表示为

式中，ai，bi，ci为表征消耗量曲线特性的常系数.

b.氮氧化物排放量目标函数

用f2（G）表示该电网系统氮氧化物排放量的目标函数，则f2（G）可表示为

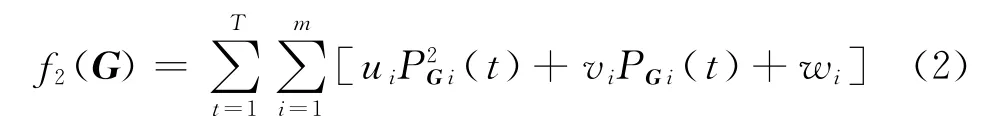
式中，ui，vi，wi为表征此二次曲线特性的常系数.

c.电网购电费用目标函数

用f3（G）表示该电网系统电网购电费用的目标函数，则f3（G）可表示为

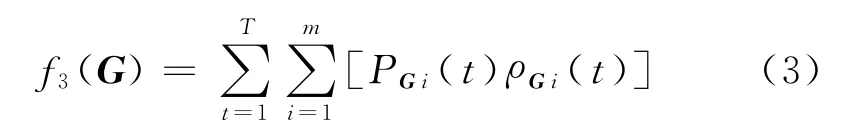
式中，ρGi（t）为各机组在时段t的上网电价，可表示为

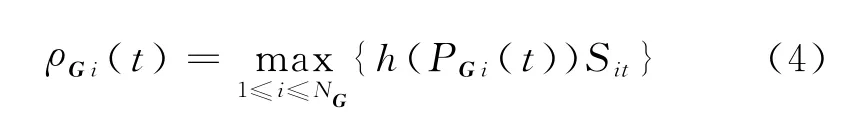
其中，NG为系统注册机组数目，h（PGi（t））为第i台机组t时段的报价函数，Sit为第i台机组t时段的运行标志量，满足

1.2 约束条件的确定

a.系统有功平衡

设Pd（t），Prc（t）分别为时段t时的系统总需求和网络有功总损耗，则系统的有功平衡需满足

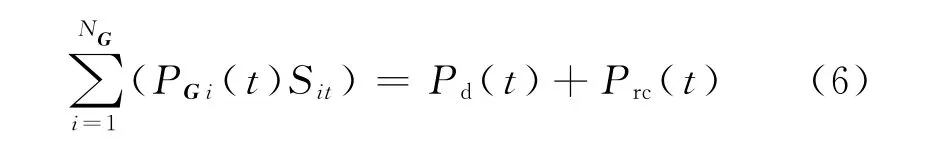
b.系统正、负备用约束

设Pi，max，Pi，min分别为机组i最大、最小输出功率；Rt＋，Rt－分别为系统正、负备用率，则系统的正、负备用需满足

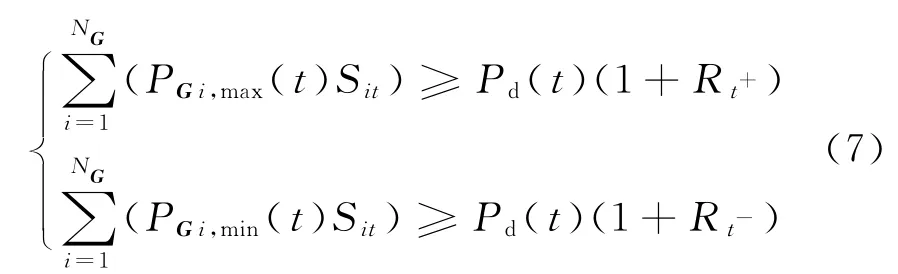
c.机组输出功率约束

对于机组i，其输出功率需满足

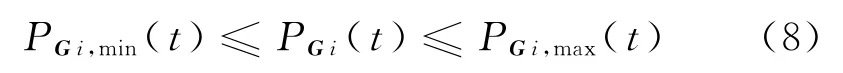
d.机组输出功率上升速率约束

设Di－，Di＋分别为机组i在一个时段内出力的下降、增加幅度，则机组输出功率上升速率需满足

1.3 综合加权优化调度模型

对于第i个目标函数fi（G），设fi，min为第i个目标的最优解，满足fi，min＞0；βi为第i个目标的弹性程度，其弹性区间为（－∞，fi，min＋βifi，min），则目标函数fi（G）的转换函数μ（fi（G））为

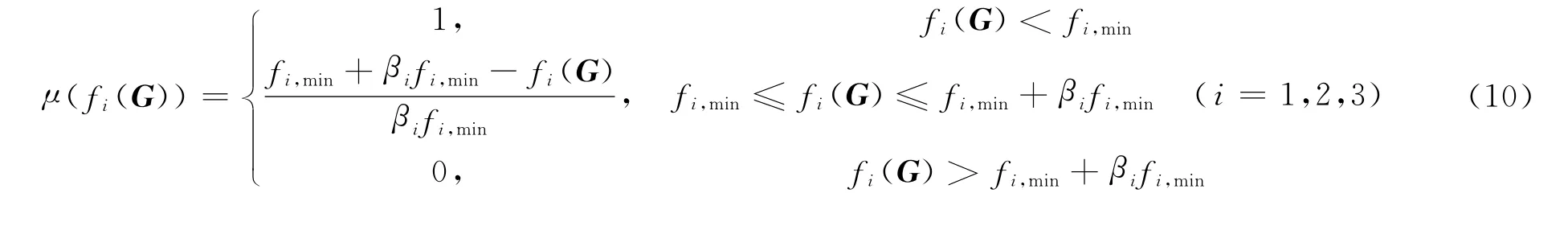
通过该转换函数，电力系统的综合加权优化调度模型可表示为

其中，αi为各目标函数相对重要性的权系数，满足

2 混合智能算法设计

求解电力系统的经济调度问题，计算方法的选取尤为重要.虽然单个的智能优化算法及其改进算法可以解决电力系统调度问题，但不能很好地解决其缺点，为此，很多学者尝试将不同的优化算法相混合［5－8］.

粒子群优化（particle swarm optimization，PSO）算法是Kennedy和Eberhart受人工生命研究结果的启发，通过模拟鸟群觅食过程中的迁徙和群聚行为而提出的一种基于群体智能的全局随机搜索算法，它与其它进化算法一样，是基于“种群”和“进化”的概念，通过个体间的协作与竞争，实现复杂空间最优解的搜索.同时，PSO又不像其它进化算法那样对个体进行交叉、变异、选择等进化算子操作，而是将群体（swarm）中的个体看作是在D维搜索空间中没有质量和体积的粒子（particle），每个粒子以一定的速度在解空间运动，并向自身历史最佳位置和邻域历史最佳位置聚集，实现对候选解的进化.PSO算法具有易理解、参数少、容易实现等优点，对非线性、多峰问题均具有较强的全局搜索能力，在科学研究与工程实践中得到了广泛关注［9－10］.

人工鱼群算法是由李晓磊、邵之江、钱积新等于2002年提出的一种新的群智能优化算法［11］.它采用了自上而下的寻优模式去模仿自然界鱼群的觅食行为，主要利用鱼的觅食、聚群和追尾现象，构造个体的底层行为，通过鱼群中各个体的局部寻优，达到全局最优值在群体中凸现的目的.

人工鱼群算法与粒子群算法都是以研究生物群体行为为基础，主要来源于人工生命和演化计算理论.研究表明：人工鱼群算法具有较好的收敛性，但寻找最优解时，具有较高的时间复杂性，不利于高维数问题的求解；而粒子群算法则通过模拟鸟群集体的协作使群体达到最优，但仅通过更新位置和速度来不断进化到全局最优解，可调参数少，无需梯度信息，因此常造成结果早熟，从而常常无法收敛到全局最优.本文通过将两种算法的结合使用，以获得较高效的且结果优秀的收敛算法.

2.1 算法原理

假设在一个D维的目标搜索空间中，有N个粒子组成一个群落，其中第i个粒子表示为一个D维的向量：Xi＝｛xij｝，i＝1，2，…，D.

第i个粒子的“飞行”速度也是一个D维的向量，记为：Vi＝｛vij｝，i＝1，2，…，N；j＝1，2，…，D.

第i个粒子迄今为止搜索到的最优位置称为个体极值向量，记为：Pbest＝｛pij｝，i＝1，2，…，N；j＝1，2，…，D.

整个粒子群迄今为止搜索到的最优位置为全局极值，为一个D维的全局最优向量，记为：Gbest＝（pg1，pg2，…，pgD）＝｛pgj｝，j＝1，2，…，D.

在找到这全局极值和个体极值时，粒子根据如下的式（12）和式（13）来更新自己的速度和位置，即

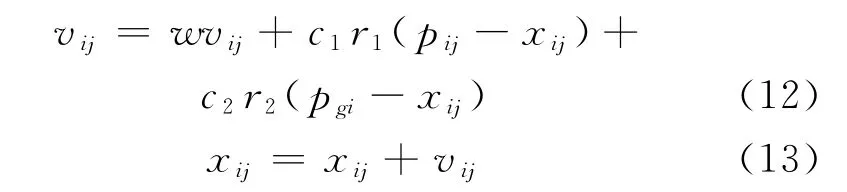
其中，w为惯性系数；c1和c2为学习因子，也称加速常数（acceleration constant）；r1和r2为［0，1］范围内的均匀随机数.根据经验，通常c1＝c2＝2，w在［0.5，1］中取值.i＝1，2，…，D.vid是粒子的速度，设vmax是常数，则vid∈［－vmax，vmax］，由用户设定用来限制粒子的速度.r1和r2是介于［0，1］之间的随机数.

在以上变换完之后，根据AFprey1或AFprey2变换粒子所在位置.变换后速度和位置如式（12）和式（14）所示，即

其中，α和β为位置转换权重（α＋β＝1），使用该权重主要是避免粒子群的早熟或局部最优解.该权重在变化时，α的值为增函数.

2.2 基于混合智能算法的综合加权综合调度模型的算法设计

电力系统调度问题主要是根据约束条件，开始随机生成一群智能粒子，并根据目标函数值对问题进行评价，随后进行智能粒子的值的变更粒子群－人工鱼群算法.对于式（11）所示的综合加权综合调度模型，其算法流程设计如下页图1所示.

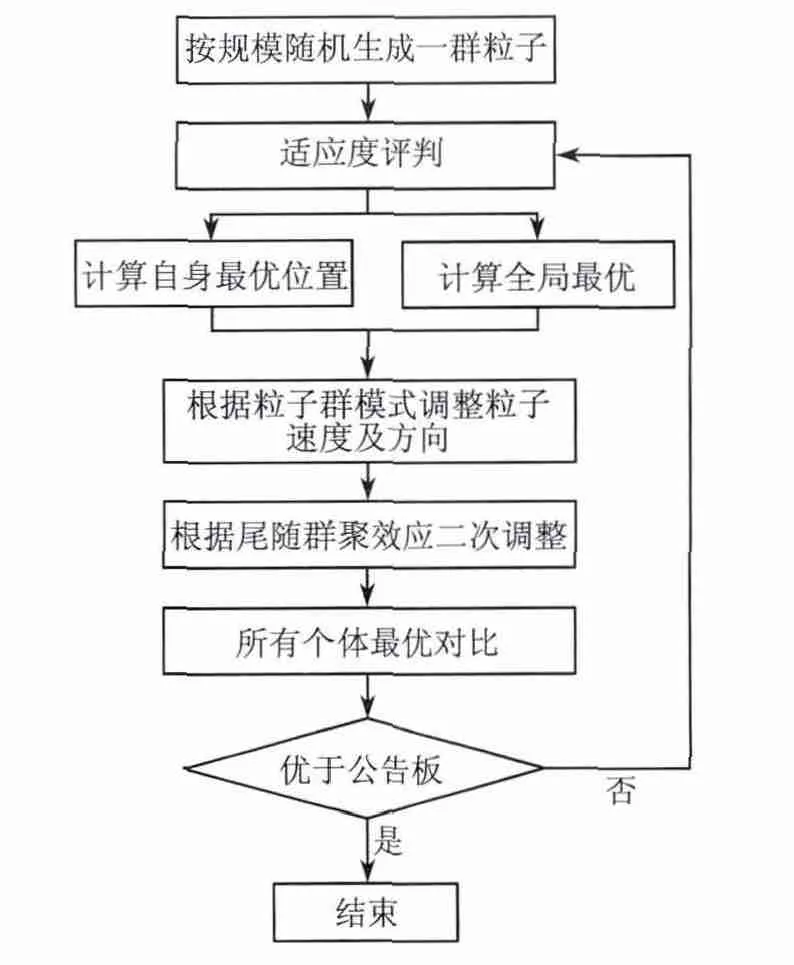
图1 算法流程图Fig.1 Algorithm flowchart

3 基于混合算法的电力系统优化调度模型算例

在针对电力系统调度问题建立动态经济调度模型后，同时针对粒子群和人工鱼群求解该问题的困难所在，提出了粒子群－人工鱼群算法来求解这一问题.通过对综合粒子群算法和人工鱼群算法所得到的混合智能算法进行编程计算，可求解由10个火电竞争商所组成的电力系统调度问题.

采用由10个火电竞争商所组成的电力系统进行调度模拟，在文中求解过程中智能粒子群使用200，50，30的3组种群规模进行计算.初始位置及初始速度随机生成.

对于一个包括10个火电竞争商的电网系统，每一个竞争商等值为一台机组.为简化计算，在一日内各时段采用相同的上网电价，未计及网损，时段数选为24，取β＝0.2.采用本文所述方法，使用种群量为200，50，30的3个种群计算，并对结果进行对比.算例系统参数及各时段的用电需求见表1和表2［12］.

在种群规模为200时，通过粒子群－人工鱼群算法对10个机组，24时段问题进行求解.其中污染量、煤耗量及总购电费用收敛分别如图2所示.

基于种群规模为200，50和30时各项指标计算结果及用时比较见表3和表4.

从计算结果可以看出种群规模越小计算时间越短，但是当种群规模小于20时计算结果的稳定性变差，故该算法的种群规模宜选在25～50之间.通过3种种群规模量的计算结果比较可得：种群规模为50和30的结果优于种群规模为200的情况，且种群规模为50和30时结果的波动不超过10%.故在使用粒子群－人工鱼群算法时，种群规模不宜过大.种群规模为200时计算时间大约为45min；而种群规模为50时计算时间约为11min；种群规模为30时，计算时间约为8min.由此种群规模不宜过大.

表2 24时段需要的负荷量Tab.2 Amount of load required for 24time periods

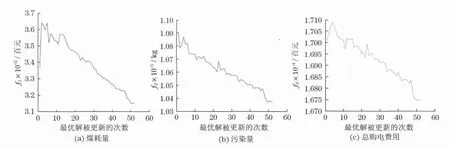
图2 煤耗量、污染量及总购电费用收敛图Fig.2 Coal consumption，convergence figure of pollution and totally cost

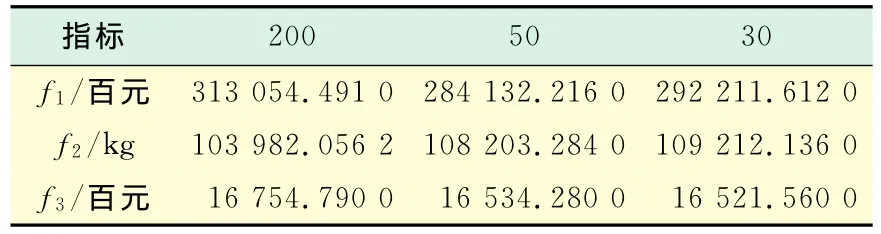
表3 种群规模为不同时的各项指标计算结果比较Tab.3 Results comparison of the indicators for different population size

通过对种群规模为200，50和30的3组结果的对比分析，得到最优调度方案如表5所示.在这组数据求解时，通过粒子群算法求解7次才收敛得到最优解，而人工鱼群算法求解时间更长.应用粒子群－人工鱼群算法进行3次计算，计算结果趋于稳定，其计算结果可信，算法设计合理.

表4 种群规模为200，50，30时种群规模计算耗时比较Tab.4 Calculation time－consuming of population size 200，50，30

表5 在表2负荷情况下最优调度方案Tab.5 Optimal scheduling scheme under load in table 2

4 结 论

针对当前电力市场研究领域中，同时考虑多个目标情况下的不同时段负荷分配问题，提出对各个目标设置不同权重，运用最大满意度的思想来求解多目标经济优化问题.在此基础上，针对当前电力系统调度问题求解较难等提出了粒子群－人工鱼群算法.根据计算结果的比较，发现人工鱼群－粒子群算法在计算时间上有明显优势.多次试验的结果证明了该算法具有良好的收敛性和稳定性.

由人工鱼群－粒子群算法构成的混合智能算法能够大大提高计算效率，对于解决目前在求解最优潮流问题时常常遇到的诸如计算量大、计算速度慢、无法在较短的时间内完成优化计算等问题有很大帮助，故在计算电力系统调度问题中能够得到广泛应用.在实际应用中，可以根据当时当地的情况，动态地调整各个目标对应的权系数，继而动态地分配各机组的出力，已达到利用资源和设备的最佳组合来获得系统最大利润的目的.

［1］吴杰康，唐力.含不确定性负荷的水火电力系统随机优化调度［J］.中国电机工程学报，2012，32（28）：36－42.

［2］张志刚，马光文.基于NSGA－Ⅱ算法的多目标水火电站群优化调度模型研究［J］.水力发电学报，2010，29（1）：213－218.

［3］田廓.基于混沌例子优化－情景约简算法的混合电力系统机组组合模型及其求解［J］.电网技术，2013，37（4）：1020－1024.

［4］温丽丽，刘俊勇.混合系统中长期节能调度发电计划的蒙特卡罗模拟［J］.电力系统保护与控制，2008，36（24）：24－29.

［5］郝玉国，张靖，于尔铿，等.最优潮流实用化研究［J］.中国电机工程学报，1996，16（6）：388－391.

［6］Garnier S，Gautrais J，Theraulaz G.The biological principles of swarm intelligence ［J］.Swarm Intelligence，2007，30（1）：3－31.

［7］马慧民，叶春明，张爽.二进制改进粒子群算法在背包问题中的应用［J］.上海理工大学学报，2006，28（1）：31－34.

［8］马慧民，吴勇，叶春明.车辆路径问题的并行粒子群算法研究［J］.上海理工大学学报，2007，29（5）：435－439.

［9］王万良，唐宇.微粒群算法的研究现状与展望［J］.浙江工业大学学报，2007，35（2）：136－141.

［10］Banks A，Vincent J，Anyakoha C.A review of particle swarm optimization，Part I：background and development［J］.Natural Computing，2007，45（6）：467－484.

［11］李晓磊，邵之江，钱积新.一种基于动物自治体的寻优模式：鱼群算法［J］.系统工程理论与实践，2002，22（11）：32－38.

［12］毛弋，刘文春，张鹏飞.利用模糊算法对电力市场下纯火电系统多目标综合经济负荷进行分配［J］.电力系统及其自动化学报，2000，12（6）：22－29.