窗函数在时空域信号处理中的对比分析

王绪虎，陈建峰，陈万平，张群飞

(1.西北工业大学航海学院，陕西西安710072;2.曲阜师范大学物理工程学院，山东曲阜273165)

加窗在信号频谱分析、随机信号功率谱分析、FIR滤波器设计和波束形成等理论中已被广泛应用。前三者中加窗的本质一致，就是利用窗函数对时域序列进行截短，截短处理也必然会对数据恢复造成不良影响，即产生相应的窗效应［1］。而波束形成可看作一个空域滤波器，对阵列(或天线)接收信号的加权处理可以看作利用一个空间窗函数对空间信号幅值加权，空间窗函数的选取也会对数据处理结果产生影响［2，3］。因此，搞清楚利用窗函数截短数据的影响，掌握加窗原理和选窗原则是非常重要的。本文以矩形(Rectangular)窗、三角(Bartlett)窗，汉宁(Hanning)窗和布拉克曼(Blackman)窗为例，分析它们截短时域和空域信号产生的影响，用对比和类比方法来帮助学生掌握加窗的原理和选窗的原则，根据理论分析设计了相应的实验。

1 窗函数截短时域信号的影响

我们可根据复卷积定理利用窗函数，在时域截短序列转换到频域为

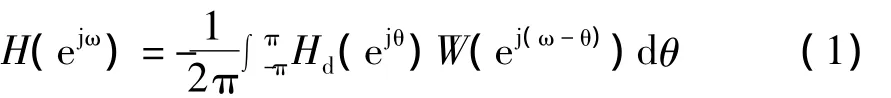
式中Hd表示被截序列的频谱，W表示窗函数频谱，H表示截短序列的频谱。由上式可见，窗函数的频率特性对截短序列的频谱影响很大。若序列具有线性相位，经过简单分析可得其幅度函数为

由上式可得出，截短序列h(n)的幅度谱H(ω)是原序列幅度谱与窗序列幅度谱的卷积。

根据卷积的基本性质可知，窗函数的频谱越接近冲激函数，截短序列的频谱越与原序列的频谱接近。由此可以得出希望选取的窗函数要满足主瓣尽可能窄，最大旁瓣的相对幅度要尽可能小。但这两项要求不可能同时得到满足，因为这两者是相互矛盾的，所以在应用中要根据实际环境要求做选择。

图1和图2分别列出了矩形窗、三角窗、汉宁窗和布拉克曼窗几种常用窗函数的波形和频谱形状。由图可以看出，相同序列长度情况下，窗函数的形状决定其频谱结构。增大序列长度N可以减小窗谱的主瓣宽度，但并不能改变其旁瓣的幅度。以矩形窗为例，增加窗口长度N，则窗的幅频响应在主瓣附近可以写为

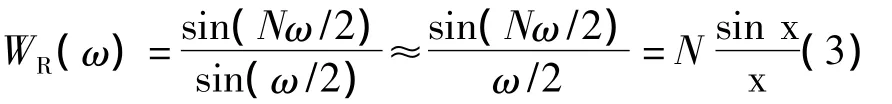
从上式可得出，N比较大的时候，窗的旁瓣幅度与主瓣幅度的比值是不变的［1］。

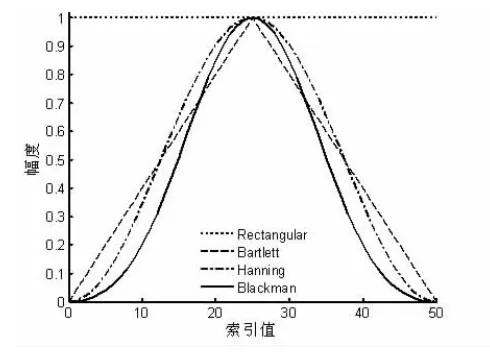
图1 常用窗函数的波形

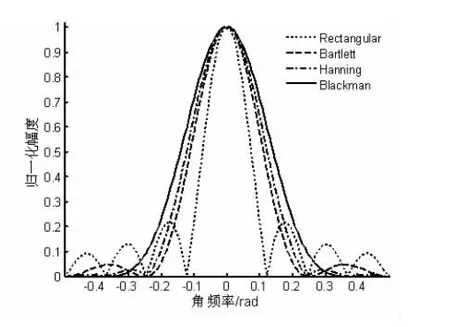
图2 常用窗函数的频谱

2 窗函数对波束形成的影响

波束形成是将阵列各阵元输出经过处理(如加权、延时、求和等)形成空间指向性的过程，可看作一个空间滤波器，滤除空间某些方位的信号，只让指定方位信号通过。假设接收阵列具有M个阵元，阵元以半波长等间距放置，则阵列做波束形成以后的输出可表示为

式中，w=［w1，w2，…，wM］T表示波束形成的加权向量，v=［1，e－jπsinθ，…，e－j(M－1)πsinθ］为阵列的信号流形向量。大多应用场合中，w的元素是一个复数，可以用幅度和相位来表示，其幅度控制波束的形状，相位控制波束的方向。

以空间均匀加权为例来进行分析(即矩形窗加权)。令β=πsinθ，则阵列的方向图为

比较式(5)和式(3)可以看出，两者具有相同的形式。因此，G(θ)中最大旁瓣的相对高度会随着阵元数目增加趋于一个平稳的数值。为了更好地抑制干扰，需要设计出低旁瓣级的波束，均匀加权显然不能满足要求，改变窗函数的形状则是降低旁瓣级的方法之一［4］。

3 仿真实验

实验1：无限长序列hd(n)是截止频率为ωc=0.2π的理想低通滤波器对应的时域序列。利用长度为N=51的窗函数截短无限长序列，分析截短前后频谱的变化及窗函数对截短序列频谱的影响。

利用四种窗函数对hd(n)进行截短，得出长度为N=51的截短序列，对四种序列分别做1024点的离散傅立叶变换，其幅频曲线如图3所示。

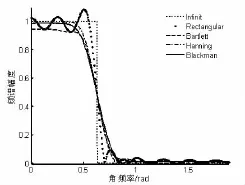
图3 无限长序列截短后的信号频谱

为了比较方便，同时给出了无限长序列的幅频(Infinite)曲线。从图中可看出，无限长序列的频谱中在0.2π处从发生了跳变。利用矩形窗截短的有限长序列频谱在［0，0.18π］和［0.22π，π］内发生振荡，且振荡幅度分别向零和π的方向逐渐减小。在约为0.16π和0.24π位置处振荡幅度最大，过渡带宽度约0.04π。三角窗和汉宁窗截短序列频谱的过渡带基本一致，但三角窗序列频谱在［0，0.15π］平坦段幅度低于汉宁窗截短序列的频谱。这是因为，三角窗在原序列能量比较集中的地方对信号削弱较大造成的。布莱克曼窗截短序列的过渡带最大，但其平坦性最优。通过本实验，形象地展示了不同形状窗函数对截短序列所产生的影响。

实验2：由21个阵元等间距放置的线列阵，分别用四种常用窗函数对其进行幅度加权处理，分析输出波束图的变化。

信号频率为1500Hz，阵元半波长等间距放置(水中声速度设为1500m/s)。分别利用四种窗函数对阵元接收信号进行幅度加权，各种处理方法产生的输出功率的波束图如图4所示。从图中可看出，对应于矩形窗，三角窗、汉宁窗和布拉克曼窗的四个波束，其旁瓣级逐渐减小;三角窗加权波束和汉宁窗加权波束主瓣宽度基本一致;矩形窗加权输出波束主瓣最窄，其次为三角窗加权波束，再次为布拉克曼窗加权波束。这说明窗函数的形状影响输出波束的旁瓣级，但旁瓣级的降低是以扩宽主瓣为代价获得的。图4形象直观地呈现出选用不同的窗函数进行幅度加权，对阵列输出功率波束的影响。

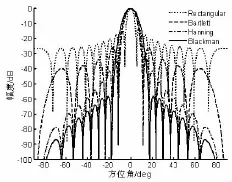
图4 各种权值下阵列的静态波束图

4 数据处理实验

数据处理实验1：测量了两类航行器在良好海况下的辐射噪声数据，利用不同窗函数截取部分数据进行处理，试分析噪声频谱的规律及窗函数对数据频谱的影响。

图5为第一类目标频谱图。从图中可看出，第一类目标的螺旋桨轴频为50Hz，在150Hz和250Hz处明显出现了轴频的3倍和5倍谐波，且幅度依次降低。根据目标的轴频，辅以其它的检测量可用来识别该目标。通过比较可得，利用矩形窗得到频谱图在三个频率上最窄，但在线谱的两侧出现了较高的伪峰，这主要是由窗函数的频谱泄露造成的。可通过选取窗谱旁瓣较低的窗函数来避免此类现象。如图中采用的三角窗、汉宁窗和布拉克曼窗则有效地降低了线谱周围的伪峰。

图5 目标1噪声频谱分析图

图6是第二类目标的频谱图。第二类目标在692Hz、706Hz和711Hz存在三根线谱。从图中可以看出，选用三角窗、汉宁窗和布拉克曼窗适当地抑制掉了线谱周围的毛刺，但其频谱分辨率下降了，如图中706Hz和711Hz处频谱，此时两个频率距离较近，布拉克曼窗已无法将这两个频率分辨开。

图6 目标2辐射频谱分析图

结合上述两类目标的频谱分析可得，选用窗函数要根据具体的应用场合来确定，如果频率差比较大，可选择窗谱旁瓣较小的窗函数，可以抑制频谱的泄露;如果信号频率比较接近，则需选用窗谱较窄的窗函数，来提高频率的分辨率。

数据处理实验2：将六阵元等间距光纤线列阵布放在水下，探测远处的目标，利用四种窗函数对各阵元接收数据进行幅度加权，分析比较输出波束的特点。图7为四种处理方法的输出波束图。

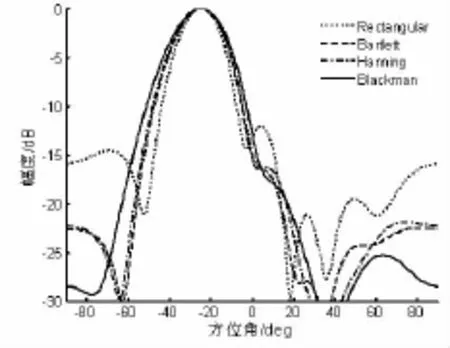
图7 六阵元光纤线列阵波束图

在湖中实验时，船漂浮在水面上，不容易固定，所以不能确定目标的方位，通过波束扫描的方式来获得目标的波束图。通过比较可得，矩形窗、三角窗(汉宁窗和三角窗性能类似)和布拉克曼窗幅度加权的波束旁瓣级依次降低，主瓣宽度依次变宽。因为四种窗其窗谱相对旁瓣级依次降低，因而利用他们进行幅度加权时，输出波束旁瓣级依次降低，但旁瓣级的降低是以扩宽主瓣宽度为代价的，最终输出波束的主瓣宽度依次略有增加。

5 结语

本文分析了加窗对时域和空间阵列信号的影响，并设计了两个仿真实验和两个数据处理实验。通过实验结果，将窗形对截短时域和空域信号的影响形象直观地呈现给学生，让学生在对比和类比分析中理解用窗函数截短数据的影响，掌握利用窗函数截取数据的原理和选择窗函数的原则。课程设计既注重了理论分析和数值实验，又坚持了基础理论内容与科学研究内容的结合，体现了探究性学习的基本思想。教学实践证明，该课程设计锻炼培养了学生科研思维和科研方法，提高了学生综合运用知识的能力，教学效果良好。

［1］程佩青.数字信号处理教程(第二版)［M］.北京：清华大学出版社，2001.

［2］田坦，刘国枝，孙大军.声呐技术［M］.哈尔滨：哈尔滨工程大学出版社，2000.

［3］李志舜.鱼雷自导信号与信息处理［M］.西北工业大学出版社，2003.

［4］Van Trees，H.L.著.汤俊，等译.最优阵列处理技术［M］.北京：清华大学出版社，2008.