广域监视动目标检测模式下动目标快速定位误差分析

郑世超 宋红军 刘亚波 闫 贺② 吴 琨②

①(中国科学院电子学研究所 北京 100190)

②(中国科学院大学 北京 100039)

1 引言

广域监视(Wide Area Surveillance,WAS)雷达在载机飞行过程中，波束在方位向快速重复扫描，完成对热点区域动态监视。广域监视模式具有监视区域广、重访率高、可跟踪目标动态、识别目标特征和类别等优势，在机载雷达系统中受到了广泛地重视[1]。该模式在军事上已经得到了成功应用：美国在伊拉克战争期间利用 E-8 JSTARS上的 WASGMTI (Wide Area Surveillance-Ground Moving Target Indication)模式在夜间成功侦察到伊拉克装甲兵部队的撤退行动；而该模式在民用方面的探索也已经开始[2]：德国的PARMIR系统可以通过WASGMTI模式实现交通监管[1]。

WAS-GMTI模式通过快速扫描，实现大面积区域内的动目标监视；通过连续扫描，实现对热点地区的重复监测，获取同一动目标的多次信息，以确定动目标的运动轨迹。因此，这种模式下动目标的数据量非常大，而从战场或者交通监测的需求出发，都需要对动目标的处理尽可能实时地进行，这就要求对动目标进行快速的定位。星载SAR中使用雷达回波的距离多普勒参数对目标进行定位的方法需要联合距离方程、多普勒频率方程和地球模型方程进行求解[3]，过程较为复杂。而机载情况下可以忽略地球曲率的影响，只需要联合前两个方程求解[4]。但是在机载 WAS-GMTI模式下，对动目标进行定位时动目标相对载机的斜距和斜平面方位角是已知的，因此只需要考虑根据斜距和斜平面方位角解算动目标经纬度的问题，动目标定位的问题从而得到相应的简化。在实际工程实现中，动目标的定位受到诸多因素的影响，直接使用理想公式对动目标进行定位存在较大误差。本文对实际中存在的这些导致动目标定位误差的因素的影响进行了分析，在动目标定位时考虑这些因素的影响，就可以实现对动目标更加准确的定位。

本文的结构安排如下：第 2节对 WAS-GMTI模式做简要的介绍，给出本文采用的广域监视动目标检测模式下的动目标快速定位方法；第3节详细分析了导致动目标定位产生误差的诸多因素的影响；第4节使用仿真和实测数据中的动目标信息结合本文分析完成了动目标定位，定位结果验证了本文对动目标定位误差的分析的合理性。

2 动目标定位

WAS-GMTI模式是一种在大面积区域内实现快速监视地面运动目标的工作方式。WAS-GMTI模式下的距离向覆盖范围和距离向分辨率与常规条带模式SAR相同；而在方位向上，由于其天线采用方位向扫描的工作方式，方位向覆盖范围和方位向分辨率具有新的特点。对于WAS-GMTI系统来说，其覆盖范围包括载机在一次扫描时间内飞行飞过的距离和天线方位向扫描所扩大的测绘范围。因此在这种模式下，相同飞行时间内可以获得更大范围区域的信息[5－7]。

在广域监视动目标检测模式下，可以获得的动目标的信息包括载机到动目标的斜距和动目标的方位角。其中斜距通过回波时延来计算，而动目标的方位角在这里被定义为动目标和载机连线与载机机头方向的夹角。

从实际工程中的实时性要求出发，本文采用了一种快速的动目标定位方法：首先根据动目标的斜距和方位角信息，求出动目标与载机在地面的投影之间的地距OP和OP相对于正侧视方向的方位角φ1。根据图1中的几何关系(图中，OCD所在平面是零多普勒面)，可以求得 φ1=arcsin(X/r)，其中X=R⋅si n(9 0−θ),θ为动目标与载机的连线和载机机头方向的夹角。

图2 动目标定位几何关系(右侧视)Fig.2 Moving target location geometry (right side-looking)

如图2所示，在获得了动目标与载机在地面的投影之间的地距OP和OP相对于正侧视方向的方位角φ1之后，就可以根据几何关系得到动目标与载机在地面的投影之间的相对方位角，则动目标的定位问题就转换为已知一点经纬度和两点之间的相对方位角，求解另一点经纬度的问题。

根据载机和动目标之间的位置关系，可以分为右侧视和左侧视两种情况对动目标进行定位。将图2中的几何关系联系距离经纬度转换公式可以得到动目标所在位置的经纬度的计算公式。

如图2所示，在右侧视情况，P点经纬度可以表示为：

其中，Δs表示同一经线上纬度相差1o的间隔长度，为Re⋅(π/180°)(Re为地球半径 6371.004 km); φ2是载机的航迹角，用载机飞行方向和正北方向之间的夹角来表示。

同样，在左侧视情况下，P点经纬度可以表示为：

通过式(1)或者式(2)，就可以计算得到动目标所在位置的经纬度，从而完成了对动目标的定位。

3 WAS-GMTI动目标定位误差分析

在 WAS模式下，通过杂波抑制、动目标检测和动目标参数估计后得到动目标的相关信息，最终使用其方位角和斜距对动目标进行定位。其中斜距误差由系统时间延迟引起，文献[4,8]中具体分析了其对SAR图像定位的影响。考虑到WAS模式下的动目标定位中斜距误差的影响和普通 SAR图像定位中类似，所以本文对此不再做具体分析。

3.1 载机姿态误差对动目标方位角的影响

因为解算得到的动目标的方位角是相对于天线排列方向的，在实际工程中天线一般沿载机机身方向排列，即动目标方位角是相对于机身方向的。而对动目标进行定位时，使用的是相对于载机飞行方向的方位角，我们称之为理想的动目标方位角。所以，如果载机姿态存在误差，机身方向与载机飞行方向不同，就会导致解算出的动目标的方位角与理想的动目标方位角间存在误差，最终导致动目标的定位误差。

载机姿态误差中，对动目标方位角产生影响的主要是偏流角和俯仰角，下面对这两种因素对动目标方位角的影响进行分析。

3.1.1 偏流角对动目标方位角的影响

如图3所示，偏流角是指载机飞行方向和机身方向在水平面内的夹角。在分析偏流角对动目标方位角的影响时，假设其它参数都是准确的。

解算得到的动目标的方位角是相对于天线方向的(即机身方向)，在理想情况下航迹方向和机身方向相同，可以直接使用解算得到的动目标方位角进行定位。但在实际工程中，偏流角的存在导致航迹方向和机身方向在水平面内存在误差，直接使用解算得到的动目标方位角进行定位会产生定位误差。

如图3所示，解算得到的动目标的方位角为角β，而要想对动目标进行准确的定位，需要使用理想的动目标方位角α。偏流角引起的角α和角β之差将导致动目标定位的误差，下面具体分析偏流角对动目标方位角的影响。

首先将角β投影到地平面上得到角β1，从P点向机身方向所在直线作垂线，则该垂点在地面的投影与P点的连线垂直于机身方向所在直线在地面的投影。可以得到 cos β=X/ R,c os β1=X/ r=(R/ r)⋅cosβ，所以

则角β1和角α在地平面的投影角α1的关系为：

从而求得动目标定位中需要的理想的动目标方位角为：

可以发现，由于载机偏流角的存在，导致动目标定位中需要的理想的动目标方位角与解算得到的动目标方位角之间存在误差，从而使得最终的动目标定位产生误差。为了对动目标进行更准确的定位，要在定位之前根据载机的偏流角和解算得到的动目标方位角计算出理想的动目标方位角。

3.1.2 俯仰角对动目标方位角的影响

如图4所示，俯仰角定义为载机飞行方向和机身方向在垂直平面内的夹角。同样的，在分析俯仰角对动目标定位的影响时，忽略其它影响动目标定位的因素，与对偏流角对动目标定位的影响的分析类似。

将解算得到的方位角β投影到航迹所在的垂直平面上得到角β2，从P点向机身方向所在直线作垂线，则该垂点与P0点的连线垂直于机身方向所在直线。可以得到 cos β=X/ R,c os β2=X/ Rh=(R/ Rh)⋅cosβ，所以：

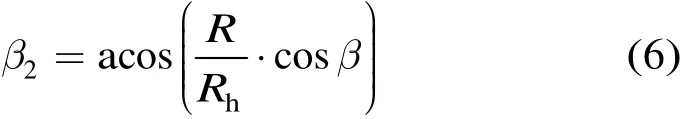
则角β2和理想的动目标方位角α在地平面的投影角α2的关系为：

从而求得动目标定位中需要的理想的动目标方位角为：

同样可以发现，在实际工程中，俯仰角的存在导致航迹方向和机身方向在垂直面内存在误差，从而导致动目标定位中需要的理想的动目标方位角与解算得到的动目标方位角之间存在误差，从而使得最终的动目标定位产生误差。为了对动目标进行更准确的定位，要在定位之前根据载机的俯仰角和解算得到的动目标方位角计算出理想的动目标方位角。

3.2 斜距转换为地距的误差对动目标定位的影响

对动目标进行定位时用到的是载机在地面的投影和动目标之间的地距，而我们获得的是载机到动目标之间的斜距，所以在定位之前要将斜距转换为地距。实际工程中斜距转换地距时一般使用的都是直角模型，这将导致计算得到的地距存在误差，最终影响动目标的定位。为了提高动目标定位的精度，可以在斜距转换地距时使用球体模型。下面对两种模型下斜距转换地距的区别进行分析。

直角模型下斜距转换地距的公式为：

其中h为飞机和目标所在区域之间的相对高度。

地球球体模型下地距可以通过式(10)计算得到：

其中Re为动目标所在区域的地球半径。

为了分析两种模型下，斜距转换地距的差异，我们对此进行了仿真。设定h从3 km到18 km，R从30 km到180 km，直角模型和地球模型下计算得到的地距之差如图5所示。

可以发现，随着斜距、相对高度的增大，两种模型下计算得到的地距之差随之增大。但是地距之差的绝对值较小，在实际应用中这两种模型之间的差别对最终定位的影响较小。

载机的飞行高度误差和动目标所在区域的高程误差都会导致斜距转换地距时误差的产生，而这两者的影响可以综合为载机和动目标所在区域之间相对高度的影响。下面分别分析直角模型和地球球体模型下，相对高度误差和斜距误差对地距的影响。

直角模型下相对高度误差和斜距误差导致的地距误差为：

其中h是平台和目标之间的相对高度，R是平台与目标之间的斜距。

而在地球球体模型下相对高度误差和斜距误差导致的地距误差为：

Re为动目标所在区域的地球半径。

3.3 地距、平面方位角误差对动目标定位的影响

在将斜距和动目标方位角分别转换为地距和平面方位角之后，动目标的定位问题就转换为已知一点经纬度和两点之间的相对方位角，求解另一点经纬度的问题。从经纬度计算公式中可以发现，对经纬度最终计算结果产生直接影响的是两点之间地平面内的相对方位角和地距。所以下面对这两个直接因素进行分析，它们对定位的影响为：

其中，φ=(lat1+lat2)/2是载机在地平面的投影和动目标的平均纬度，γ是它们之间的相对方位角。根据侧视方向不同，γ有不同的表达式，分别为γ=φ2−90−φ1(右侧视)，180−φ2−φ1(左侧视)。

我们对方位角和地距对最终的经纬度计算的结果分别进行仿真分析，设定地距r从30 km到180 km，相对方位角为0°到180°。

图6、图7给出了单位(1 km)地距误差导致的经纬度计算结果的误差。

可以发现：随着动目标所处区域纬度的增大，单位地距误差导致的经度计算误差迅速增大。

图6 不同纬度、不同方位角单位地距误差导致的纬度计算误差Fig.6 Latitude calculation error of different angles and different latitudes by unit range error

图7 不同纬度、不同方位角单位地距误差导致的经度计算误差 Fig.7 Longitude calculation error of different angles and different latitudes by unit range error

图8 不同方位角、不同地距单位相对方位角误差对纬度计算的影响Fig.8 Latitude calculation error of different angles and different ranges by unit angle error

图9 不同方位角、不同地距单位相对方位角误差对经度计算的影响 Fig.9 Longitude calculation error of different angles and different ranges by unit angle errorror

图8、图 9给出了单位相对方位角误差导致的计算结果的误差，在这里我们设定了两点之间的平均纬度为40°(平均纬度对纬度的计算没有影响；对经度的计算有一定影响，表现为：随着动目标所在区域纬度的增大，单位方位角误差导致的经度计算误差缓慢增大)。

3.4 地距经纬度转换模型对动目标定位的影响

动目标的定位最终归结为，已知地球上一点的经纬度以及两点之间的相对角度和距离求解另一点的经纬度的问题。而前面的距离经纬度转换都是在正球体模型下进行的，正球体模型下的距离经纬度转换会存在一定的误差[9]。如果需要减小这一误差，可以使用椭球体模型下的距离经纬度转换公式。

表1对椭球体模型和正球体模型下经纬度计算误差进行对比分析(其中椭球体模型使用的是克拉索夫斯基椭球，解算时使用了贝塞尔大地主题解算方法)。

表1 正球体模型和椭球体模型下距离转换经纬度结果对比Tab.1 The conversion result contrast of orthogonal model and sphere model

可以发现，相对于正球体模型，椭球体模型下的经纬度解算精度得到了很大提升。而且随着两点之间距离的增大，椭球体模型的优势愈发明显。

3.5 平台测量误差对动目标定位的影响

载机平台位置对动目标定位的影响主要体现在载机平台经纬度和高度上，平台的高度误差可以整合到相对高度误差中进行分析；而平台经纬度对WAS模式下动目标定位的影响较为简单且与对普通SAR图像定位的影响类似[8]，所以本文对此不再做具体分析。

4 动目标定位验证

为了验证本文对 WAS模式下影响动目标定位的诸多因素(不包括椭球体模型和正球体模型的差别)的分析，我们对比仿真了直接按照理想公式进行定位的结果和考虑这些因素后重新定位的结果。系统的仿真参数见表2所示，其中载机飞行方向以正北为0°，顺时针递增。

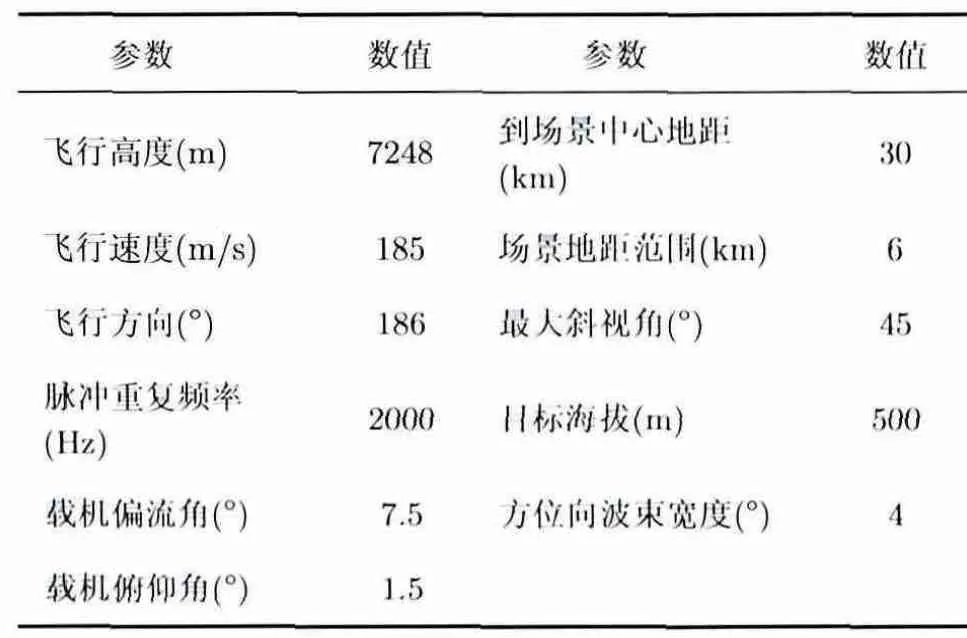
表2 仿真参数Tab.2 Simulation parameters

从前面的分析可以发现，载机的姿态、斜距转换地距时使用的模型等因素会给动目标的定位引入误差。使用读取得到的载机姿态误差和解算得到的动目标方位角，根据式(7)和式(8)就可以计算得到定位时需要的理想的动目标方位角，从而减小了载机姿态误差对动目标定位的影响。另外，在将载机和动目标之间的斜距转换为地距时，使用地球球体模型替代直角模型也可以提高动目标定位的精度。我们随机选取了6个动目标，对仿真时设定的动目标经纬度和定位结果进行对比，分析其误差如表3所示。

为了进一步确定误差分析的可靠性，我们使用蒙特卡洛实验对分析结果进行验证。在实际飞行中，飞机的姿态误差是变化的，因此在本实验中我们设定飞机的偏流角作为随机变化量(偏流角变化范围在正负7.5°之间)，其它参数不变，在此基础上进行1000次蒙特卡洛实验的结果如图10所示。

表3 设定的动目标经纬度和定位结果的对比Tab.3 Contrast between location results and original coordinates

图10 使用理想公式和考虑偏流角影响重新定位的定位误差对比Fig.10 Error contrast between direct location and relocation

通过上面的仿真实验可以发现，与直接使用理想公式进行定位相比，考虑了载机姿态误差等因素之后对动目标重新定位的误差显著减小。

同样，我们使用实测数据对考虑本文分析的因素后的定位结果进行了验证，实际系统的参数如表4所示。实测数据中对应场景为内蒙古某市的德萨线公路附近，经纬度范围为：东经110.453°～110.543°，北纬40.192°～ 40.273°。

使用理想公式直接定位的结果如图11所示。

表4 实测数据系统参数Tab.4 System parameters of real data

可以发现，动目标定位的位置距离地图中的主要道路较远，定位结果存在较大误差。使用计算得到的理想的动目标方位角并根据地球球体模型进行斜距地距转换之后，重新定位的结果如图12所示。

可以发现，重新定位之后运动目标都被标注到了相应区域的道路附近，定位的精度得到提升。图中不同颜色的点代表不同速度的动目标，如果动目标估计得到的参数是正确的，重新定位之后这些动目标就能被准确地标注到道路上。但是由于实际数据处理过程中受到噪声的影响，而且两通道系统解算得到的动目标速度本身存在模糊，从而导致估计得到的动目标的参数可能存在误差，使得部分目标不能准确定位到道路上。尽管如此，重新定位之后定位结果的改善仍充分验证了本文对导致动目标定位误差的影响因素的分析的合理性。

5 结论

根据机载广域监视动目标检测模式下可以获得的动目标信息的特点，本文采用了一种快速定位方法实现动目标的定位。在实际工程中，动目标的定位受到诸多因素的影响，直接使用理想公式对动目标进行定位存在较大误差。文章对实际中存在的这些因素对动目标定位的影响进行了分析，并在考虑这些因素之后对动目标进行了重新定位。通过仿真实验和实测数据验证了本文所提出的动目标快速定位方法的有效性和对动目标定位误差的分析的合理性。

[1]Brenner A R,Ender J H G,et al..Demonstration of advanced reconnaissance techniques with the airborne SAR/GMTI sensor PAMIR[J].IEE Proceedings-Radar,Sonar and Navigation,2006,153(2): 152-162.

[2]Entzminger J N,Fowler C A,Kenneally W J,et al..JointSTARS and GMTI: past,present and future[J].IEEE Transactions on Aerospace and Electronic Systems,1999,35(2): 748-761.

[3]袁孝康.星载合成孔径雷达目标定位研究[J].上海航天,2002,1(1): 1-7.Yuan Xiao-kang.Studies of ground target location of spaceborne SAR[J].Aerospace Shanghai,2002,1(1): 1-7.

[4]彭代强,林幼权,杜鹏飞.机载 SAR 图像快速经纬度计算及精度分析[J].现代雷达,2010,32(3): 48-52.Peng Dai-qiang,Lin You-quan,and Du Peng-fei.A fast algorithm for latitude and longitude calculation for airborne SAR and its location precision analysis[J].Modern Radar,2010,32(3): 48-52.

[5]郑明洁,闫贺,张冰尘,等.基于DBS图像的双通道广域监视雷达动目标检测和参数估计方法[J].雷达学报,2012,1(1):36-42.Zheng Ming-jie,Yan He,Zhang Bing-chen,et al..A novel method of moving target detection and parameters estimation for Bi-Channel WAS radar based on DBS image[J].Journal of Radars,2012,1(1): 36-42.

[6]Yan He,Wang Robert,Li Fei,et al..Ground moving target extraction in a multichannel wide-area surveillance SAR/GMTI system via the relaxed PCP[J].IEEE Geoscience andRemote Sensing Letters,2013,10(3): 617-621.

[7]Yan He,Li Fei,Wang Robert,et al..Moving targets extraction in multichannel wide-area surveillance system by exploiting sparse phase matrix[J].IET Radar,Sonar &Navigation,2012,6(9): 913-920.

[8]高祥武,黄广民,杨汝良.机载 SAR 目标快速定位方法和定位精度分析[J].现代雷达,2004,26(9): 4-7.Gao Xiang-wu,Huang Guang-min,and Yang Ru-liang.Study on a fast target location method for airborne SAR and location precision analysis[J].Modern Radar,2004,26(9):4-7.

[9]卫宇.考虑地球曲率情况下两点距离问题的求解[J].航空兵器,2008,(3): 7-12.Wei Yu.Solution of distance between two points considering curvature of the earth[J].Area Weaponry,2008,(3): 7-12.