基于广义MUSIC算法的低仰角估计新方法

蒋柏峰 吕晓德 向茂生

①(中国科学院电子学研究所微波成像技术国家级重点实验室 北京 100190)

②(中国科学院大学 北京 100049)

1 引言

由于工作在 VHF频段的雷达具有良好的反隐身、反辐射导弹性能，近年来重新受到业界的重视。对于低仰角目标，当雷达俯仰向波束较宽时，目标的直达波信号和经反射面反射产生的多径信号都将位于接收天线的主瓣范围之内。由于直达波与多径信号的波程差较小，二者之间只存在复反射系数及微小的时延差异，因此二者具有较强的相关性。这造成俯仰向波瓣分裂，对低仰角目标的 DOA估计与跟踪产生严重影响[1－12]。针对这一问题，文献[2,3]提出一种利用波瓣分裂的仰角测量方法，该方法利用多径反射模型，分析波瓣分裂情况，进而利用单脉冲测角方法实现角度测量。这种方法虽然结构简单，计算量较小，但是严重依赖反射系数，在反射模型不准确时，性能严重下降。多径情况下的DOA估计问题，本质上是相干信源情况下的 DOA估计问题。在空间谱估计领域，利用空间平滑、最大似然等方法可以实现相干信源角度估计，但存在阵列自由度损失、计算量大等问题[4－6]。文献[7]提出了广义 MUSIC算法，该算法可直接应用于相干信源DOA估计。文献[8]在广义MUSIC算法基础上，提出了一种新的谱峰搜索方法，该文利用目标距离信息将2维角度搜索转化为1维搜索，降低了运算量。文献[9]在文献[8]基础上提出一种多径衰减系数和仰角联合估计的算法。

针对多径情况下的低仰角目标DOA估计问题，本文首先介绍了广义MUSIC算法及两种改进算法，理论分析指出这些算法有效性的实质是对基本谱峰搜索公式的加权。权值的不同导致了角度估计性能的差异。在此基础上，本文分析了权值及目标角度位置对 DOA估计结果的影响，提出了基于广义MUSIC算法的低仰角估计方法模型。通过仿真试验，本文确定了一个性能较为优异的权值。仿真试验表明，基于该权值的算法相比已有算法具有更高的估计成功概率，更优的估计性能。

2 广义MUSIC算法及其改进算法

多径信号由镜面反射分量和漫反射分量组成，当反射面较为平坦时，可以忽略漫反射分量，只考虑镜面反射分量的影响[12]。此时阵列接收信号可表示为[9]：

阵列接收信号的协方差矩阵可表示为[13]：

式中σ2为噪声功率，US为M×1维信号子空间，UN为 M×(M−1)维噪声子空间，“H”表示共轭转置。

由阵列流型与噪声子空间的正交性可得：

利用式(3)进行DOA估计时，涉及θd,θs,3 个变量的搜索，运算量非常大。针对这一问题，文献[7]提出的广义 MUSIC 算法，去除了对谱峰搜索的影响，其谱峰搜索公式为：

由广义Rayleigh商的性质，式(4)可以等效为：

θd和θs之间的关系可表示为：

式中h表示天线的高度，Rd表示目标到天线的距离。

文献[9]在文献[8]基础上提出了多径衰减系数与角度的联合估计方法，可表示为：

式中ω=[1 0]T。

3 算法的理论分析

3.1 已有算法的理论分析

常规MUSIC算法的谱峰搜索公式可表示为[13]：

对于常规 MUSIC算法来说，式(9)与式(10)没有本质区别，利用二者得到的DOA估计结果也是相同的。对于广义 MUSIC算法及改进算法来说，也存在类似的两种形式的谱峰搜索公式，前文介绍的 3种算法使用了式(10)形式的谱峰搜索公式。这两种形式对于广义MUSIC算法及改进算法来说，差异是巨大的。下面将通过理论分析说明这一问题。

令

3种算法式(10)形式的谱峰搜索公式可表示为：

其中，“*”表示复数共轭。3种算法式(9)形式的谱峰搜索公式可表示为：

由上述公式可知，3种算法的谱峰搜索公式分母都为 A11A22−A12A21，只是分子有所不同。理想情况下，当角度取 θd,θs时，A11A22−A12A21=0，此时将形成尖锐的谱峰，因此可利用上述公式进行谱峰搜索。需要注意的是，当角度取值接近 0°，即θd≈θs≈0°时，A22A11−A21A12≈0。此时3种算法式(9)形式的谱峰搜索将得到很大的谱值。在实际情况下，目标角度处的谱值是有限的，0°附近的大谱值将淹没目标角度处的谱值，此时将严重影响目标的 DOA估计。3种算法式(9)形式的谱峰搜索公式在实际应用中性能很差。

考察3种算法式(10)形式的谱峰搜索公式可知，当角度取接近0°值时，谱峰搜索公式的分子也接近0，这相当于对式(9)形式的谱峰搜索公式进行了加权，抑制了小角度产生的大谱值。可以预见，相比式(9)形式的谱峰搜索公式，式(10)形式的谱峰搜索公式在低信噪比时将更为有效。而这种有效性的本质是通过加权，抑制了小角度产生的大谱值。已有的3种算法正是使用了式(10)形式的谱峰搜索公式。

3.2 基于广义MUSIC算法的仰角估计方法模型

由前文的分析可知，广义 MUSIC算法及改进算法有效性的实质是对基本谱峰搜索公式(A11A22−A12A21)−1的加权。这就是基于广义MUSIC算法的仰角估计方法模型。权值不同，仰角估计性能也不尽相同。因此权值是影响算法估计性能的关键。

加权的目的是抑制小角度产生的大谱值。从已有3种算法的权值来看，可以认为权值是以A11,A12,A21,A22,a12,a21为变量的函数。该函数要求角度取值接近0°时函数值接近0。变量 A11,A12,A21,A22不仅与角度有关，还与噪声子空间有关，利用这些变量构造的权值具有一定的随机性，加权效果难于控制和分析。因此本文主要分析以 a12,a21为变量的权值。具体来说是要构建权值函数 f(a12,a21)，使得该函数在角度取值接近 0°时函数值接近 0。比较直观的两种构造方式为：

式(17)，式(18)中m为可变的加权系数。

角度取值接近 0°时，式(17)，式(18)的取值接近0。加权系数m影响权值接近0的速度，进而影响加权效果，最终对 DOA估计结果产生影响。合理的m取值可以通过仿真试验得到。由前文分析可知，式(9)形式的谱峰搜索公式DOA估计效果较差，主要是受小角度产生的大谱值影响。因此可以预见，目标角度越接近0°，这种影响越大，DOA估计性能越差。信噪比是影响DOA估计的另一个重要因素，信噪比越低，DOA估计性能越差。因此在分析不同权值对 DOA估计的影响时，要综合考虑目标角度及信噪比两方面因素的影响。

4 算法仿真及性能分析

本节将首先通过仿真试验说明权值对广义MUSIC算法及改进算法的影响；进一步通过仿真分析信噪比、目标角度以及加权系数对两种加权方式性能的影响，明确两种加权方式的适用性；最后将本文提出的加权方法与已有算法进行对比分析。

4.1 两种形式的谱峰搜索公式性能对比

设天线高度100 m，目标距离100 km，地面反射系数为0.9ejπ，阵元数量为8，快拍数为64，直达波入射角 θs=2°，多径角度 θs≈−2.11°，信噪比取-20～20 dB，间隔 5 dB。使用式(7)的角度对应关系，应用3种算法两种形式的谱峰搜索公式在每个信噪比情况下分别进行1000次独立重复试验，统计估计成功概率和均方根误差，结果如图1所示。

图1中，虚线表示式(9)形式的谱峰搜索方式，实线表示式(10)形式的谱峰搜索方式。由图 1可以看出，随着信噪比的增加，各种谱峰搜索方式的成功概率逐渐增加，估计均方根误差逐渐减小。由图1(a)可以看出，相比式(10)形式的谱峰搜索方式，式(9)形式的谱峰搜索方式估计成功概率较低，在信噪比小于10 dB时，成功概率接近为0。在低信噪比时，文献[9]算法的成功概率比广义 MUSIC算法和文献[8]方法要高。这说明了权值对广义 MUSIC算法的估计性能有较大影响。由图1(b)可以看出，式(10)形式下 3种算法的估计均方根误差相差不大。值得注意的是，广义 MUSIC算法的估计成功概率曲线和均方根误差曲线与文献[8]方法对应的曲线几乎重合，说明二者的估计性能是相似的。

4.2 加权系数的分析

保持 4.1节的基本参数不变，当直达波入射角分别取 θd= 1°,3°,5°,7°，加权系数m在0.1～5.9之间变化，变化间隔为0.1，信噪比取−10 dB,−5 dB,5 dB时，利用式(17)，式(18)的权值，分别进行1000次独立重复试验，统计估计结果的成功概率和均方根误差，结果如图2，图3所示。

图2中蓝色曲线为式(17)加权方式对应的仿真结果，红色曲线为式(18)加权方式对应的仿真结果。由图 2可以看出，式(17)加权方式的估计成功概率在加权系数小于1时较高，在加权系数大于1时，受目标角度、信噪比的影响较大。式(18)加权方式的估计成功概率在加权系数大于 1.1时较高，几乎不受目标角度的影响；在加权系数小于1时，估计成功概率较低。因此，在分析两种加权方式的估计性能时，对于式(17)的加权方式，可主要关注加权系数小于 1的部分；而对于式(18)的加权方式，则要关注加权系数大于1的部分。

图3中蓝色曲线为式(17)加权方式对应的仿真结果，红色曲线为式(18)加权方式对应的仿真结果。由图3(a)，图3(b)，图3(c)可以看出，对于式(17)的加权方式，估计均方根误差随加权系数的增加总体呈下降趋势(m<1)；随着目标角度、信噪比的增加，适当减小加权系数可提升估计性能；由图3(d)可以看出，当目标角度进一步增加时，估计均方根误差曲线呈现递减趋势。而对于式(18)的加权方式，随着加权系数的增加，估计均方根误差曲线存在一个驻点，位于m=1.1处。当目标角度由3°变到5°时，驻点位置大于1.1。当信噪比进一步增高、目标角度增大时，估计均方根误差曲线随着加权系数的增加而下降。因此在目标角度较大的情况下，应用式(18)的加权方式时可适当增加加权系数，估计性能会有所提升。综合考虑估计成功概率和均方根误差两个指标，在没有目标角度先验信息的情况下，取式(18)加权方式 m=1.1是比较合理的选择。

图2 不同加权系数时的估计成功概率对比Fig.2 Probability comparison of successful estimation of different weighted coefficient

4.3 不同方法的性能对比

保持 4.1节的基本参数不变，当目标角度分别取θd= 1°,3°,5°,7°时，信噪比取−10～20 dB，间隔5 dB，对比文献[8]，文献[9]和利用式(18)加权方式m=1.1时3种算法的估计成功概率及均方根误差，结果如图4所示。

由图4可以看出，随着信噪比的增加，3种算法的估计性能逐渐变好。与已有方法相比，本文算法具有更高的估计成功概率。当目标角度值为1°时，3种算法的估计均方根误差接近，但本文算法的成功概率更高，在信噪比为−10 dB时，本文算法仍能保证0.8的成功概率；当目标角度为3°时，本文算法在估计成功概率和均方根误差两方面都有优势；目标角度为5°和7°时，本文算法在加权系数m=1.1时，估计均方根误差并没有明显优于已有算法。由4.2节的分析结果可知，当目标角度较大时，可适当增大加权系数。图4(g)，图4(h)给出了 m=1.1,2.5,4.5,5.5时的估计成功概率和均方根误差曲线，可以看出，当目标角度为 7°时，估计成功概率都为 1。而随着加权系数的增大，本文算法的估计均方根误差减小，明显优于已有算法。

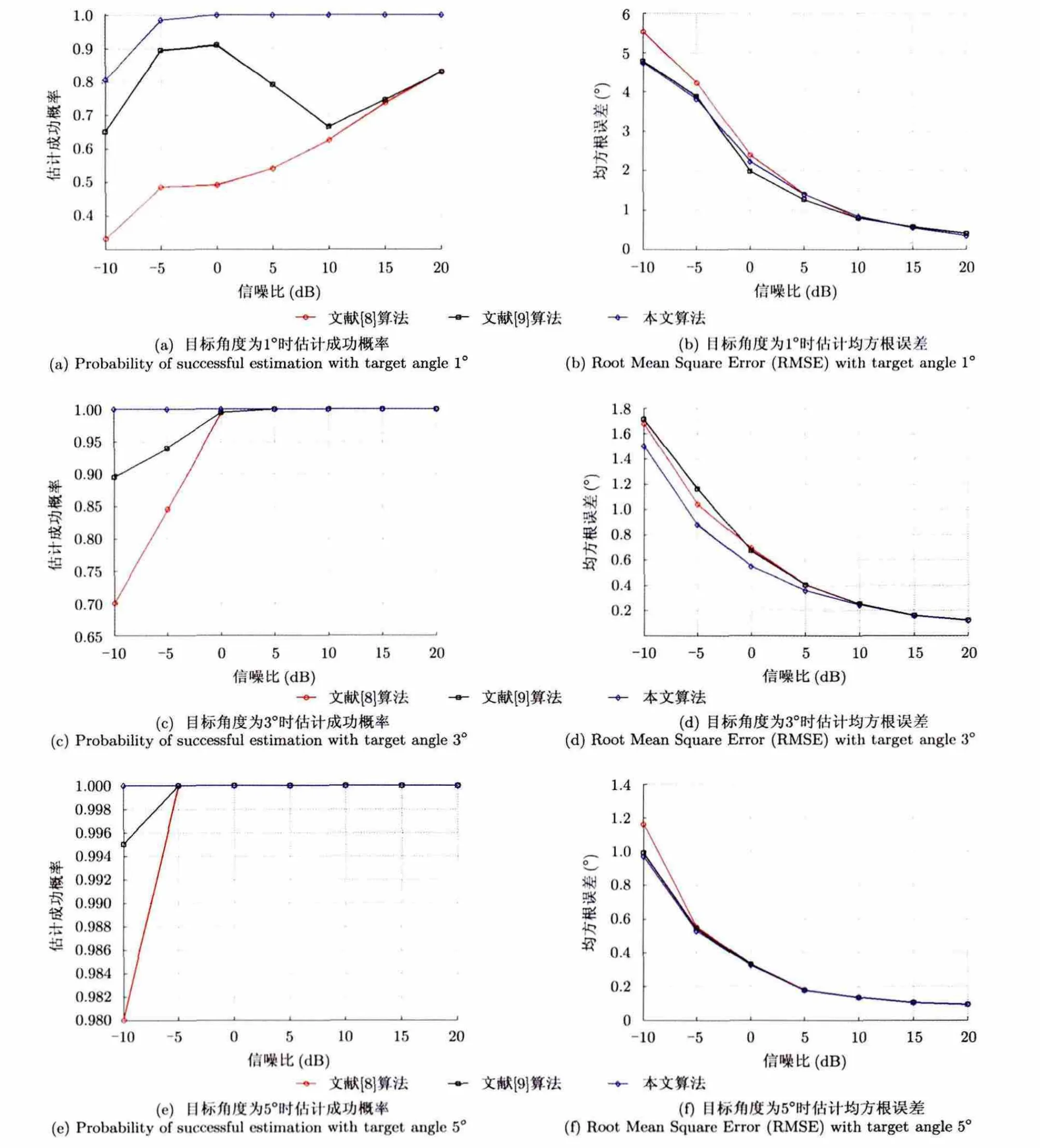
图4 不同算法的估计性能对比Fig.4 Estimation comparison of different algorithms

5 结束语

针对多径环境下的目标低仰角估计问题，本文首先介绍了广义 MUSIC算法及两种改进算法，理论分析指出，这些算法有效性的实质是对基本谱峰搜索公式的加权，3种算法可以统一在加权模型下。不同算法之间角度估计性能的差异正是由权值的差异造成的。在此基础上，本文提出了两种权值可调的加权方式，并通过仿真试验确定了一个性能较优的权值。本文进一步通过仿真对比分析了已有3种算法与基于该权值算法的角度估计性能，仿真结论指出，基于该权值的算法具有更高的估计成功概率，在多数情况下，估计均方根误差优于已有算法或与已有算法一致。利用目标角度的先验信息，通过调整权值，可获得更优良的角度估计性能。权值是影响角度估计性能的重要因素，本文提出的加权方式模型较为简单，因此下一步的工作重点将放在权值设计准则的探讨与权值的优化设计上。

[1]董枚,张守宏,吴向东.距离高分辨测高技术[J].火控雷达技术,2006,34(1): 10-14.Dong Mei,Zhang Shou-hong,and Wu Xiang-dong.A technique of applying high-range-resolution to height finding[J].Fire Control Radar Technology,2006,34(1): 10-14.

[2]陈伯孝,胡铁军,郑自良,等.基于波瓣分裂的米波雷达低仰角测高方法及其应用[J].电子学报,2007,35(6): 1021-1025.Chen Bo-xiao,Hu Tie-jun,Zheng Zi-liang,et al..Method of altitude measurement based on beam split in VHF radar and its application[J].Acta Electronic Sinica,2007,35(6):1021-1025.

[3]Chen Bai-xiao,Zhao Guang-hui,and Zhang Shou-hong.Altitude measurement based on beam split and frequency diversity in VHF radar[J].IEEE Transactions on Aerospace and Electronic Systems,2010,46(1): 3-13.

[4]Shan T J,Wax M,and Kailath T.On spatial smoothing of estimation of coherent signals[J].IEEE Transactions on Acoustics,Speech,and Signal Processing,1985,33(4):806-811.

[5]贾永康,保铮.利用多普勒信息的波达方向最大似然估计方法[J].电子学报,1997,25(6): 71-76.Jia Yong-kang and Bao Zheng.Maximum likelihood DOA estimation by using doppler information[J].Acta Electronica Sinica,1997,25(6): 71-76.

[6]赵光辉,陈伯孝,董枚.基于交替投影的 DOA估计方法及其在米波雷达中的应用[J].电子与信息学报,2008,30(1):224-227.Zhao Guang-hui,Chen Bo-xiao,and Dong Mei.A new DOA estimator based on alternating projection and its application in VHF radar[J].Journal of Electronics & Information Technology,2008,30(1): 224-227.

[7]Zoltowski M and Haber F.A vector space approach to direction finding in a coherent multipath environment[J].IEEE Transactions on Antennas and Propagation,1986,34(9): 1069-1079.

[8]张文俊,赵永波,张守宏.广义 MUSIC算法在米波雷达测高中的应用及其改进[J].电子与信息学报,2007,29(2): 387-390.Zhang Wen-jun,Zhao Yong-bo,and Zhang Shou-hong.Altitude measurement of meter-wave radar using the general MUSIC algorithm and its improvement[J].Journal of Electronics & Information Technology,2007,29(2): 387-390.

[9]刘俊,刘铮,刘韵佛.米波雷达仰角和多径衰减系数联合估计算法[J].电子与信息学报,2011,33(1): 33-37.Liu Jun,Liu Zheng,and Liu Yun-fo.Elevation angle and multipath fading coefficient joint estimation algorithm in VHF radar[J].Journal of Electronics & Information Technology,2011,33(1): 33-37.

[10]Zhang Yu-feng,Ye Zhong-fu,and Liu Chao.Estimation of fading coefficients in the present of multipath propagation[J].IEEE Transactions on Antennas and Propagation,2009,57(7): 2220-2224.

[11]刘俊,刘峥,谢荣,等.互耦条件下米波雷达角度估计的自校正算法[J].电波科学学报,2011,26(6): 1046-1051.Liu Jun,Liu Zheng,Xie Rong,et al..Auto-calibration angle estimation algorithm for VHF radar in the presence of mutual coupling[J].Chinese Journal of Radio Science,2011,26(6):1046-1051.

[12]胡晓琴,陈建文,王永良.米波雷达测高多径模型研究[J].电波科学学报,2008,23(4): 651-657.Hu Xiao-qin,Chen Jian-wen,and Wang Yong-liang.Research on meter-wave radar height-finding multipath model[J].Chinese Journal of Radio Science,2008,23(4): 651-657.

[13]王永良,陈辉,彭应宁,等.空间谱估计理论与算法[M].北京:清华大学出版社,2004: 19-30,83-88.Wang Yong-liang,Chen Hui,Peng Ying-ning,et al..Spatial Spectrum Estimation Theory and Algorithms[M].Beijing:Tsinghua University Press,2004: 19-30,83-88.