非线性多智能体网络的分布式包容控制

于 镝，白丽娟，李 铖

（东北石油大学电气信息工程学院，黑龙江 大庆 163318）

其中xi=［xix，xiy］T和vi=［vix，viy］T分别为二维空间中智能体的位置向量和速度向量，并且可以得出ρ1=ρ2=2。在控制协议（5）的作用下，当控制增益参数α＞9，β＞6时，位置跟踪误差曲线和速度跟踪误差曲线如图3和图4所示，智能体运动轨迹如图7所示，可见跟随者渐近收敛到领航者所围成的凸包中且达到相应的期望位置，与推论1的结论相符。

非线性多智能体网络的分布式包容控制

于 镝，白丽娟，李 铖

（东北石油大学电气信息工程学院，黑龙江 大庆 163318）

针对具有本质非线性动态的多智能体网络，研究分布式包容控制问题。假设只有部分个体已知领航者信息，依据相对位置和速度信息设计分布式控制律。基于代数图论、矩阵理论和Lyapunov稳定性分析方法，得出非线性网络实现渐近包容控制的充分条件。当跟随者之间有向强连通且每个跟随者都至少存在一个领航者与其通信，可选取合适的控制增益使得跟随者渐近收敛到由多个领航者所围成的静态凸包中。仿真实例验证了理论分析的正确性和有效性。

非线性动态；多智能体网络；分布式包容控制

0 引言

分布式多智能体协调控制在系统和控制领域是一个非常活跃的研究课题，主要涉及一致性、编队控制、优化、分布式任务分配、估计和协调跟踪等方面的内容［1-3］，在民用和军事上应用广泛。

由于系统本质上是非线性的，所以对非线性系统的研究更具实际意义且备受青睐。同时复杂网络的牵制控制［4-5］和稳定性分析［6］为非线性多智能体网络一致性的研究提供了理论依据。在假定本质非线性动态满足Lipschitz条件的前提下，文献［7］将线性网络的代数连通度的概念推广到非线性网络中，研究非线性二阶无向网络的一致性问题；文献［8］基于智能体之间的相对状态设计分布式控制协议，并通过求解一组矩阵不等式来实现无向连通网络的全局一致性；针对有向网络拓扑，文献［9］则采用牵制控制实现二阶非线性网络的领航—跟随一致。以上研究均限于无领航和单领航的情况。

而本文所研究的包容控制问题，存在多个领航者且限制跟随者运动到由领航者所围成的最小几何空间内，具有大量的潜在应用。例如，一组智能体把民用物资移动到安全地段，此时只有部分智能体配有传感器来探测危险目标，一般称这些智能体为领航者，称其它智能体为跟随者。通过探测危险障碍物的位置，领航者形成一个安全的区域。若跟随者能搬运物资移动并停留在由领导者所构成的安全区域内，则该组智能体安全地完成任务。文献［10］针对固定无向网络提出停—走策略，从而驱使一组单积分个体进入到由领航者所构成的凸多面体中。文献［11］针对单积分网络，分别研究无向切换拓扑和有向固定拓扑情况下的包容控制问题，并且针对双积分网络，基于相对位置和速度矢量设计分布式控制协议，从而实现有向切换拓扑情况下的渐近包容控制［12］。以上均针对线性网络，而在跟随者和领航者具有相同动态的情况下，文献［13］通过选取合适的控制增益实现一阶有向非线性网络的渐近包容控制，为非线性网络的包容控制提供了新思路。

本文在文献［13］的基础上，进一步研究二阶非线性多智能体网络在有向拓扑结构下的包容控制问题。假设跟随者之间有向强连通且只有部分个体得知静态领航者位置信息，基于相对局部信息设计分布式控制律。从而选取合适的控制增益驱使跟随者渐近收敛并停留在由多个领航者所围成的凸包中。本文的贡献有：与文献［7-9］相比，研究了多领航-跟随一致性问题，与无领航和单领航一致性相比更加复杂；与文献［10-13］相比，研究了二阶非线性多智能体网络的包容控制，更加具有实际意义。

1 相关理论知识

定义1 令Q是实向量空间V⊆Rn的集合，如果对于任何z∈［0，1）和集合Q中任何x，y，都有点（1-z）x+zy在集合Q中，则称Q是凸的。对于V中点X=｛x1，…，xn｝的凸包是指包含X中所有点的最小凸集，用Co｛X｝表示，则

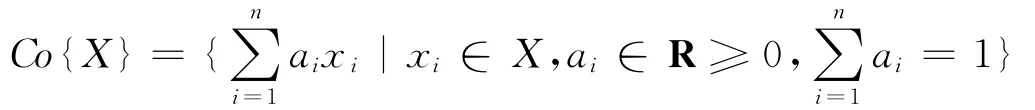
定义2 实数阵A=［aij］∈Rn×n若同时满足：1）当i≠j时，aij≤0；2）对于任意向量x≠0，都存在正对角矩阵D，满足xTADx＞0。则称矩阵A为M 矩阵。若A-1存在，则矩阵A为非奇异M 阵。

2 问题描述

考虑由n个智能体构成的有向网络，其中包括m个跟随者和n-m个领航者。分别用Vf=｛1，…，m｝和Vl=｛m+1，…，n｝表示跟随者集合和领航者集合。本文的控制目的是使跟随者渐近收敛到由多个静态领航者所围成的凸包中。

2.1 网络动态

跟随者的动力学模型为

其中，xi∈Rp和vi∈Rp分别为跟随者的位置和速度矢量，f（t，xi，vi）为非线性动态，i∈Vf。令xf=［x，…，x］T，vf= ［v，…，v］T，F（t，xf，vf）= ［f（t，x1，v1）T，…，f（t，xm，vm）T］T。

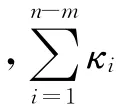
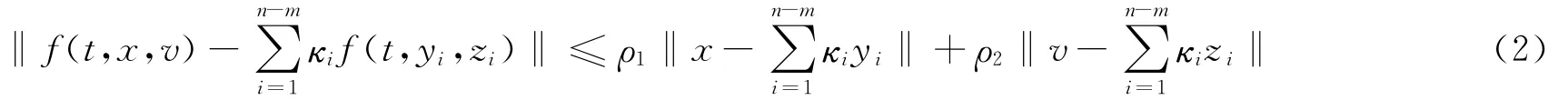
其中，x，yi，v，zi∈ Rp，t≥0，ρ1，ρ2为已知正常数，‖·‖ 表示 Euclidean范数。当存在一个领导者，即n=m+1时，假设条件1为Lipschitz条件，大部分非线性系统均满足该条件。

领航者的动力学模型为

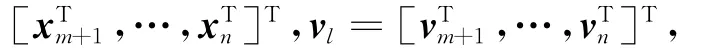
2.2 网络拓扑

令领航者之间无通信，且领航者与跟随者之间的通信是单向的，即领航者发送信息，跟随者接收信息。跟随者之间强连通，且每个跟随者都至少存在一个领航者与其通信。则有向网络的Laplacian矩阵L可以写成分块矩阵的形式：

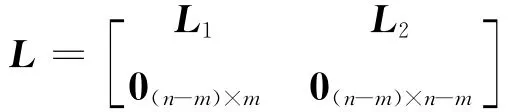
其中，L1∈ Rm×m，L2∈ Rm×（n-m）。

引理1 L1为非奇异矩阵且正定，且-LL2是行和为1的正定阵［12］。

2.3 网络跟踪误差

3 主要结果

设计分布式控制律

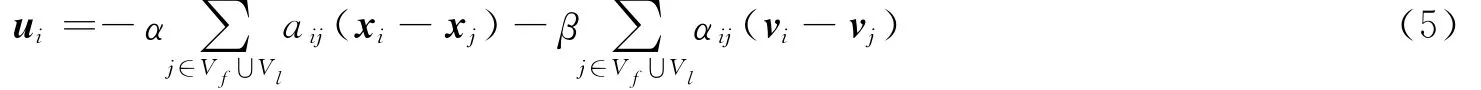
定理1 针对由动态为（1）的跟随者和动态为（3）的领航者所构成的多智能体网络，若假设1成立，跟随者之间强连通，且每个跟随者至少存在一个领航者与其通信。在控制协议（5）的作用下，如果控制增益参数α，β满足

若控制增益满足α＞（ρ1+1）χ，β＞ρ2χ，则＜0。即当t→∞时，跟踪误差ex→0，ev→0。此时跟随者渐近收敛到领航者所围成的凸包中，且达到相应的期望位置。

可见，控制增益α，β的下界与网络拓扑及ρ1，ρ2有关，在系统的网络拓扑信息明确且ρ1，ρ2已知的情况下，该控制方法成立且有效。

推论1 针对由动态为（1）的跟随者和动态为（3）的领航者所构成的多智能体无向网络，若假设1成立，跟随者之间无向连通，且每个跟随者至少存在一个领航者与其通信。在控制协议（5）的作用下，如果控制增益参数α，β满足

4 仿真实例

通过对两种网络拓扑结构的实例仿真来验证理论分析的正确性和有效性。

实例1 网络拓扑如图1所示，其中li，i=1，2，3，4代表领航者，fi，i=1，…，6代表跟随者。可见跟随者之间无向连通，且至少有一个领航者和每个跟随者通信。在二维空间考虑包容控制，非线性动态为实例2 网络拓扑如图2所示，其中li，i=1，2，3，4代表领航者，fi，i=1，2，3，4代表跟随者，可见跟随者之间有向强连通。智能体的本质非线性动态与实例1中的相同。在控制协议（5）的作用下，当控制增益参数α＞17，β＞11时，位置跟踪误差曲线和速度跟踪误差曲线如图5和图6所示，智能体运动轨迹如图8所示。可见跟随者渐近收敛到领航者所围成的凸包中且达到相应的期望位置，与定理1的结论相符。

其中xi=［xix，xiy］T和vi=［vix，viy］T分别为二维空间中智能体的位置向量和速度向量，并且可以得出ρ1=ρ2=2。在控制协议（5）的作用下，当控制增益参数α＞9，β＞6时，位置跟踪误差曲线和速度跟踪误差曲线如图3和图4所示，智能体运动轨迹如图7所示，可见跟随者渐近收敛到领航者所围成的凸包中且达到相应的期望位置，与推论1的结论相符。

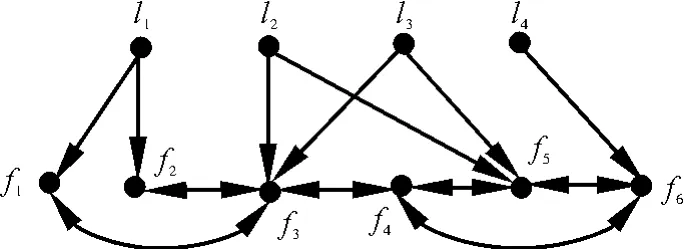
图1 网络拓扑图1Fig.1 Network topology No.1

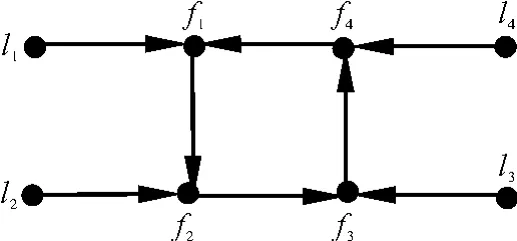
图2 网络拓扑图2Fig.2 Network topology No.2

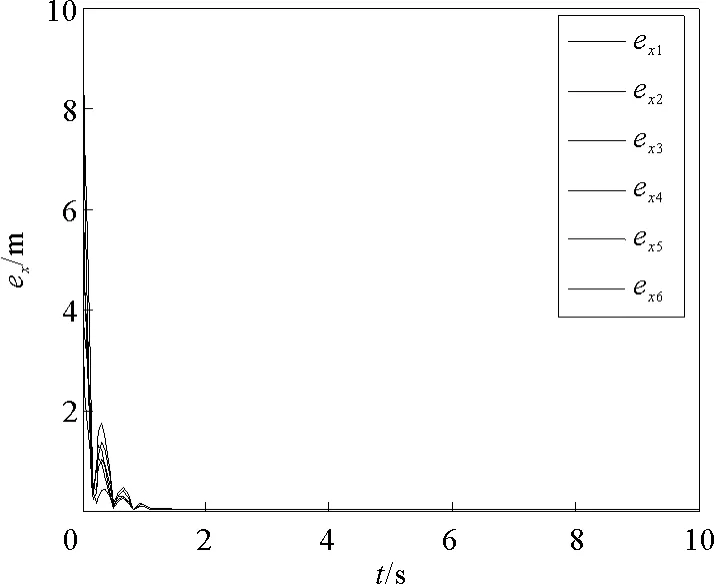
图3 跟随者的位置跟踪误差曲线（拓扑图1）Fig.3 The position tracking error curves of followers under the network topology of Fig.1

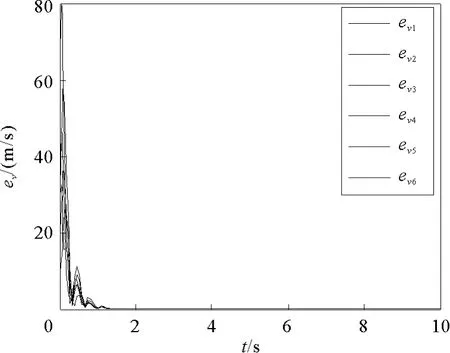
图4 跟随者的速度跟踪误差曲线（拓扑图1）Fig.4 The velocity tracking error curves of followers under the network topology of Fig.1

图5 跟随者的位置跟踪误差曲线（拓扑图2）Fig.5 The position tracking error curves of followers under the network topology of Fig.2

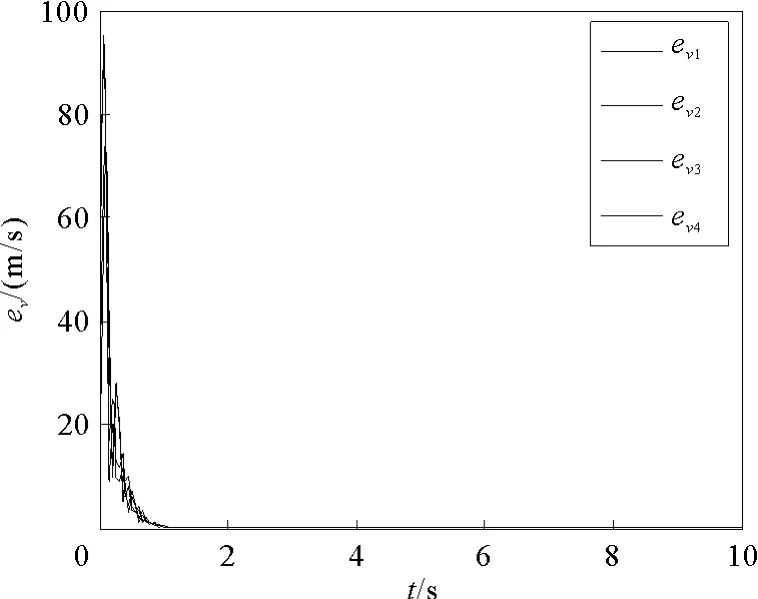
图6 跟随者的速度跟踪误差曲线（拓扑图2）Fig.6 The velocity tracking error curves of followers under the network topology of Fig.2

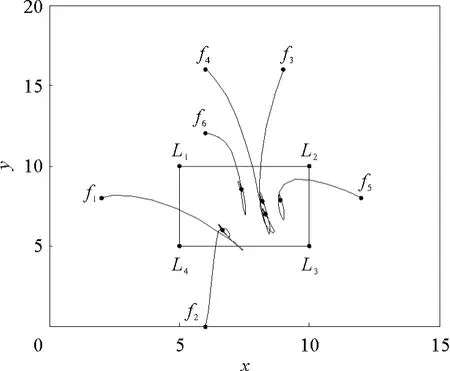
图7 智能体运动轨迹（拓扑图1）Fig.7 The trajectories of agents under the network topology of Fig.1

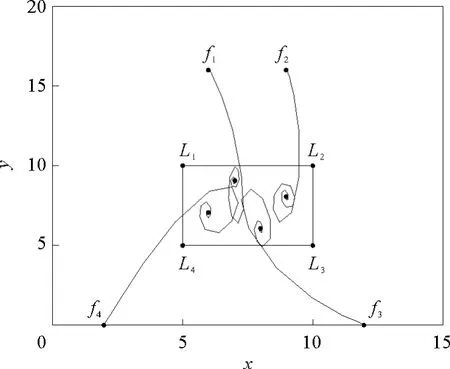
图8 智能体运动轨迹（拓扑图2）Fig.8The trajectories of agents under the network topology of Fig.2

5 结论

本文讨论了非线性多智能体网络的包容控制问题。假设跟随者有向强连通且每个跟随者至少存在一个领航者与其通信，基于相对位置和速度矢量信息设计分布式控制协议。并从网络跟踪误差入手，应用矩阵理论和Lyapunov稳定性分析方法，得出通过选取合适的控制增益可致使跟随者渐近收敛并停留在由领航者围成的凸包中。最后通过仿真实例验证了所提方案的正确性和有效性。下一步将考虑智能体网络势能的变化，针对包容控制中的避碰问题进行深入研究。

［1］Daneshfar F，Bevrani H.Multi-agent systems in control engineering：a survey［J］.Journal of Control Science and Engineering，2009，28（1）：1-12.

［2］Olfati-Saber R，Fax A J，Murray R M.Consensus and cooperation in networked multi-agent systems［J］.Proceedings of the IEEE，2007，95（1）：215-233.

［3］Ren W，Cao Y C.Distributed Coordination of Multi-Agent Networks［M］.London：Springer，2010：3-34，99-142.

［4］Yu W W，Cao G R，L J H.On pinning synchronization of complex dynamical networks［J］.Automatica，2009，45（2）：429-435.

［5］Li X，Wang X F，Chen G R.Pinning a complex dynamical network to its equilibrium［J］.IEEE Transactions on Circuits and Systems-I：Regular Papers，2004，51（10）：2074-2087.

［6］Chen G R.Stability of nonlinear system［M］//Chang K.Encyclopedia of RF and Microwave Engineering.New York：Wiley，2004：4881-4896.

［7］Yu W W，Chen G R，Cao M，et al.Second-order consensus for multi-agent systems with directed topologies and nonlinear dynamics［J］.IEEE Transactions on Systems，Man，and Cybernetics-Part B：Cybernetics，2010，40（3）：881-891.

［8］Li Z K，Liu X D，Fu M Y.Global consensus control of lipschitz nonlinear multi-agent systems［C］//Preprints of the 18th IFAC World Congress.Milano，Italy，2011：10056-10061.

［9］Song Q，Cao J D，Yu W W.Second-order leader-following consensus of nonlinear multi-agent systems via pinning control［J］.Systems &Control Letters，2010，59（9）：553-562.

［10］Mei J，Ferrari-Trecate G，Egerstedt M，et al.Containment control in mobile networks［J］.IEEE Transactions on Automatic Control，2008，53（8）：1972 1975.

［11］Cao Y C，Ren W.Containment control with multiple stationary or dynamic leaders under a directed interaction graph［C］//Joint 48th IEEE Conference on Decision and Control and 28th Chinese Control Conference.Shanghai，China，2009：3014-3019.

［12］Mei J，Ren W，Ma G F.Distributed containment control for multiple nonlinear systems with identical dynamics［C］.Proceedings of the 30th Chinese Control Conference.Yantai，China，2011：6544-6549.

［13］Cao Y C，Stuart D，Ren W，et al.Distributed containment control for double-integrator dynamics：algorithms and experiments［C］//2010American Control Conference，Marriott Waterfront，Baltimore，MD，USA，2010：3830-3835.

Distributed Containment Control of Nonlinear Multi-Agent Networks

YU Di，BAI Li-juan，LI Cheng
（Northeast Petroleum University，School of Electrical Engineering and Information，Daqing 163318，China）

Distributed coordinated containment control problem is studied for multi-agent networks with inherent nonlinear dynamics.Distributed control law is designed according to relative positions and velocities assuming that only a subset of agents know information of leaders.Sufficient conditions are developed to achieve asymptotic containment control based on algebraic graph theory，matrix theory and Lyapunov stability analysis method.Followers can be driven into stationary convex hull asymptotically，which is formed by leaders with suitable control gain when followers are strongly connected and every follower communicate with a leader at least.At last two simulation examples are given to prove the correctness and validity of the theoretical analysis.

nonlinear dynamics；multi-agent network；distributed containment control

TP273

A

1672-3813（2013）02-0063-06

2012-12-04

于镝（1977-），女，黑龙江安达人，博士，副教授，主要研究方向为多智能体协调控制和非线性控制。

（责任编辑 李进）