在线社交网络的逻辑模型和并行查询
李伟钢,郑建亚
(巴西利亚大学计算机系TransLab实验室,巴西利亚70910- 900)
在线社交网络的逻辑模型和并行查询
李伟钢,郑建亚
(巴西利亚大学计算机系TransLab实验室,巴西利亚70910- 900)

归纳出对在线社交网络研究具有挑战性的一些课题,介绍描述用户关系的逻辑模型(粉丝模型),提出逻辑关系寓意邻接矩阵(粉丝矩阵)。用此模型展示对微博平台Top-X信息查询的聚合-排序-删除算法。进一步应用映射和化简概念将上述Top-X信息查询算法扩展于并行计算环境,给出映射关注和化简粉丝在Hadoop系统联机实现的算法。粉丝模型和相应的算法实现了对新浪微博74.7GB和Twitter的101GB实际数据的多种约束下信息查询和微博转发预测,特别是在Hadoop系统联机环境下,新方法的信息化简和计算性能明显提高。
复杂网络;平行算法;微博;信息查询;映射和化简;在线社交网络
0 引言
在线社交网络具有动态变化、在线即时、个性行为、异构互联和大数据生成等特点。基于浩瀚网络拓扑、海量数据处理、多重关系分析和信息传播扩散等对其机制进行研究,面临着理论建模和技术实践的各项挑战。国内外若干著名智能网络、数据挖掘和复杂系统等研究中心,无不投入大量人力物力,从事这方面研究。
梳理新近文献,发现对社交网络信息传播机制的研究离不开对图论的完善以及数据挖掘的深入研究,同时还具有以下特点:Jiawei Han团队等提出异构信息网络理论,对大型信息技术文献库DBLP的论文引用和共同作者进行预测[1]。亚洲微软Haixun Wang团队提出10亿节点巨型网络子图匹配的分布式优化算法,大大提高了网络咨询分析效率[2]。加州大学圣塔芭芭拉分校的Ben Y Zhao团队注重在线网络大尺度和多层次的动态特性,研究微博海量信息分布和传播机制[3]。卡内基梅隆大学的C Faloutsos团队在分析大规模网络,使用云计算进行知识挖掘,完善图论方法等方面的工作值得注目[4]。斯坦福大学J Leskovec团队提出多元素、多关系的新型图论模型,广泛应用于多种网络研究[5]。
国内不少学者和机构也在相关方面进行了卓有成效的研究。例如中国原子能科学研究院方锦清团队近年来致力于推动社交网络研究,对博客-微博网及其特点进行了全面阐述,并对在线社交网络若干研究问题进行了展望[6];清华大学唐杰团队开发应用大型文献库并付诸于实[7];华东师大周傲英团队和四川大学唐常杰团队在大数据和知识发现等方面的工作[8-9];中科院程学旗团队使用传播动力学的方法来进行社区发现[10]并通过分布式计算来提高计算效率,等等。另外,一些物理学和数学方面的专家从复杂网络系统角度,研究社交网络相关模型,如中科大的汪秉宏团队对复杂网络博弈的研究[11]和电子科技大学周涛团队对链路预测等的研究[12],程代展团队通过矩阵半张量积这一创新计算方法对一般逻辑网络进行研究[13],并利用演化博弈来对复杂网络进行建模和分析,等等。2012年参加WISE新浪微博竞赛的若干团队[14-15],也在信息查询和转发预测等方面,进行较全面的研究。
总的来看,当前对在线社交网络的研究已取得了阶段性成果,但实际上,在对在线社交网络和其它复杂信息网络机制研究时,人们往往采取拿来主义,即基于现有图论衍生的网络技术,注重计算技巧,缺乏理论研究。例如,新浪和腾讯等微博是网友在线社交平台,用户间的关系盘根交错,极其复杂[16]。学术界对微博的研究方兴未艾,迅速发展。上面提到的一些科技文献,尽管成效显著,但在网络节点间关系和反映这些关系相互作用方面,来自数学、物理、生物和工程等领域的研究成果,尚无深刻描述和有效模型。尤其是对多层次用户关系的微博转发预测时,经典的邻接矩阵定义和在此基础上研发的数学模型,显得单调,亟需跨学科理论和技术的交叉性研究。本文针对该问题,从以下两方面进行建模研究:一是微博机制的用户关系逻辑描述;二是微博信息查询的高效平行算法。
以新浪微博平台上信息查询和知识挖掘为例[14-15],数亿条微博短信,几千万级的复杂的客户关系数据,简单的查询都需要从海量数据中理清客户关系。本文以多项约束条件下组合为切入点,得出合乎查询要求的Top-X,如常说的前10名、前50或100名。初步研究可以分以下五类较复杂的组合:1)基于微博用户的基本人际关系的组合查询,如粉丝、关注人和互粉关系,可能涉及与一个或多个用户;2)基于用户间发生活动的组合查询,例如发博、提及、评论或转发等活动等,可能涉及与一个或多个活动;3)基于微博、提及、评论或转发等文本的议题和相关社会事件等的组合查询,可能涉及与一项或多项议题或事件;4)基于上述微博关系、活动或事件等的某时间段的组合查询,此时间范围可以是1小时、1天、1周或1年等等。对于这4项内容的任意或特殊的复杂组合查询,考虑到微博用户的关系复杂性、活动多项性、议题丰富性和事件突发性,以及时间间隔和海量数据等特征,可知微博用户信息复杂组合查询的表述和实现是非常艰巨的计算分析活动。
在上述文献研读基础上,本文介绍描述用户关系的逻辑模型,粉丝模型[12],提出逻辑关系寓意邻接矩阵(Relationship Committed Adjacency Matrix-RCAM,简称粉丝矩阵)。用此模型可以展示对微博平台Top-X信息查询的聚合-排序-删除算法。并进一步应用映射和化简[17]概念将上述Top-X信息查询算法适用于并行计算环境,介绍映射关注,化简粉丝算法和在Hadoop系统的联机实现。在对新浪微博74.7GB和Twitter的101GB实际数据的查询和微博转发预测,Hadoop系统联机环境下的新方法在信息存储量化简和计算能力等方面的性能明显提高。
1 用户关系逻辑模型
微博平台上,最常见的社交关系是用户间的关注关系。有一群人被称为“博主”,也有一群人叫做“粉丝”。在这个社区内,如果用户A关注B,称A是B的粉,称B是A的关注人。如果A是B的粉,B亦是A的粉,称A和B为互粉关系。
在线社交网络一般可以描述为有向图:G=(V,E),这里图的节点V表示用户;节点间的有向连接为E:V×V,表示用户间的关系。(A,B)∈E,表明用户A关注用户B,即,A是B的粉,B是A的关注人。
较正式的用户关系数学描述[14]为:对于用户间关系函数fin,fout,fr,V→V*,有:
fout(A)={B|(A,B)∈E},表示A 的关注人集函数,A关注B;
fin(B)={A|(A,B)∈E},表示B的粉丝集函数,A 为B 的粉;
fr(A)=fout(A)∩fin(A),表示A的互粉集函数,A的关注人集合与关注A的粉丝集合之交集。
这些函数把微博用户关系简洁准确地描述出来,为便于分析和应用,暂将其称为粉丝模型。该模型同时具备反对称与对称性、可扩展性和可组合性,使得传统的图论理论在微博机制分析上拓宽了新的逻辑关系表达模式。
1.1 反对称与对称性
从函数的对称意义来看,可以定义其反函数。若f∈{fin,fout,fr},有其反函数f′定义为

定理1 fin和fout互为反函数。
证明:对有向图:G=(V,E),节点V表示用户;节点间的有向连接为E:V×V,表示用户间的关系。(A,B)∈E,表明用户A关注用户B,A是B的粉丝,B是A的关注人。有:
fout(A)={B|(A,B)∈E},表示A 的关注人集函数,A关注B;
fin(A)={B|(B,A)∈E},表示A 的粉丝集函数,B为A 的粉丝;
有反函数:(fout(A))′=({B|(A,B)∈E})′={B|(B,A)∈E}=fin(A);
有反函数:(fin(A))′=({B|(B,A)∈E})′={B|(A,B)∈E}=fout(A);
证得fin和fout互为反函数。
定理2 fr和fr自为反函数。
证明:对有向图:G=(V,E),节点V 表示用户;节点间的有向连接为E:V×V,表示用户间的关系。(A,B)∈E,表明用户A关注用户B,A是B的粉丝,B是A的关注人。如果A是B的粉丝,B亦是A的粉丝,称A和B为互粉关系,有:
fr(A)=fout(A)∩fin(A),表示A的互粉集函数,A的关注人集合与关注A的粉丝集合之并集。
其中,fout(A)={B|(A,B)∈E},fin(A)={B|(B,A)∈E},
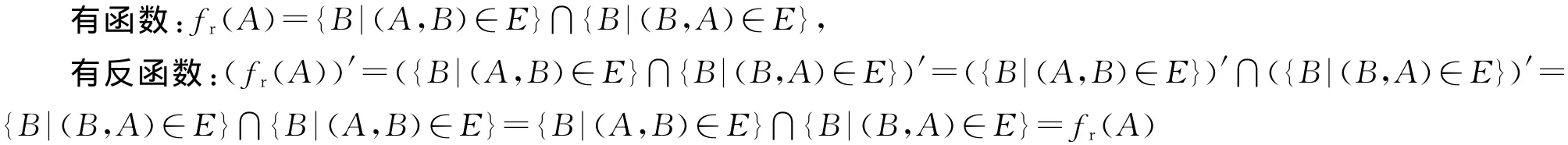
证得fr自为反函数。
1.2 可扩展性
若f1,f2∈{fin,fout,fr},对于用户间关系函数f1,f2,V→V*,则函数间的并集、交集计算为

这里如果f1,f2相同,并集计算有f·f=f2和进一步的f·fn-1=fn。例如,f2in(A)就是A的粉丝的粉丝的集函数;而fnr(A)就是A的互粉的互粉的……互粉的集函数。
对于交集计算,前述的互粉关系函数定义就是特例:fr(A)=fout(A)∩fin(A),这里f1=fout,f2=fin。
1.3 可组合性
考虑到进一步的操作性,这些函数间的组合可表达更多的用户关系,实现相关计算。例如,fin·fout(A)是指A关注人的粉丝集函数,而f2in(A)就是A的粉丝的粉丝集函数。
有了对微博用户关系逻辑描述的粉丝模型的函数定义和特性,具体问题的表达会更方便和实用。若以姚晨博友微博平台的网友关系在线查询为例,这些查询提示可以较正式地用粉丝模型表示。
关注她的人同时关注了……,对应上述定义的微博用户逻辑关系,是对foutfin(A)的求解,A在这里就是博主姚晨,函数集表示关注她的粉丝同时关注的网友。
这些人也关注她……,对应上述定义的微博用户逻辑关系,是对fout(A)∩fin(B)的求解,这里的A是笔者,B是姚晨博主,就是说这个用户集是笔者所关注的网友,同时也是姚晨的粉丝。
我和她都关注了……,对应上述定义的微博用户逻辑关系,是对fout(A)∩fout(B)的求解,这里的A是笔者,B是明星姚晨。函数集表达我和她共同感兴趣的网友。
2 用户关系逻辑模型的邻接矩阵表述
研究各类复杂网络理论时,在高效率计算的意义下,用邻接矩阵来表示网络拓扑,是研究人员的基本选择。随着在线社交网络的蓬勃发展和深入研究,尤其是在关系错综复杂的微博平台内,还没有对用户各种行为和关系给予准确描述的贴切的数学模型,人们越来越感到直接使用邻接矩阵的乏力。
基于粉丝模型[14],注意到在线社交网络用户间的多重、多层的复杂关系和大网络并行计算的潜力,这里进一步提出关系寓意邻接矩阵概念,简称粉丝矩阵。按照粉丝模型的定义,Ain为粉丝邻接矩阵,其转置矩阵就是关注矩阵,具体表示为Aout=ATin。经过多次相乘,Akin=AinAin…Ain是k-阶粉丝矩阵。如果把n个节点的社交网络用n×n矩阵Ain表示,则通过A2in可查询粉丝的粉丝信息;利用AinAout查询关注人的粉丝信息;利用AoutAin查询粉丝的关注人信息等等。
2.1 图和邻接矩阵的定义
为便于描述问题,按图论来定义在线社交网络的元素和关系。4个节点和连接构成一个简单的无向图G=(V,E),如图1所示。节点集V 内有:A,B,C,D∈V;各节点内含一元素,这里指用户名u,v,w 和x;节点间形成无向连接集E:V×V:(A,B),(A,D),(B,C),(B,D)和(C,D)∈E;用户间可能的关系为:(u,v),(u,x),(v,w),(v,x)和(w,x)∈R。
在此定义里,节点和元素、连接和关系是有意分开的,因为网络内的节点和连接一般是不变的,但在线社交网络的元素和关系随时会发生变化。例如,节点可能会是用户,也可能是微博;关系可能是关注关系,也可能是微博转发关系。
邻接矩阵A的定义为A(u,v)=1。如果(u,v)∈E;否则,A(u,v)=0。如果图内有n个节点,则邻接矩阵A的元素为n×n。
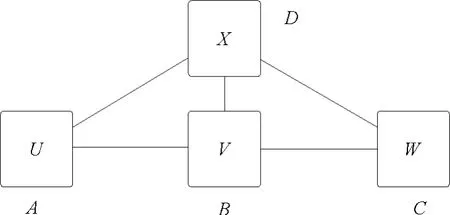
图1 四节点形成的无向图,网络研究的出发点Fig.1 Simple network with four nodes of an undirected subgraph
图论研究表明[18],k-阶邻接矩阵即矩阵的k次连乘,Ak=AA…A。如果两个节点(u,v)间的连接赋予权重为w(u,v),如果(u,v)∈E;否则,w(u,v)=0。w(u,v)可定义为距离、成本或效益。通过计算Ak,可以得出两点间最优k段路经,如果存在这些路径的话。
2.2 粉丝矩阵的定义
结合粉丝模型[14],参照无向无权重图的基本定义,以图1为基础来表征社交网络,加上节点间的指向,表明用户间的关系,参见图2。把上述定义的邻接矩阵赋予这种微博用户间的关系,可使用粉丝矩阵Ain来表达该网络内各用户间的关注关系。如果用户u关注用户v 且 (u,v)∈E,Ain(u,v)=1;否则,Ain(u,v)=0。这里的下标in和粉丝模型的函数fin(.)相对应,表示用户v的粉丝集(即关注v的所有用户集)。如果该图有n个节点,Ain具有n×n元素。
粉丝矩阵Ain描述了相关元素的关注关系,通过对该矩阵行的阅读,查询到有关用户的粉丝信息。粉丝矩阵的转置A,定义为关注矩阵Aout=A。关注矩阵Aout描述了相关元素的关注关系,通过对该矩阵行的阅读,查询到有关用户的关注人信息。
为便于广泛应用,本文通称粉丝矩和关注矩阵为关系寓意邻接矩阵,简称粉丝矩阵。值得提出的是,文献[19]在研究复杂系统结构有序度时,曾定义过反映结构元素间关系属性的关系矩阵。而且,基于负熵的有序度概念,对研究在线社交网络的关系和结构也有现实意义。
在线社交网络用户间的关系并不仅仅是一个层次的关系,而是多层次关系,例如,朋友的朋友的朋友……,就是多层次关系。有了粉丝矩阵,就可以方便地对这些关系加以描述。用A=AinAin…Ain来表达k-阶粉丝关系,A是粉丝矩阵Ain的k次相乘。
2.3 粉丝矩阵的计算实例
使用一简单例子,说明粉丝矩阵Ain,Aout,A的具体计算和实际应用。
图2表达一个简单社交网络,其中各种关系均相对于用户v:用户u关注v和x,用户v关注w和x,用户x关注u和v。在此基础上,列出的粉丝矩阵Ain和关注矩阵Aout的具体表达。
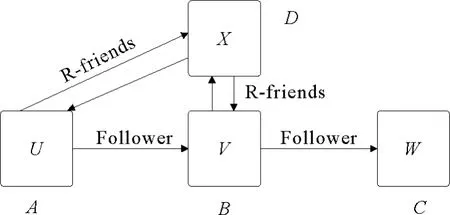
图2 简单在线社交网络中相对于用户v的粉丝、关注和互粉关系Fig.2 Follower,followee and v-friends relationships in online social network

粉丝矩阵Ain第一行,可以表达/查询用户u是v和x的粉丝的信息。关注矩阵Aout第二行,可以表达/查询用户v被u和x关注的信息。
当需要查询朋友的朋友相关信息时,可以运用粉丝矩阵的两阶运算A。从A可看出,用户u的朋友的朋友是v;v的朋友的朋友是u和x;等等。

如果需要查询用户的关注人的粉丝,粉丝矩阵与关注矩阵的乘积,AinAout可提供相应信息。如AinAout所示,用户u的关注人的粉丝为v和x;v的关注人的粉丝为u,等等。
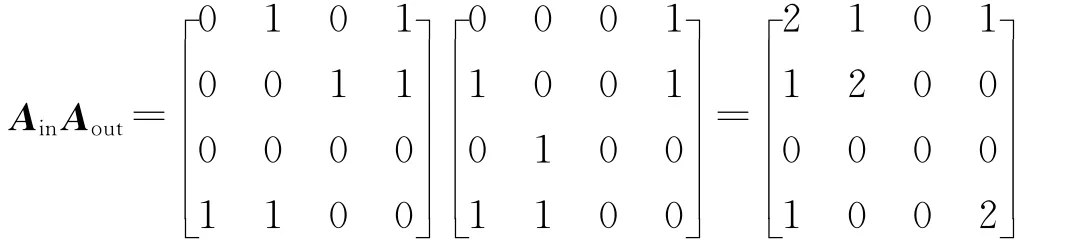
通过粉丝矩阵和关注矩阵的各种组合、各阶计算,可以对在线社交网络的各类相关信息进行查询。这些查询对于微博转发预测和信息传播预测都有着积极的意义。同时,矩阵操作对于开发并行计算资源,意义重大。可以说整个网络各节点的计算都将一次性的甚至是同步的。如果说二阶粉丝矩阵A2in的计算复杂度为O(n3),当k为有限值时,Akin的计算复杂度仍为O(n3)。这一点也是有意义的,在第一次计算A2in后,Akin将会在各项查询和微博转发预测中多次使用,这正是提出关系寓意邻接矩阵的真正意义之一。
3 微博信息查询Top-X的减少数据存储量算法
新颖的社交网络形成海量的大数据,已达到TB甚至PB规模,出于政治、商业和技术等目的的信息查询,如同大海捞针,需要有效的算法来寻找知识性信息。针对引言部分有关微博平台多约束组合信息查询问题,介绍文献[14]提出的基于粉丝模型,在给定时间段内的Top-X的“聚合-排序-删除”查询算法。
3.1 基础查询算法
在线社交网络信息查询的简单通用方法,主要有两种。
3.1.1 有序数据的逻辑乘运算
若想通过微博平台信息查询,得知本人和某人共同关注的用户集。用粉丝模型即:I(a,b)=fout(a)∩fout(b),这里的fout(.)是粉丝模型的某用户关注人的集函数,fout(a)={a1,a2,…,an},fout(b)={b1,b2,…,bn}。这样问题相当于逻辑乘运算,例如,曾博主关注的博主有张、王、李和赵,刘博主关注的博主有张、王、李和黄,则他们共同关注的博主有:张、王和李。
假设需要对集合fout(a)={a1,a2,…,an}和fout(b)={b1,b2,…,bn}求交集。为了使计算更有效率,最好首先对集合内的数据进行排序,如a1<a2<…<an,b1<b2<…<bn。有序数据的逻辑乘运算的时间复杂度为O(m+n),只需要进行简单的合并操作,并标记出在两个集合中都出现的元素。
3.1.2 有序数据的计数运算
如果某用户希望通过自我查询或是微博平台推荐来获得关注对象,最简单的方法是看看他已关注的人的关注人。用粉丝模型就是某用户关注人集函数的两次操作:fout(fout(.))。例如,曾博主关注的博主有张、刘和赵;张博主关注的博主集合内有王、李和黄,刘博主关注的博主集合内有王、陆和姜,赵博主关注的博主集合内有王、李和姜;则系统会根据并集结果向曾博主推荐应该关注的博主有:王、李、姜、黄和陆。其中王博主有3人关注,李和姜博主分别有两人关注,黄和陆博主各有一人关注。
假设有相当于上述张、刘和赵等博主关注的博主集合 m 个:A1={a11,a12,…,a1n1},A2={a21,a22,…,a2n2},……,Am={am1,am2,…,amnm},需要查询在所有集合中重复次数最多的元素。和上述有序数据的逻辑乘运算一样,首先对所有的m个集合进行排序,然后对排序后的集合进行合并,在合并的过程中就可以对每一个元素的出现次数进行统计,最后对元素的出现次数进行排序,得到要查询的结果。在合并的过程中使用堆积树能使算法得到进一步的优化。
上述例子中,得出的结果有5位博主,一目了然。如果得出的推荐集内含成千上万个博主,这就涉及到Top-X问题。此例中,可以把“约束”定义为:关注人多于两人的博主,推荐结果为:王、李和姜。还可以把“约束”定义为前 X 名粉丝最多的博主,相应的粉丝模型函数应为:fin(fout(fout(.)))。
3.2 时间区间内的查询:数据索引法
前面的查询举例仅涉及用户间的基本关系,与时间因素关系不大,如果要查询用户间发或转发微博、推荐、评论和提醒等互动行为,则与时间关系密切。例如,用户希望查询在时间区间[ta,tb]内,粉丝对其微博的转发次数等,就需要重新分析问题,研究新的查询算法。
例如,王博主(A)发的微博,在t1和t2时被某两粉丝转发,张博主(B)的微博在t3时被某粉丝转发。微博被转发一次,称为一项事件,标记为ek,在时间区间[t1,t3]内,共发生3项事件。可以用集合S表示这些事件和发生的时间:S={(eA,t1),(eA,t2),(eB,t3)};用集合C 表示与某用户有关的事件发生时间:如王博主的微博被转发的事件eA的时间集:C(eA)={t1,t2},张博主的微博被转发的事件eB的时间集:C(eB)={t3}。
还有另外一种表示方式。假设集合S={(e1,t1),(e2,t2),…,(en,tn)}表示一系列的事件和其发生时间。使用集合C(ek)={t1,t2,…,tm}表示S中事件ek发生的时间集合,那么m=|C(ek)|就表示事件ek发生的次数。同样使S[ti,tj]表示在[ti,tj]时间范围内事件ek发生的集合。
如果需要查询ek在时间段S[ti,tj]内的出现次数,如果数据集S过大,进行遍历查询的工作量很大,效率非常低。一个优化的方法就是为每一个事件ek维护一个按发生时间排序的列表C(ek)={t1,t2,…,tm},其中t1<t2<…<tm。通过二叉树查找算法,以O(log(n))的复杂度找到第一个tx>ta和第一个ty>tb的事件元素。因此,事件ek的出现次数就是这两事件序号之差。
图3表示事件ek发生13次的时间分布轴,数值1表示ek第一次发生,13表示ek第13次发生。在ta和tb时间区间内事件发生的次数就是出现在tb之后的事件的第一个序号减去ta之后事件的第一个序号,既是9-6=3,说明在时间区间[ta,tb]内,事件ek发生了3次。
以上3种算法都是运用了有序数据可以提高查询效率的基本原理。用数据索引法来查询时间区间[ta,tb]内某事件的发生次数。实际工作中,有两方面的问题:一是查询计算不具备再利用性,特别是在数据集较大情况下,费很大力气查得某事件的次数后,如果需要查询另一事件,还要重新查询。同时,查询时间区间变化后,新的查询也要从头开始。二是,当需要查询时间区间[ta,tb]内出现次数最多的某事件及相关用户的Top-X时,用数据索引法计算该事件的出现次数,然后求出Top-X来,这只是在数据集比较小的时候,方能奏效。对于大数据,需要开发高效并可重复利用的算法。
3.3 聚合-排序-删除算法
考虑到在线社交网络的特性和对信息Top-X查询的困难,文献[14]提出“聚合-排序-删除”算法,通过保留含有效信息的数据,大量减少存储量的方法,来优化计算,实现此类查询。
3.3.1 聚合
首先定义查询时间区间为[ta,tb],根据客户需要可取为1小时、1天、1个月或1年等等。然后,将时间轴划分成连续的、相等间隔的时间片Δt,一般取值为10分钟、半个小时等等。对于每一个时间片S[ts,ts+Δt],计算出每个事件ek相关的两个指标:min(ek,ts)和 max(ek,ts)。其中 min(ek,ts)代表事件ek在给定时间区间[ti,tj]内的最小出现次数,并且,tj∈[ts,ts+Δt]和tj-ti=tb-ta。同理,max(ek,ts)就是在这个时间片内结束的时间区间内,事件ek出现的最大次数。
图4给出聚合过程的一个具体例子,其中事件ek在整个时间轴上发生了13次,每次发生的时间如图4时间轴所示。时间轴下面的数字曲线展示了每个时刻在指定的时间区间内事件的发生次数。假设时间区间隔是1个小时,那么在第8次之前的1个小时内,ek共发生了3次。若将时间轴划分成均等的时间片Δt=20 min,计算时间区间内所含的时间片事件发生次数的最小值和最大值。就图4的例子来说,在该指定的时间区间内,第7、8次的时间片内ek发生次数的最小值为1,最大值为3。

图3 数据索引法步骤Fig.3 Data indexing method procedure
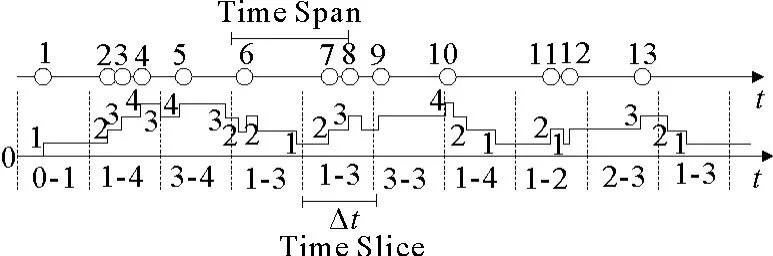
图4 事件聚合步骤Fig.4 Event aggregation procedure
3.3.2 排序
聚合方法存储了所有时间片内事件发生的信息,这种操作会占用大量的存储空间,就聚合本身来讲,是一个费时和费空间的低效方法。为了减少占用空间,需要删除那些对要求的查询结果无关的信息。因为查询的要求最大情况下为Top-X,以X=100为例,只需要保留那些对Top-100有关的信息就可以。这样,对于每一个时间片,通过发生最小值 min(ek,ts)递减排序得到该时间区间发生次数的列表(e1,e2,…,e99,e100,e101,…,en)。必须始终保持前100的值,然而如果一个时间发生的最小值不在前100以内,但是它发生次数的最大值大于min(e100,ts),那么同样也要放在该序列内。通过这个方法,即可大大减少算法对空间的需求,也就是说,减少了千千万万无查询价值的事件发生的最大值和最小值。
删除过程就是减少对查询结果无用信息的储存,大大减少对无关数据的处理。同样,可以将ARD过程循环使用,以便得到更小的Δt时间片内相关信息,提高查询范围。
3.3.3 删除
图5描述了确定时间片内数据的信息保留和删除过程。例如,在每一个时间片上相对纵坐标的事件A,B,C的最大值和最小值的排序位置。如果查询只求Top 1的话,那么列表中只维护两种信息:1)具有最大max值和相应min值的事件,如图5第一时间片中的A事件;2)max值大于保留事件的min值的事件,如图5中第一时间片中的B、C事件。在图5中的其它事件片内,被去除掉的元素已用X标识。
需要指出的是,考虑到多个时间区间查询需求,如1小时、1天、1个月甚至1年等,需要为每一个时间区间维护一个序列,但由于时间片选取的标准化,这样的计算并不费事。例如上例中,时间片为20分钟,时间区间为1小时,则一个时间区间由3个时间片组成。而时间区间为一天时,一个时间区间由72个时间片组成。实际计算时,这些工作并不困难,这主要是聚合-排序-删除算法考虑到Top-X的限制,使得大数据集的计算问题变成小数据集的计算。例如,在查询转发某微博的用户粉丝Top-50时,删除后应存储的数据量仅需8%左右。
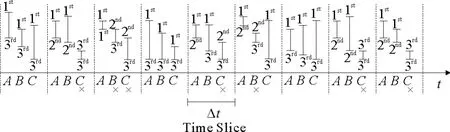
图5 排序和无用信息删除步骤Fig.5 The procedure of ranking and useless information deletion
4 微博信息查询Top-X的平行算法
随着在线社交网络用户的激增,平台上相应的功能也在不断完善,微博信息查询也面临着新挑战。例如国内一些微博平台在原有的转发、提及和评论等动作之外,还增加了推荐功能。在这些平台上发现谁是谁的粉丝,谁的粉丝最多,这都不是太大的问题,如前面章节介绍的粉丝模型和查询算法都相应提及。
比较棘手的问题是在给定时间区间[ta,tb]内,查找转发(或者推荐、提及或推荐等)某些用户在一动态群体内的粉丝数等信息的Top-X。这种动态形成的用户集合,微博平台并没有现成的排行结果,他们也需要即时在线查询。本节提出的Top-X查询平行算法就是针对这一实际问题,应用映射和化简概念[17],在Hadoop系统支持下,联机跨平台上实现。
假设在给定时间区间[ta,tb]内转发一用户微博的用户集为Z=[A,B,C,…,P,Q,R,…],共m 个。正常情况是查询出该集合内各用户的关注人的集合fout(X),X=A,B,C,…,P,Q,R,…。这个查询的空间几乎是微博平台的所有用户,工作十分艰巨。如果把这个查询过程在Hadoop平台实现,就是所谓的映射过程,其间利用平行计算的模式,大大提高了计算效率。其具体算法如表1所示。
映射关注和化简粉丝算法查询微博平台的Top-X:
1)建立关系对过程,建立转发一用户微博的m个用户集为Z=[A,B,C,…,P,Q,R,…]的关注关系对,如表1中,User A关注User P等等,这些关系对一般大于m。
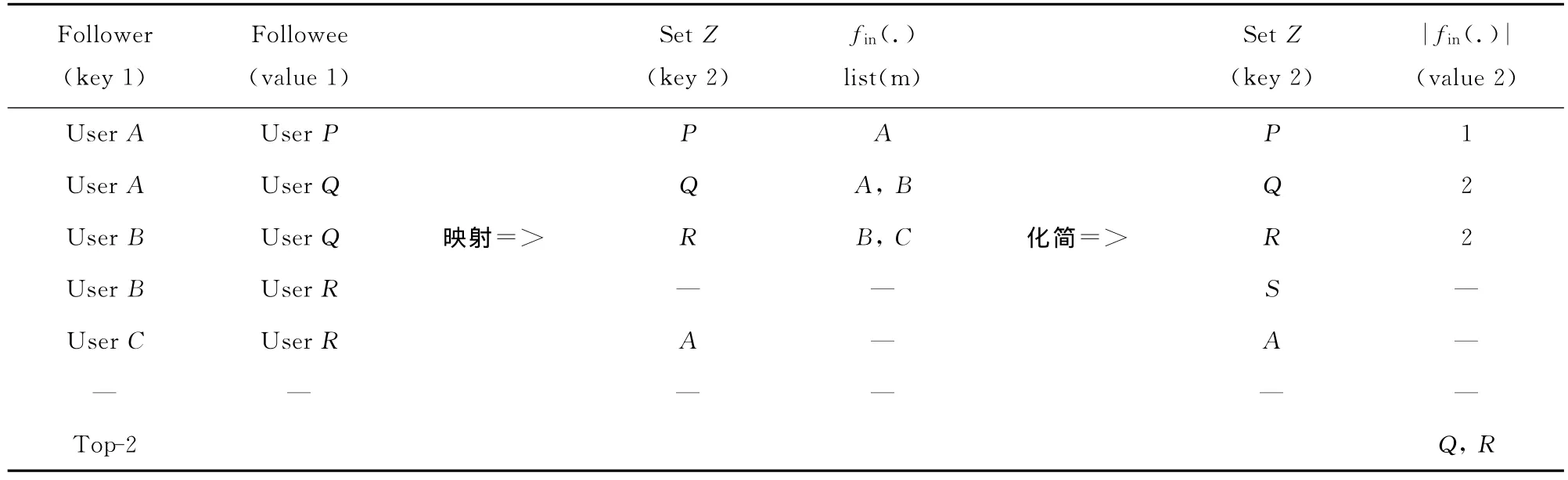
表1 映射关注和化简粉丝算法查询Top-XTab.1 Map followee &reduce follower algorithm for Top-Xquery
2)映射过程,整理建立的关系对,映射出用户集Z=[A,B,C,…,P,Q,R,…]内各用户的关注人的集合fout(X),如表1中关注User P的用户有A,关注User Q的用户有A、B等等。
3)化简过程,算出用户集Z=[A,B,C,…,P,Q,R,…]内各用户的关注人的粉丝数|fin(X)|,如表1中,User P的粉丝数为1,User Q的粉丝数为2,等等。
4)排行过程,对用户集Z=[A,B,C,…,P,Q,R,…]内各用户的关注人的粉丝数|fin(X)|进行排行,求出Top-X,如表1中X=2,即User Q和R的粉丝数多于2。
“映射关注和化简粉丝”算法已在Hadoop系统上调试,利用多台计算机实现并行计算,提高了微博平台内信息查询和化简存储的效率。与第3节介绍的“聚合-排序-删除”算法相比较,前者从平行计算的角度来提高查询效率。两个算法都说明了粉丝模型应用的方便之处。映射和化简理念在微博平台用户关系查询推广方面的应用,有待深入研究。
5 应用举例和结语
粉丝模型的提出,为在线社交网络等类型的复杂网络的用户关系描述提供了有效的逻辑模型。已实现的应用研究主要在微博平台信息查询和微博转发预测等方面,主要有4点。
1)粉丝模型和粉丝矩阵。粉丝模型[14]的提出在于描述在线网络等复杂网络的用户逻辑关系,其定义的3个函数fin(.),fout(.),fr(.)分别准确、简练地给出了用户的粉丝集、关注人集和互粉集。这些函数的反对称性、可扩展性和可组合性,使得用户间的关系更复杂,例如粉丝的粉丝(f2in(.))、粉丝的关注人(foutfin(.))以及关注人的粉丝(finfout(.))等得以进一步的描述。同时,互粉函数的对称性,也提供了互粉的互粉关系的函数(f2r(.))。这些用户关系的逻辑模型,以及第2节介绍的对粉丝模型的关系矩阵表示,为研究微博平台信息查询算法和微博转发预测方法,以及信息传播机制等的研究奠定了良好基础。
2)聚合-排序-删除的查询算法。粉丝模型的建立,为开发微博平台信息的查询算法提供了方便,聚合-排序-删除的查询算法[14]就是其中一例。在网络信息技术方面颇有影响的国际Web信息系统工程会议(The 13th International Conference on Web Information System Engineering,WISE)2012年举办以新浪微博为主题的两个竞赛项目。组织者从新浪微博收集到的12.9GB的用户关系数据和61.8GB微博信息数据为基础。第一个项目是对客户关系和微博信息数据的查询性能比赛,组织者归纳出微博关系和转发的19个查询题目,要求参赛者开发优化算法,使用由中国IMC公司推出的BSMA性能测试工具,对这些查询进行通过量、延时和数据规模等3项指标的性能分析。
本文第3节介绍的“聚合-排序-删除”算法,就是应用粉丝模型,开发出来的微博平台优化算法,实现此类组查询,取得数据规模单项竞赛并列第1名的成绩[12]。
3)微博转发预测。2012年WISE的第2个竞赛项目是预测新浪微博与6个社会事件有关的33个微博的转发情况。主办方界定一个时间戳,并给出在此时间前用户对这些微博的原始资料。参赛者应根据发表在30天内的这33个微博,预测原微博被转发的次数和原微博可能被阅读的次数。一次微博转发行为后,微博可能被阅读数定义为转发该微博的用户粉丝数。原微博可能被阅读的总次数是所有转发行为后该微博可能被阅读数之和。
这两个数字的计算取决于微博转发的若干特性、粉丝模型以及相关优化算法,由此建立预测模型,如基于条件随机场模型。具体预测方法和结果分析,参见文献[20]。
4)映射关注和化简粉丝算法。“映射关注和化简粉丝”算法的功能在于,首先从原数据集中映射出具有某特性用户间的关注关系,然后在所得到的粉丝集(fin(.))里边通过化简算出Top-X用户来。对该算法的检验,是使用由H.Kwak团队从Twitter收集的26GB用户关系数据[16]和J.Yang等提供的75GB Tweets数据[21]。在Hadoop系统的并行联机计算环境支持下,算法的信息查询和化简存储性能明显优于传统方式。该案例是映射和化简方法在微博大数据研究的首次尝试,也进一步验证了粉丝模型应用的潜在能力。
本文系TransLab实验室2011年以来对在线社交网络,特别是对微博和Twitter研究的综合报告,涉及到的社交网络的用户间关系和行为的逻辑描述和相关计算方法。鉴于网络结构的复杂性、信息查询的艰巨性,这些研究工作引进了粉丝模型、映射和化简等新理念和Hadoop数据管理新技术等,使得在线社交网络的研究方法和结果引人注目和富有挑战。本文描述的模型和算法虽然通过实际案例分析得到了初步检验,但理论分析需要进一步加强,亦希望得到同行评议和指正。
[1]Sun Y,Han J,Aggarwal C C,et al.When will it happen?—relationship prediction in heterogeneous information networks[C]//Proceedings of the fifth ACM international Conference on Web Search and Data Mining.New York,USA:ACM,2012:663-672.
[2]Sun Z,Wang H,Wang H,et al.Efficient subgraph matching on billion node graphs[J].Proc VLDB Endow,2012,5(9):788-799.
[3]Zhao X,Sala A,Wilson C,et al.Multi-scale dynamics in a massive online social network[C]//Proceedings of the 2012 ACM Conference on Internet Measurement Conference.New York,USA:ACM,2012:171-184.
[4]Kang U,Chau D H,Faloutsos C.Pegasus:Mining billion-scale graphs in the cloud[C]//2012IEEE International Conference on Acoustics,Speech and Signal Processing(ICASSP).Kyoto,2012:5341-5344.
[5]Kim M,Leskovec J.Multiplicative attribute graph model of real-world networks[J].Internet Mathematics,2012,8(1/2):113-160.
[6]方锦清,汪小帆,郑志刚,等.一门崭新的交叉科学:网络科学(下篇)[J].物理学进展,2008,27(4):361-448.
Fang Jinqing,Wang Xiaofan,Zheng Zhigang,et al.New interdisciplinary science:network science(II)[J].Progress in Physics,2008,27(4):361-448.
[7]Tang J,Zhang J,Yao L,et al.ArnetMiner:extraction and mining of academic social networks[C]//Proceedings of the 14th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.New York,USA:ACM,2008:990-998.
[8]Zhou A,Qian W,Ma H.Social media data analysis for revealing collective behaviors[C]//Proceedings of the 18th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.New York,USA:ACM,2012:1402-1402.
[9]段磊,唐常杰,杨宁,等.干预规则挖掘的概念、任务与研究进展[J].计算机学报,2011,34(10):1831-1843.
Duan Lei,Tang Changjie,Yang Ning,et al.Concepts,tasks and research advances of intervention rule ming[J].Chinese Journal of Computers,2011,34(10):1831-1843.
[10]Cheng X,Shen H.Uncovering the community structure associated with the diffusion dynamics on networks[J].Journal of Statistics Mechanics,2010(4):4-24.
[11]杨涵新,汪秉宏.复杂网络上的演化博弈研究[J].上海理工大学学报,2012,34(2):166-171.
Yang Hanxin,Wang Binghong.A review about the evolutionary games on complex networks[J].Journal of University of Shanghai for Science and Technology,2012,34(2):166-171.
[12]LüL,Zhou T.Link prediction in complex networks:a survey[J].Physica A:Statistical Mechanics and Its Applications,2011,390(6):1150-1170.
[13]Cheng D,Qi H,Zhao Y.Analysis and control of general logical networks-an algebraic approach[J].Annual Reviews in Control.2012,36(1):11-25.
[14]Sandes E F O de,Li W G,Melo A C M A de.Logical model of relationship for online social networks and performance optimizing of queries[G]//Wang X S,Cruz I,Delis A,et al.Web Information Systems Engineering-WISE 2012.New York:Springer Berlin Heidelberg,2012:726-736.
[15]Unankard S,Chen L,Li P,et al.On the prediction of re-tweeting activities in social networks—a report on WISE 2012 challenge[G]//Wang X S,Cruz I,Delis A,et al.Web Information Systems Engineering-WISE 2012.Springer Berlin Heidelberg,2012:744-754.
[16]Kwak H,Lee C,Park H,et al.What is twitter,a social network or a news media?[C]//Proceedings of the 19th International Conference on World wide web.New York,USA:ACM,2010:591-600.
[17]Ghemawat S,Dean J.MapReduce:simplified data processing on large clusters[C]//Proceedings of Symposium on Operating System Design and Implementation(OSDI 2004).San Francisco,California,USA:137-150.
[18]Foley J D.Computer Graphics:Principles and Practice[M].New York:Addison-Wesley Professional,1996.
[19]李伟钢.复杂系统结构有序度——负熵算法[J].系统工程理论实践,1988,8(4):15-22.
Li Weigang.Negative Entropy-the sequence of the complex system structure[J].System Engineering-Theory &Practice,1988,8(4):15-22.
[20]Junior J,Almeida L,Modesto F,et al.An investigation on repost activity prediction for social media events[G]//Wang X S,Cruz I,Delis A,et al.Web Information Systems Engineering-WISE 2012.Springer Berlin Heidelberg,2012:719-725.
[21]Yang J,Leskovec J.Patterns of temporal variation in online media[C]//Proceedings of the Fourth ACM international Conference on Web Search and Data Mining.New York,USA:ACM,2011:177-186.
Logical Model and Parallel Querying in Online Social Networks
LI Wei-gang,ZHENG Jian-ya
(TransLab,Department of Computer Science,University of Brasilia,Brasilia 70910-900,Brazil)
Based on a thorough literature review in the related field,this paper presents some meaningful but challenging research topics in OSNs.The logical model(Follow Model)is introduced.To present the basic relationships between the users,the Relationship Committed Adjacency Matrix (Follow Matrix)is put forward.Then applying this logical model to show its effect,the Aggregation-Ranking-Delete algorithm is presented to rank the Top-X in OSNs.The paper further puts the new way of computing,combining the concept of MapReduce,into the parallel querying,which further leads to Map Followee and Reduce Follower algorithm implemented in Hadoop system.Follow Model and related algorithms are applied with the data collected from Sina Weibo(74.7GB)and Twitter(101GB)for the multi-constraint querying and retweeting prediction.The results demonstrate that the new solution with parallel paradigms in Hadoop has significantly improved the effect with the information storage adequately reduced and the computing power greatly increased.
complex system;parallel computing;Micro-blog;information query;MapReduce;online social networks;
N945
A
1672-3813(2013)02-0077-11
2013-03-20
巴西科学技术发展委员会(CNPq,304058/2010-6,478039/2012-3)
李伟钢(1958-),男,河南南阳人,博士,副教授,主要研究方向为航空交通模型与人工智能。
(责任编辑 耿金花)

