加权无标度网络级联抗毁性研究
王甲生,吴晓平,陈永强
(海军工程大学信息安全系,武汉 430033)
加权无标度网络级联抗毁性研究
王甲生,吴晓平,陈永强
(海军工程大学信息安全系,武汉 430033)

通过引入一种改进的非线性负载容量模型,对加权无标度网络的级联抗毁性进行了深入研究。采用标准化崩塌规模为度量指标,在局部加权负载重分配准则下,对权重系数、容量参数以及网络密度等参量对网络级联抗毁性的影响进行了数值仿真模拟。结果表明,网络的级联抗毁性随着权重系数θ的增大而降低,在θ≤0.3时网络具有较强的抗毁性,这与线性模型中的结论是截然不同的;网络的级联抗毁性随着容量参数的增大而增强,且在权重系数确定的情况下,存在最优参数组合使得网络具有最强的级联抗毁性。最后,对成本和性能约束下加权无标度网络的级联抗毁性进行了定量分析。
加权无标度网络;抗毁性;级联失效;负载容量模型;权重系数
0 引言
复杂网络作为复杂性科学的一个重要研究领域,近年来受到数学、物理学、生物学、社会学、信息科学以及军事和经济等各学科领域研究人员的广泛关注[1]。随着复杂网络研究的兴起,其抗毁性研究也备受关注,特别是一些现代社会赖以生存的重要基础设施网络,如电力网络、金融网络、交通网络等,其抗毁性研究显得尤为迫切。复杂网络的级联抗毁性是复杂网络抗毁性研究的一个重要方面,是指当网络中节点发生故障或被攻击时,在节点容量有限的情况下,网络上的负载进行重新分配使得相关节点上的负载超过其容量而失效的动态过程,可能导致部分网络故障甚至整个网络的崩溃[2]。在现实世界中很多网络灾难都可以归结为这类级联崩溃问题,比如2012年7月发生的印度大停电事故,同样的问题也存在于通信网、交通网、因特网等网络系统之中。
复杂网络上的级联抗毁性研究近年来得到了很大关注。Motter等[2]首次研究了不同类型网络中的级联失效,通过引入一个负载容量线性模型,发现异构网络中级联失效对选择性攻击具有敏感性。Crucitti等[3]提出了一种节点和边的混合动态相继故障模型,并采用级联失效后网络的平均加权效率度量级联失效的后果。Schafer等[4]提出了一种增加网络级联失效抗毁性的设计方法,并通过减少网络总负载来提高网络抗毁性。Wang W X等[5]研究了加权复杂网络对级联失效的鲁棒性与权重分布的关系,结果表明存在最优权重分布使网络具有最强的鲁棒性。Mirzasoleiman B[6]等研究了加权网络对于级联失效的鲁棒性,并在电力网、AS级Internet网络、铁路网以及航空网上进行了验证,结果表明赋权模型为端节点介数乘积的网络具有最强的鲁棒性。LI S D[7]等研究了无标度网络、WS小世界网络和ER随机网络由最大负载攻击(HL)和随机攻击(RA)引起的网络的级联失效问题。Babaei M等[8]研究了模块化小世界网络对于级联失效的鲁棒性,研究表明模块内部连接对于网络鲁棒性具有重要作用,且模块化程度越高的网络其鲁棒性越差。DOU B L[9]等提出了一种非线性负载容量模型,并在BA无标度网络、ER随机网络、AS级Internet网络以及电力网上进行了仿真。朱涛等[10]研究了指挥控制级联失效模型,并就不同条件下指挥控制的级联失效特征变化情况进行了定量分析。李勇等[11]建立了度均匀随机分布的网络模型和负载局部扩展的级联失效抗毁性模型,并运用多维分支过程方法求解网络级联失效的临界值。任俊亮等[12]建立了一个无尺度网络的相继故障模型,该模型采用基于节点剩余容量的负载重分配策略能较充分地利用网络资源。王威等[13]提出了基于随机行走介数的级联失效模型。
在实际网络的级联抗毁性研究中,一个关键的问题是合理设定节点和边的容量,使之尽可能符合实际。另一方面,由于实际网络的构建也是需要考虑成本的,因此也需要设计合理的负载容量模型以抵御级联失效。文献[14]研究了大规模基础设施网络的负载与容量之间的关系,发现负载与容量之间呈现出非线性关系,这一结论与以往研究中[2,5-8,10,12-13]假设的负载容量模型是截然不同的。因此,本文通过引入一种改进的非线性负载容量模型,在局部加权负载重分配准则下,采用数值仿真的方法研究了加权标度网络权重系数、容量参数以及网络密度等对网络级联抗毁性的影响,定量分析了成本和性能约束下的加权无标度网络级联抗毁性。
1 加权复杂网络级联失效分析
1.1 加权复杂网络
加权复杂网络已经成为复杂网络的一个重要的研究方向,可以用图G=(V,E)来表示,假设G是一个无向连通图,有n个节点和m 条带有权重的边,节点集V= (v1,v2,…,vn),边集E= (e1,e2,…,em)。一般用权重邻接矩阵W= (wij)n×n表示加权网络权重,wij表示节点vi与vj连接的边的权重,当网络中各条边的权值都相同时,加权网络即退化为无权网络。
把一个实际系统抽象为加权网络的过程并不是平庸的,以往的权重模型主要有YJBT模型、AK模型以及BBV模型等。本文考虑了一种将无权网络的性质转化为边权的赋权模型,边权与其两个端节点的度相关[6,15]。边权的赋予方式为:假设网络中边eij连接的两个节点vi与vj的度值分别为ki和kj,那么该边的权重为wij=wji= (kikj)θ,其中θ(θ>0)为一个可调的权重系数,用于描述边权与节点度之间的相互关系。这种边权的赋予方式是有实证数据作支撑的,在目前加权网络的研究中得到了广泛的应用。权重系数θ决定了加权复杂网络边的非同质性,当θ=0时,对应的边权w=1,表明边权与节点度之间没有关联,加权网络退化为无权网络;当θ>0时,加权网络的特性由权重来刻画,且θ越大则各边之间的差异越大。
1.2 级联失效
假设加权复杂网络的级联失效是由一个微小的初始攻击触发的,比如切除网络中的任意一条边。那么,在局部加权的负载重分配准则[5-6]下,这条断边上的负载将分配给其端节点相连的邻边,且邻边接收到的负载正比于边的权重。与以往的模型一样,加权网络中每条边所能处理的最大负载称为该边的容量,一般来说边的容量是有限的。
负载的重分配和有限容量使得一个节点的失效足以导致整个网络的崩溃。在初始状态下,加权网络处于一个稳定的状态,每条边上的负载均小于其容量。任意一条边的移除将改变之前的平衡状态,由此引发的负载重分配可能导致其它相连边的失效,这些边的失效又可能导致相连边的失效,直到网络中每条边的负载都不超过其容量为止。
P.Holme等[16]的研究指出,复杂网络中边的介数与该边的端节点的度的乘积形式是正相关的。因此,可以合理地设定在边eij移除之前,如果其没有接收到额外的负载Δwij,那么该边上的负载就等于该边的权重wij。
2 改进的负载容量非线性模型
在实际网络中,边的容量是受成本和可用资源约束的。因此,在以往的研究工作中,复杂网络中边的容量被设定为正比于其权重,比如C=Tw,其中常数T(T>1)为临界系数,w为边的权重;或者C= (1+a)L,其中常数a为容忍系数,L为边的初始负载。然而,D H Kim等通过对航空运输网络、公路交通网络、电力网络及路由器网络的实证研究发现,实际网络中容量较小的节点(边)反而有较大的未使用容量,即负载与容量之间呈现出非线性关系,表明以上假设的负载容量线性模型与现实是不相符的。
据此,本文给出了一个改进的负载容量非线性模型,将加权网络中边的容量表示为C=L+βLα,其中α(α>0)和β(β>0)为容量参数。该模型包含两个可变参数,灵活性更高,且当α=1时模型即退化为线性模型。图1给出了改进负载容量模型与线性模型C= (1+a)L在对数坐标系中的比较,图中灰色实线表示改进的负载容量模型,虚线表示线性模型,黑色实线为容量等于负载的参考线。
由图1可以看出,以往的线性模型中容量是正比于负载的,改进的负载容量模型在负载较小时空闲容量较大,负载较大时空闲容量反而较小,与文献[14]中对实际网络的研究结论一致。
另外,在级联失效发生后,本文采用崩塌规模Sij来表示切断边eij触发的级联失效对网络造成的破坏程度,崩塌规模Sij即网络中失效边的数量。为了衡量整个网络的级联抗毁性,对崩溃规模进行标准化,采用标准化崩塌规模SN来表示依次切断每条边后对网络造成的平均破坏程度。S=∑ijSij/N,其中N为网络中边的数量。标准化崩溃规模SN可以看作是复杂网络面对随机失效的级联抗毁性的平均度量。
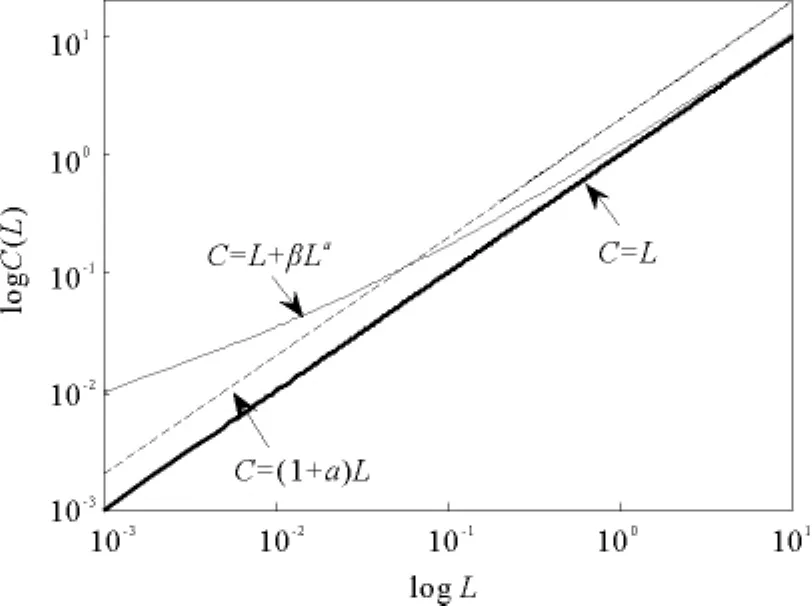
图1 线性与非线性负载容量模型Fig.1 The linear and nonlinear load-capacity model
3 加权无标度网络级联抗毁性仿真分析
现实生活中的许多网络如因特网、航空运输网、电力网等都具有明显的无标度特性。为了更好地理解实际网络特征参数与级联抗毁性之间的关系,本文研究了加权无标度网络的抗毁性。首先,构建加权无标度网络,其初始节点数n0=5,m=4,节点总数N=5 000,网络的构建依赖于择优吸附机制。然后,依据1.1节中的赋权方式对BA网络进行赋权,其中权重系数θ在[0,2]之间取值。当θ=0.5时,加权无标度网络的负载分布如图2所示,呈现出幂律分布的特性。
加权无标度网络的级联抗毁性与权重系数θ、容量参数α和β等是密切相关的,其级联抗毁性分析较为复杂。本节分别研究加权无标度网络级联抗毁性与权重系数、容量参数以及网络密度等网络参数的关系,并定量分析了成本和性能约束下的级联抗毁性。
3.1 容量参数固定的抗毁性仿真
加权无标度网络中边的容量由α和β两个参数共同决定的,在对实际网络进行研究的基础上,获得容量参数的近似值。设定α=0.45,β=0.20,加权无标度网络级联抗毁性与权重系数θ的关系如图2所示,仿真结果为10次计算的平均值。
由图3可知,在容量参数固定的情况下,标准化崩塌规模SN随着权重系数θ的增大不断增大,即网络的抗毁性随θ增大而不断降低。当θ<0.4时,SN接近于0,网络表现出最强的抗毁性。然而当θ≥0.4时,SN迅速增大,且当θ>0.8时,网络几乎全盘崩溃。这一结果与对文献[5]的进一步的研究结论完全不同。Wang W X等采用线性负载容量模型,其研究工作侧重于控制级联失效的开始及传播,对于控制任意结构加权无标度网络级联失效的发生及失效范围具有重要指导意义。然而,进一步的研究表明,随着级联失效范围的扩大,标准化崩塌规模SN与阈值T的关系是单调的。在线性负载容量模型中,网络抗毁性与阈值T的关系如图4所示,仿真结果为10次计算的平均值。

图2 加权无标度网络的负载分布曲线Fig.2 Load distribution of weighted scale-free networks
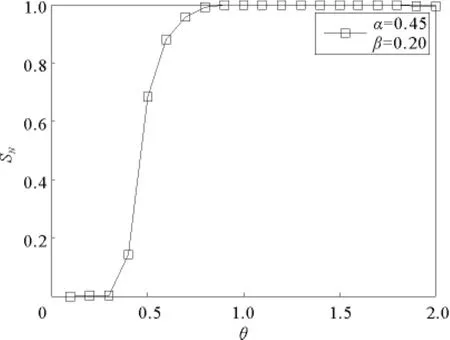
图3 网络抗毁性与权重系数的关系曲线Fig.3 Invulnerability as a function of weight coefficient
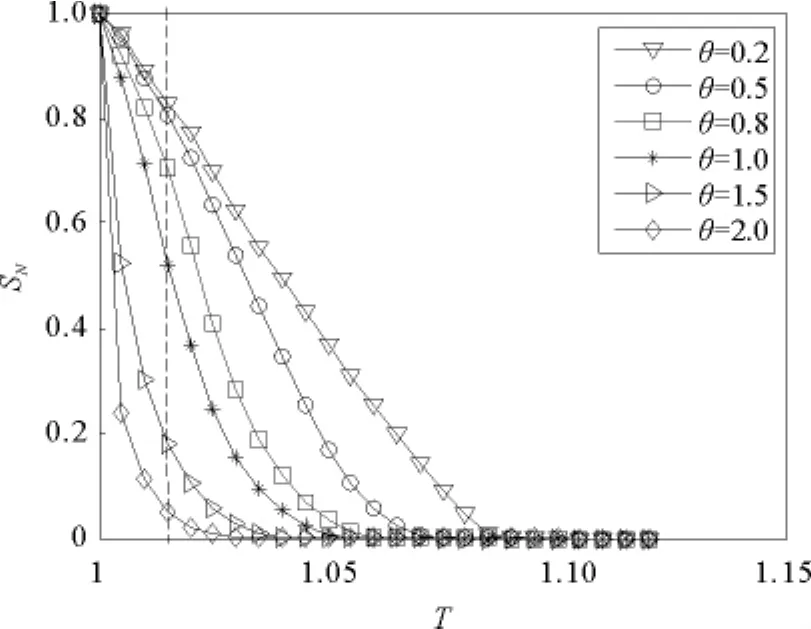
图4 线性模型中抗毁性与阈值T的关系曲线Fig.4 Relationship between invulnerability and the threshold T
由图4可以看出,在线性负载容量模型中,随着级联失效规模的扩大,对于确定的阈值T0,权重系数θ越大,标准化崩塌规模SN就越小,加权无标度网络的级联抗毁性越强。这与本文上述得出的结论是截然不同的,这种差异正是由于负载容量之间的非线性关系造成的。
3.2 不同容量参数的抗毁性仿真
D H Kim等对实际网络的实证研究也发现,不同复杂网络中负载容量的关系曲线是不同的。为此,本文研究了不同容量参数下加权无标度网络的级联抗毁性。图5和图6分别为加权无标度网络级联抗毁性与容量参数α和β的关系曲线,仿真结果为10次计算的平均值。

图5 网络抗毁性随容量参数α的变化曲线Fig.5 Invulnerability as a function of parameterα

图6 网络抗毁性随容量参数β的变化曲线Fig.6 Invulnerability as a function of parameterβ
在图5中,参数β=0.20。由图5a可知,对于给定的α值,随着θ的不断增大,SN不断增大,网络的级联抗毁性不断降低。对于给定的θ值,随着α的不断增大,网络的级联抗毁性不断增强,θ=0.5时的情况如图5b所示。在图6中,参数α=0.45。参数β对网络级联抗毁性的影响与α类似。对于给定β值,随着θ的不断增大,网络的级联抗毁性不断降低。对于给定的θ值,随着β的不断增大,网络的级联抗毁性不断增强,如图6b所示。随着参数α和β的不断增大,网络的级联抗毁性不断增强,这与直观上的认识是一致的。
从图5和图6也可以看出,不同容量参数的网络在θ较小(θ≤0.3)时,表现出较强的抗毁性,随着θ的进一步增大,网络抗毁性急剧降低。另外,随着α和β的增大,网络抵抗级联失效的空闲容量ΔC=βLα也不断增大,网络成本也进一步增加。因此,从控制成本的角度考虑,可以减小网络的权重系数,随后根据实际需要对容量参数进行调节,使网络的级联抗毁性最强。
3.3 不同网络密度对抗毁性的影响
网络密度对加权网络的级联抗毁性也存在一定影响。网络密度表现为平均度〈k〉,网络密度与网络级联抗毁性的关系曲线如图7所示,仿真结果为10次计算的平均值。
在图7中,容量参数α=0.45,β=0.20。由图7a可知,给定〈k〉的情况下,随着权重系数θ的不断增大,网络的级联抗毁性先降低,随后又略有增强。对于给定的θ值,网络的级联抗毁性与〈k〉的关系如图7b所示。由图7b可知,在θ=0.5的情况下,网络的级联抗毁性在〈k〉=2时最强,在〈k〉=4时最差,随着〈k〉的继续增大有所增强。另外,由图7a可以看出,不同密度的加权无标度网络在θ<0.3时级联失效规模较小,而当θ≥0.3时级联失效传播的速度迅速加快。从控制级联失效传播范围的角度考虑,可以采取的方法是首先减小权重系数,进而根据需要对网络密度进行一定调整。
3.4 考虑成本与性能的抗毁性优化分析
在实际网络的抗毁性研究中,通常人们比较关心的是如何在保持成本一定的情况下,设计抗毁性最优的网络[17]。前面给出了加权无标度网络级联抗毁性与各参数的定性关系,下面从定量的角度给出加权无标度网络抗毁性的优化分析模型。
加权无标度网络的级联抗毁性可以表示为网络鲁棒性与网络成本的函数。
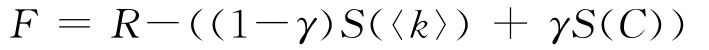
其中,F为加权无标度网络级联抗毁性目标函数。R为网络鲁棒性,用最大连通子图的相对大小来表示,R=G′/G,G′和G分别表示级联失效发生前后的最大连通子图大小。S为成本,与网络密度〈k〉和边容量C相关,表示为S(〈k〉)和S(C)。S(〈k〉)=m/n0,m 为平均连接数,n0为无标度网络的初始节点数。S(C)=∑ijΔC/ΣijL,L为初始负载,S(C)为网络的相对增加成本。γ为加权系数,表示网络边容量决定的网络成本的重要性,通过调节γ,可以均衡容量成本和密度成本对网络抗毁性的影响。本文重点考虑容量成本对网络级联抗毁性的影响,取γ=1。成本和性能约束下,加权无标度网络的级联抗毁性与各参数的关系曲线如图8所示。

图7 不同网络密度与级联抗毁性的关系曲线Fig.7 Invulnerability as a function of parameter〈k〉
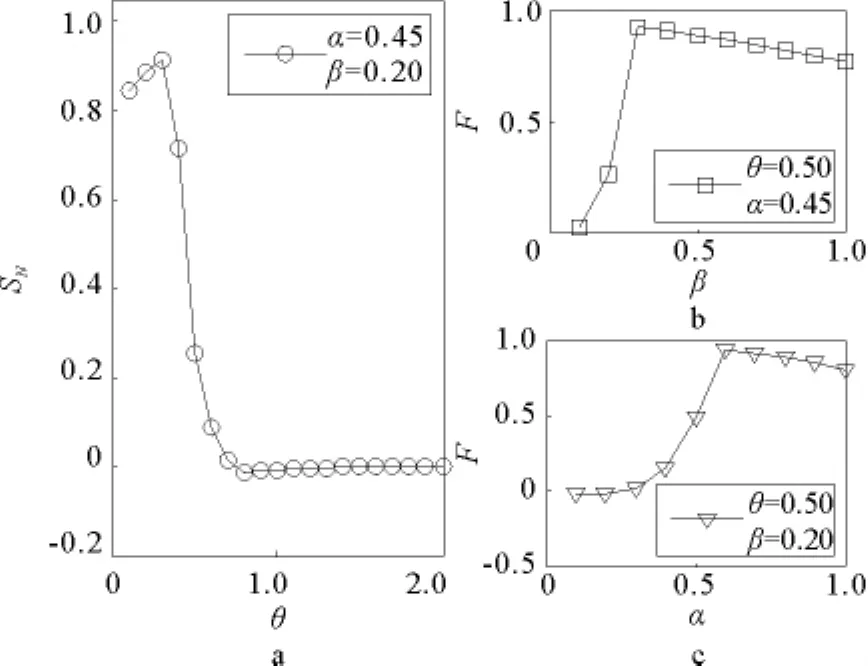
图8 成本和性能约束下级联抗毁性与α,β和θ的关系曲线Fig.8 Invulnerability as functions ofα,βandθconsidering cost and network performance
由图8a可知,在确定容量参数α和β的情况下,网络在θ∈[0.1 0.3]时具有较强的级联抗毁性,且在θ=0.3时抗毁性最强,随后又迅速降低,到θ≥0.7时网络全盘崩溃。在图8b和c可知,网络的级联抗毁性随着α和β的逐渐增大呈现出先增强后减弱的趋势,也就是说在确定权重系数θ的情况下,网络存在最优级联抗毁性,以θ=0.5为例,网络在α=0.60,β=0.20时抗毁性最强。
由图3~图8的仿真结果可以得出如下结论,在非线性负载容量模型条件下:
1)加权无标度网络的级联抗毁性随着权重系数θ的增大而降低,当θ≤0.3时网络具有较强的抗毁性,当θ>0.3时级联抗毁性迅速降低,而当θ>0.8时网络接近全盘崩溃,这与文献[5]中关于线性模型的结论是完全相反的。
2)加权无标度网络的级联抗毁性随着容量参数α和β的增大而增强,这与直观上的认识是一致的。然而,容量参数的增大也在一定程度上增加了网络成本。从控制成本的角度考虑,首要是减小网络的权重系数,随后根据需要对容量参数进行调节,使得网络的级联抗毁性最强。
3)在成本和抗毁性约束下,加权无标度网络的抗毁性在权重系数θ≤0.3时较强,且在权重系数θ确定的情况下,通过调节容量参数α和β,加权无标度网络存在最优的级联抗毁性。
由此可以看出,本文的研究成果能够从整体上把握加权负载网络的级联抗毁性状况,且能灵活调节参数以获取最大的级联抗毁性。
4 结论
本文通过引入改进的非线性负载容量线性模型,对加权无标度网络的级联抗毁性进行了深入研究。结果表明,加权无标度网络的级联抗毁性随着权重系数的增大而降低,随容量参数的增大而增强,且在权重参数固定的情况下存在最优参数组合使得网络具有最强抗毁性。研究成果能够为实际网络的抗毁性优化设计提供一定的参考和借鉴。另外,本文的研究可以看作是加权无标度网络面对随机失效的级联抗毁性,实际上网络面临的攻击更多的是蓄意攻击,因此加权无标度网络面对基于高负载节点或蓄意攻击的级联抗毁性问题将是下一步研究重点。
[1]陈关荣,陈增强,吕金虎.复杂网络科学与工程的研究进展[J].系统工程学报,2010,25(6):723-724.
Chen Guanrong,Chen Zengqiang,LüJinhu.Advances on complex networks science and engineering[J].Journal of Systems Engineering,2010,25(6):723-724.
[2]Motter A E,Lai Y C.Cascade-based attacks on complex networks[J].Phys Rev E,2002,66(6):065102.
[3]Crucitti P,Latora V,Marchiori M.Model for cascading failures in complex networks[J].Phys Rev E,2004,69(4):045104.
[4]Schafer M,Scholz J,Greiner M.Proactive robustness control of heterogeneously loaded networks[J].Phys Rev Lett,2006,96(10):108701.
[5]Wang W X,Chen G R.Universal robustness characteristic of weighted networks against cascading failure[J].Phys Rev E,2008,77(2),026101.
[6]Mirzasoleiman B,Babaei M,Jalili M,et al.Cascaded failures in weighted networks[J].Phys Rev E,2011,84(4):046114.
[7]Li S D,Li L X,Yang Y X,et al.Revealing the process of edge-based-attack cascading failures[J].Nonlinear Dyn.,2012,69(3):837-845.
[8]Babaei M,Ghassemieh H,Jalili M.Cascading failure tolerance of modular small-world networks[J].IEEE Transactions on Circuits and Systems-II:Express Briefs,2011,58(8):527-531.
[9]Dou B L,Wang X G,Zhang S Y.Robustness of networks against cascading failures[J].Physica A,2010,389(11):2310-2317.
[10]朱涛,常国岑,张水平,等.基于复杂网络的指挥控制级联失效模型研究[J].系统仿真学报,2010,22(8):1817-1820.
Zhu Tao,Chang Guocen,Zhang Shuiping,et al.Reseatch on model of cascading failure in command and control based on complex networks[J].Journal of System Simulation,2010,22(8):1817-1820.
[11]李勇,吴俊,谭跃进.物流保障网络级联失效临界抗毁性[J].系统仿真学报,2012,24(5):1030-1034.
Li Yong,Wu Jun,Tan Yuejin.Critical invulnerabiity study for cascading failure of tactical logistics networks[J].Journal of System Simulation,2012,24(5):1030-1034.
[12]任俊亮,申卯兴,仝蕊,等.无尺度网络中降低相继故障规模的策略研究[J].计算机工程与应用,2011,47(33):82-84.
Ren Junliang,Shen Maoxing,Tong Rui,et al.Study of reducing size of cascading failures in scale-free network[J].Computer Engineering and Applications,2011,47(33):82-84.
[13]王威,狄鹏,胡斌.基于随机行走介数的级联失效模型[J].系统工程与电子技术,2012,34(9):1914-1917.
Wang Wei,Di Peng,Hu Bin.Cascading failure model based on random-walk betweenness[J].Systems Engineering and Electronics,2012,34(9):1914-1917.
[14]Kim D H,Motter A E.Resource allocation pattern in infrastructure networks[J].J Phys A:Math Theor,2008,41(22):224019.
[15]Zhang Y C,Zhou S,Zhang Z Z,et al.Traffic fluctuation on weighted networks[J].IEEE Circuits and Systems,2012,12(1):33-44.
[16]Holme P,Kim B J,Yoon C N,et al.Attack vulnerability of complex networks[J].Phys Rev E,2002,65(5):056109.
[17]Li P,Wang B H,Sun H,et al.A limited resource model of fault-tolerant capability against cascading failure of complex network[J].Eur Phys J B,2008,62(1):101-104.
Invulnerability of Weighted Scale-Free Networks Against Cascading Failure
WANG Jia-sheng,WU Xiao-ping,CHEN Yong-qiang
(Department of Information Security,Naval University of Engineering,Wuhan 430033,China)
To solve the problem of invulnerability analysis of weighted scale-free networks against cascading failure,an improved nonlinear load-capacity model is introduced.The normalized avalanche size is adopted as the measurement of invulnerability,and under the rule of local weighted load redistribution,the influence of weight coefficient,capacity parameters and density of the network on invulnerability of weighted scale-free networks against cascading failure is investigated by numerical simulation.The results demonstrate that the smaller of the weight coefficientθ,the better of the invulnerability,especially whenθ≤0.3,which contrasts with the conclusion drawn from the linear model.In addition,the larger of the capacity parameters,the better of the invulnerability.And moreover,when the weight coefficient is fixed,there exists an optimal combination of the capacity parameters which ensures that the weighted networks reach the strongest invulnerability level.Finally,the qualitative analysis of invulnerability of weighted scale-free networks against cascading failure under the restrictions of cost and performance is presented.
weighted scale-free networks;invulnerability;cascading failure;load-capacity model;weight coefficient
N949
A
1672-3813(2013)02-0013-07
2012-08-24
国家自然科学基金(71171198,61100042);湖北省自然科学基金(2011CDB052)
王甲生(1984-),男,陕西渭南人,博士研究生,主要研究方向为复杂系统分析建模与仿真。
(责任编辑 李进)

